\( \newcommand{\C}{\mathbb{C}} \newcommand{\R}{\mathbb{R}} \newcommand{\F}{\mathbb{F}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\D}{\mathbb{D}} \def\H{\mathbb{H}} \newcommand{\mult}{\mathop{\mathrm{mult}}\nolimits} \renewcommand{\L}{{\mathcal{L}}} \newcommand{\B}{{\mathcal{B}}} \newcommand{\A}{{\mathcal{A}}} \newcommand{\M}{{\mathcal{M}}} \renewcommand{\S}{{\mathcal{S}}} \newcommand{\T}{{\mathcal{T}}} \newcommand{\dist}{\mathop{\mathrm{dist}}\nolimits} \newcommand{\Null}{\mathop{\mathrm{null}}\nolimits} \newcommand{\Span}{\mathop{\mathrm{span}}\nolimits} \newcommand{\re}{\mathop{\mathrm{Re}}\nolimits} \newcommand{\Ind}{\mathop{\mathrm{Ind}}\nolimits} \newcommand{\Res}{\mathop{\mathrm{Res}}\nolimits} \newcommand{\esssup}{\mathop{\mathrm{ess\,sup}}} \newcommand{\im}{\mathop{\mathrm{Im}}\nolimits} \newcommand{\Int}{\mathop{\mathrm{int}}\nolimits} \newcommand{\graph}{\mathop{\mathrm{graph}}\nolimits} \newcommand{\arccot}{\mathop{\mathrm{arccot}}\nolimits} \newcommand{\myallowbreak}{} \newcommand\p[2][]{\frac{\partial #1}{\partial #2}} \newcommand\sgn{\mathop{\mathrm{sgn}}\nolimits} \newcommand\cl{\mathop{\mathrm{cl}}\nolimits} \newcommand\abs[1]{|#1|} \)
MATH 55203–55303
Theory of Functions of a Complex Variable I–II
Fall 2025–Spring 2026
(Spring) SCEN 322, MWF 2:00–2:50 p.m.
Next class day: Monday, March 16, 2026
The set of complex numbers is \(\R ^2\), denoted \(\C \). (In this class, you may use everything you know about \(\R \) and \(\R ^2\)—in particular, that \(\R ^2\) is an abelian group and a normed vector space.)
If \((x,y)\) is a complex number, then \(\re (x,y)=x\) and \(\im (x,y)=y\).
If \((x,y)\) and \((\xi ,\eta )\) are two complex numbers, we define
Show that multiplication in the complex numbers is commutative.
Let \((x,y)\) and \((\xi ,\eta )\) be two complex numbers. Then\begin{align*} (x,y)\cdot (\xi ,\eta )&=(x\xi -y\eta ,x\eta +y\xi ),\\ (\xi ,\eta )\cdot (x,y)&=(\xi x-\eta y,\xi y+\eta x). \end{align*}Because multiplication in the real numbers is commutative, we have that
\begin{align*} (\xi ,\eta )\cdot (x,y)&=(x\xi -y\eta ,y\xi + x\eta ). \end{align*}Because addition in the real numbers is commutative, we have that
\begin{align*} (\xi ,\eta )\cdot (x,y)&=(x\xi -y\eta , x\eta +y\xi )=(x,y)\cdot (\xi ,\eta ) \end{align*}as desired.
This notion of addition and multiplication makes the complex numbers a ring—thus, multiplication is also associative and distributes over addition.
What is the multiplicative identity?
Let \(r\) be a real number. Recall that \(\C =\R ^2\) is a vector space over \(\R \), so we can multiply vectors (complex numbers) by scalars (real numbers). Is there a complex number \((\xi ,\eta )\) such that \(r(x,y)=(\xi ,\eta )\cdot (x,y)\) for all \((x,y)\in \C \)?
If \(x\), \(y\) are real numbers, what complex number is \(x+iy\)?
If \(z=x+iy\) for \(x\), \(y\) real, what are \(\re z\) and \(\im z\)?
If \(z\in \C \) and \(r\) is real, what are \(\re (zr)\) and \(\im (zr)\)?
If \(z\), \(w\in \C \), what are \(\re (z+w)\), \(\im (z+w)\) in terms of \(\re z\), \(\re w\), \(\im z\), and \(\im w\)?
If \(z\), \(w\in \C \), what are \(\re (zw)\), \(\im (zw)\) in terms of \(\re z\), \(\re w\), \(\im z\), and \(\im w\)?
The conjugate to the complex number \(x+iy\), where \(x\), \(y\) are real, is \(\overline {x+iy}=x-iy\).1
If \(z\) and \(w\) are complex numbers, show that \(\bar z+\overline w=\overline {z+w}\).
Show that \(\bar z\cdot \overline {w}=\overline {zw}\).
Write \(\re z\) and \(\im z\) in terms of \(z\) and \(\bar z\).
Show that \(z\bar z\) is always real and nonnegative. If \(z\bar z=0\), what can you say about \(z\)?
If \(z\) is a complex number with \(z\neq 0\), show that there exists another complex number \(w\) such that \(zw=1\). Give a formula for \(w\) in terms of \(z\). We will write \(w=\frac {1}{z}\).
\(z\bar z\) is a positive real number, and we know from real analysis that positive real numbers have reciprocals. Thus \(\frac {1}{z\bar z}\in \R \). We can multiply complex numbers by real numbers, so \(\frac {1}{z\bar z}\bar z\) is a complex number and it is the \(w\) of the problem statement.
If \(z\) is a complex number, we define its modulus \(|z|\) as \(|z|=\sqrt {z\bar z}\).
\(|\re z|\leq |z|\) and \(|\im z|\leq |z|\) (where the first \(|\,\cdot \,|\) denotes the absolute value in the real numbers and the second \(|\,\cdot \,|\) denotes the modulus in the complex numbers.)
If \(z\) and \(w\) are complex numbers, show that \(|zw|=|z|\,|w|\).
Give an example of a non-constant polynomial that has no roots (solutions) that are real numbers. Find a root (solution) to your polynomial that is a complex number.
If \(z=x+iy=(x,y)\), then the complex modulus \(|z|\) is equal to the vector space norm \(\|(x,y)\|\) in \(\R ^2\).
\(\C \) is complete as a metric space if we use the expected metric \(d(z,w)=|z-w|\).
Recall that \((\R ^2,d)\) is a metric space, where \(d(u,v)=\|u-v\|\). In particular, this metric satisfies the triangle inequality. Write the triangle inequality as a statement about moduli of complex numbers. Simplify your statement as much as possible.
The conclusion is that \(|z+w|\leq |z|+|w|\) for all \(z\), \(w\in \C \). This is Proposition 1.2.3 in your textbook.
If \(\{a_n\}_{n=1}^\infty \) is a sequence of points in \(\R ^p\), \(a\in \R ^p\), and we write \(a_n=(a_n^1,a_n^2,\dots ,a_n^p)\), \(a=(a^1,\dots a^p)\), then \(a_n\to a\) (in the metric space sense) if and only if \(a_n^k\to a^k\) for each \(1\leq k\leq p\).
What does this tell you about the complex numbers?
If \(\{z_n\}_{n=1}^\infty \) is a sequence of points in \(\C \) and \(z\in \C \), then \(z_n\to z\) if and only if both \(\re z_n\to \re z\) and \(\im z_n\to \im z\).
If \(f:\R \to \R \) is an infinitely differentiable function, then the Maclaurin series for \(f\) is the power series
with the convention that \(0^0=1\).
If \(x\) is real, then the Maclaurin series for \(\exp x\), \(\sin x\), or \(\cos x\) converges to \(\exp x\), \(\sin x\), or \(\cos x\), respectively.
The Maclaurin series for the \(\exp \) function is \(\sum _{k=0}^\infty \frac {x^k}{k!}\).
The Maclaurin series for the \(\sin \) function is \(\sum _{k=0}^\infty (-1)^{k}\frac {x^{2k+1}}{(2k+1)!}\).
The Maclaurin series for the \(\cos \) function is \(\sum _{k=0}^\infty (-1)^{k}\frac {x^{2k}}{(2k)!}\).
If \(x\) and \(t\) are real numbers then
The Cauchy-Schwarz inequality for real numbers states that if \(n\in \N \) is a positive integer, and if for each \(k\) with \(1\leq k\leq n\) the numbers \(x_k\), \(\xi _k\) are real, then
State the Cauchy-Schwarz inequality for complex numbers and prove that it is valid.
This is Proposition 1.2.4 in your book. If \(n\in \N \), and if \(z_1\), \(z_2,\dots ,z_n\) and \(w_1\), \(w_2,\dots ,w_n\) are complex numbers, then\begin{equation*}\Bigl |\sum _{k=1}^n z_k\,w_k\Bigr |^2\leq \sum _{k=1}^n |z_k|^2 \sum _k |w_k|^2.\end{equation*}We can prove this as follows. By the triangle inequality, \(|z_1w_1+z_2w_2|\leq |z_1w_1|+|z_2w_2|=|z_1||w_1|+|z_2||w_2|\). A straightforward induction argument yields that
\begin{equation*}\Bigl |\sum _{k=1}^n z_k\,w_k\Bigr | \leq \sum _{k=1}^n|z_k||w_k|.\end{equation*}Applying the real Cauchy-Schwarz inequality with \(x_k=|z_k|\) and \(\xi _k=|w_k|\) completes the proof.
Let \(z\in \C \). Consider the series \(\sum _{k=0}^\infty \frac {z^k}{k!}\), that is, the sequence of complex numbers \(\bigl \{\sum _{k=0}^n \frac {z^k}{k!}\bigr \}_{n=0}^\infty \). Show that this sequence is a Cauchy sequence.
Since \(\C \) is complete, the series converges. If \(z=x\) is a real number, to what number does the series converge?
It converges to \(e^x\).
If \(z=iy\) is purely imaginary (that is, if \(y\in \R \)), show that \(\sum _{k=0}^\infty \frac {(iy)^k}{k!}\) converges to \(\cos y+i\sin y\).
An induction argument establishes that\begin{align*}\re i^k &= \begin {cases} 0, &k\text { is odd},\\1,&k\text { is even and a multiple of~$4$},\\-1,&k\text { is even and not a multiple of~$4$},\end {cases} \end{align*}and
\begin{align*} \im i^k &= \begin {cases} 0, &k\text { is even},\\1,&k\text { is odd and one more than a multiple of~$4$},\\-1,&k\text { is even and one less than a multiple of~$4$}.\end {cases} \end{align*}We then see that we may write the Maclaurin series for \(\cos \) and \(\sin \) as
\begin{equation*}\cos (y)=\sum _{k=0}^\infty \re i^k \frac {y^k}{k!}, \qquad \sin (y)=\sum _{k=0}^\infty \im i^k \frac {y^k}{k!} .\end{equation*}We then have that
\begin{equation*}\re \Bigl (\sum _{k=0}^n \frac {(iy)^k}{k!}\Bigr ) =\sum _{k=0}^n \re \biggl (\frac {(iy)^k}{k!}\biggr ) =\sum _{k=0}^n \re i^k\frac {y^k}{k!}\end{equation*}which converges to \(\cos y\) as \(n\to \infty \). Similarly
\begin{equation*}\im \Bigl (\sum _{k=0}^n \frac {(iy)^k}{k!}\Bigr ) =\sum _{k=0}^n \im \biggl (\frac {(iy)^k}{k!}\biggr ) =\sum _{k=0}^n \im i^k\frac {y^k}{k!}\end{equation*}converges to \(\sin y\) as \(n\to \infty \). Thus the series \(\sum _{k=0}^\infty \frac {(iy)^k}{k!}\) converges to \(\cos y+i\sin y\), as desired.
If \(z=x+iy\), show that \(\sum _{j=0}^\infty \frac {z^j}{j!}\) converges to the product \(\bigl (\sum _{j=0}^\infty \frac {x^j}{j!}\bigr )\bigl (\sum _{j=0}^\infty \frac {(iy)^j}{j!}\bigr )\).
If \(x\) is real, we define
If \(z=x+iy\) is a complex number, we define
If \(y\), \(\eta \) are real, show that \(\exp (iy+i\eta )=\exp (iy)\cdot \exp (i\eta )\).
Using the sum angle identities for sine and cosine, we compute\begin{align*} \exp (iy+i\eta ) &=\exp (i(y+\eta )) = \cos (y+\eta )+i\sin (y+\eta ) \\&= \cos y\cos \eta - \sin y\sin \eta + i\sin y\cos \eta +i \cos y\sin \eta \end{align*}and
\begin{align*} \exp (iy)\exp (i\eta )&= (\cos y+i\sin y)(\cos \eta +i\sin \eta ) \\&= \cos y\cos \eta - \sin y\sin \eta + i\sin y\cos \eta +i \cos y\sin \eta \end{align*}and observe that they are equal.
If \(z\), \(w\) are any complex numbers, show that \(\exp (z+w)=\exp (z)\cdot \exp (w)\).
There are real numbers \(x\), \(y\), \(\xi \), \(\eta \) such that \(z=x+iy\) and \(w=\xi +i\eta \).By definition
\begin{equation*}\exp (z)=\exp (x)\exp (iy),\qquad \exp (w)=\exp (\xi )\exp (i\eta ).\end{equation*}Because multiplication in the complex numbers is associative and commutative,
\begin{align*}\exp (z)\exp (w) &=[\exp (x)\exp (iy)][\exp (\xi )\exp (i\eta )] =[\exp (x)\exp (\xi )][\exp (iy)\exp (i\eta )] .\end{align*}By properties of exponentials in the real numbers and by the previous problem, we see that
\begin{align*} \exp (z)\exp (w) &=\exp (x+\xi )\exp (iy+i\eta ) .\end{align*}By definition of the complex exponential,
\begin{align*}\exp (z)\exp (w)&=\exp ((x+\xi )+i(y+\eta ))=\exp (z+w)\end{align*}as desired.
Suppose that \(z\) is a complex number and that \(|z|=1\). Show that there is a number \(\theta \in \R \) with \(\exp (i\theta )=z\). How many such numbers \(\theta \) exist? (Use only undergraduate real analysis and methods established so far in this course.)
We know from real analysis that, if \((x,y)\) lies on the unit circle, then \((x,y)=(\cos \theta ,\sin \theta )\) for some real number \(\theta \). By definition of complex modulus, if \(|z|=1\) and \(z=x+iy\) then \((x,y)\) lies on the unit circle. Thus \(z=\cos \theta +i\sin \theta =\exp (i\theta )\) for some \(\theta \in \R \).Infinitely many such numbers \(\theta \) exist.
If \(\theta \), \(\varpi \in \R \), then \(e^{i\theta }=e^{i\varpi }\) if and only if \((\theta -\varpi )/(2\pi )\) is an integer.
Suppose that \(z\) is a complex number. Show that there exist numbers \(r\in [0,\infty )\) and \(\theta \in \R \) such that \(z=r\exp (i\theta )\). How many possible values of \(r\) exist? How many possible values of \(\theta \) exist? (Use only undergraduate real analysis and methods established so far in this course.)
Observe that \(|re^{i\theta }|=r|e^{i\theta }|\) because \(r\geq 0\) and because the modulus distributes over products. But \(|e^{i\theta }|=|\cos \theta +i\sin \theta |=\sqrt {\cos ^2\theta +\sin ^2\theta }=1\), and so the only choice for \(r\) is \(r=|z|\).If \(z=0\) then we must have that \(r=0\) and can take any real number for \(\theta \).
If \(z\neq 0\), let \(r=|z|\). Then \(w=\frac {1}{r}z\) is a complex number with \(|z|=1\), and so there exist infinitely many values \(\theta \) with \(e^{i\theta }=w\) and thus \(z=re^{i\theta }\).
Find all solutions to the equation \(z^6=i\). Use only undergraduate real analysis and methods established so far in this course.
Suppose that \(z=re^{i\theta }\) for some \(r\geq 0\), \(\theta \in \R \).Then \(z^6=r^6 e^{6i\theta }\). If \(z^6=i\), then \(1=|i|=|z^6|=r^6\) and so \(r=1\) because \(r\geq 0\). We must then have that \(i=e^{6i\theta }\). Observe that \(i=e^{i\pi /2}\). By Homework 1.25, we must have that \(6\theta =\pi /2+2\pi n\) for some \(n\in \Z \), and so \((e^{i\theta })^6=i\) if and only if \(\theta =\pi /12+n \pi /3\). Thus the solutions are
\begin{equation*}e^{\pi /12},\quad e^{5\pi /12},\quad e^{9\pi /12},\quad e^{13\pi /12},\quad e^{17\pi /12},\quad e^{21\pi /12}.\end{equation*}Any other solution is of the form \(e^{i\theta }\), where \(\theta \) differs from one of the listed numbers by \(2\pi \).
Give an example of a function that can be written in two different ways.
Let \(p:\R \to \R \) be a function. We say that \(p\) is a (real) polynomial in one (real) variable if there is a \(n\in \N _0\) and constants \(a_0\), \(a_1,\dots ,a_n\in \R \) such that \(p(x)=\sum _{k=0}^n a_k x^k\) for all \(x\in \R \).
Let \(p:\R ^2\to \R \) be a function. We say that \(p\) is a (real) polynomial in two (real) variables if there is a \(n\in \N _0\) and constants \(a_{k,\ell }\in \R \) such that \(p(x,y)=\sum _{k=0}^n \sum _{\ell =0}^n a_{k,\ell } x^k y^\ell \) for all \(x\), \(y\in \R \).
Let \(p(x)=\sum _{k=0}^n a_k\,x^k\) and let \(q(x)=\sum _{k=0}^n b_k\,x^k\) be two polynomials in one variable, with \(a_k\), \(b_k\in \R \). Show that if \(p(x)=q(x)\) for all \(x\in \R \) then \(a_k=b_k\) for all \(k\in \N _0\).
\(p\) and \(q\) are infinitely differentiable functions from \(\R \) to \(\R \), and because \(p(x)=q(x)\) for all \(x\in \R \), we must have that \(p'=q'\), \(p''=q'',\dots ,p^{(k)}=q^{(k)}\) for all \(k\in \N \).We compute \(p^{(k)}(0)=k!a_k\) and \(q^{(k)}(0)=k!b_k\). Setting them equal we see that \(a_k=b_k\).
If \(p(z)=\sum _{k=0}^n a_k\,z^k\), then the degree of \(p\) is the largest nonnegative integer \(m\) such that \(a_m\neq 0\). (The degree of the zero polynomial \(p(z)=0\) is either undefined, \(-1\), or \(-\infty \).)
Let \(p\) be a polynomial. Suppose that \(x_0\in \R \) and that \(p(x_0)=0\). Show that there exists a polynomial \(q\) such that \(p(x)=(x-x_0)q(x)\) for all \(x\in \R \). Further show that, if \(p\) is a polynomial of degree \(m\geq 0\), then \(q\) is a polynomial of degree \(m-1\). Hint: Use induction.
If \(p\) is the zero polynomial we may take \(q\) to also be the zero polynomial. If \(p\) is a nonzero constant polynomial then no such \(x_0\) can exist. We therefore need only consider the case where \(p\) is a polynomial of degree \(m\geq 1\).If \(m=1\), then \(p(x)=a_1x+a_0\) for some \(a_1\), \(a_0\); if \(p(x_0)=0\) then \(a_0=-a_1x_0\) and so \(p(x)=a_1(x-x_0)\). Then \(q(x)=a_1\) is a polynomial of degree \(0=m-1\).
Suppose that the statement is true for all polynomials of degree at most \(m-1\), \(m\geq 2\). Let \(p\) be a polynomial of degree \(m\). Then \(p(x)=a_m x^m +r(x)\) where \(r\) is a polynomial of degree at most \(m-1\). We add and subtract \(a_m x_0 x^{m-1}\) to see that
\begin{equation*}p(x)=a_m x^{m-1} (x-x_0) + a_mx_0 x^{m-1}+r(x).\end{equation*}Then \(s(x)=a_mx_0 x^{m-1}+r(x)\) is a polynomial of degree at most \(m-1\). If \(s\) is a constant then \(0=p(x_0)=a_m x_0^{m-1}(x-x_0)+s\) and so \(s=0\); taking \(q(x)=a_mx^{m-1}\) we are done.
Otherwise, \(s(x)\) is a polynomial of degree at least one and at most \(m-1\). Also, \(s(x_0)=p(x_0)-a_mx_0^m(x_0-x_0)=0\), so by the induction hypothesis \(s(x)=(x-x_0)t(x)\) for a polynomial \(t\) of degree at most \(m-2\). Taking \(q(x)=a_mx^{m-1}+t(x)\) we are done.
Let \(p(x)=\sum _{k=0}^n a_k\,x^k\) and let \(q(x)=\sum _{k=0}^n b_k\,x^k\) be two polynomials of degree at most \(n\), with \(a_k\), \(b_k\in \R \) and \(n\in \N _0\). Suppose that there are \(n+1\) distinct numbers \(x_0,x_1,\dots ,x_n\in \R \) such that \(p(x_j)=q(x_j)\) for all \(0\leq j\leq n\). Show that \(a_k=b_k\) for all \(k\in \N _0\). Hint: Consider the polynomial \(r(x)=p(x)-q(x)\).
Let \(r(x)=p(x)-q(x)\). Then \(r(x_j)=p(x_j)-q(x_j)=0\) for all \(0\leq j\leq n\) and \(r\) is a polynomial of degree at most \(n\). Furthermore, \(r(x_j)=0\) for all \(0\leq j\leq n\).
Suppose for the sake of contradiction that \(r\) is not identically equal to zero. Then \(r\) is a polynomial of degree \(m\), \(0\leq m\leq n\). By 410Problem 410,
\begin{equation*}r(x)=(x-x_1)(x-x_2)\dots (x-x_m)r_m(x)\end{equation*}where \(r_m\) is a polynomial of degree \(m-m\), that is, a constant. But
\begin{equation*}0=p(x_0)-q(x_0)=r(x_0)=(x_0-x_1)(x_0-x_2)\dots (x_0-x_m) r_m(x_0).\end{equation*}Since \(x_j\neq x_0\) for all \(j\geq 1\) we must have that \(r_m(x_0)=0\); thus \(r_m\) is the constant function zero and so \(r\) is the constant function zero, as was to be proven. (This is technically a contradiction to the assumption \(m\geq 0\) because if \(m\geq 0\) then \(r\) is not the zero polynomial.)
Let \(p(x,y)=\sum _{j=0}^n\sum _{k=0}^n a_{j,k}\,x^j\,y^k\) and let \(q(x,y)=\sum _{j=0}^n\sum _{k=0}^n b_{j,k}\,x^j\,y^k\) be two polynomials of two variables, with \(a_{j,k}\), \(b_{j,k}\in \R \). Show that if \(p(x,y)=q(x,y)\) for all \((x,y)\in \R ^2\) then \(a_{j,k}=b_{j,k}\) for all \(j\), \(k\in \N _0\).
Fix a \(y\in \R \). Then \(p_y(x)=\sum _{j=0}^n \Bigl (\sum _{k=0}^n a_{j,k}y^k\Bigr ) x^j\) and \(q_y(x)=\sum _{j=0}^n \Bigl (\sum _{k=0}^n b_{j,k}y^k\Bigr ) x^j\) are both polynomials in one variable that are equal for all \(x\). So by 400Problem 400 their coefficients must be equal, so \(\Bigl (\sum _{k=0}^n a_{j,k}y^k\Bigr )=\Bigl (\sum _{k=0}^n b_{j,k}y^k\Bigr )\). This is true for all \(y\in \R \); another application of 400Problem 400 shows that \(a_{j,k}=b_{j,k}\) for all \(j\) and \(k\).
Give an example of a polynomial of two variables \(p\) such that \(p(x,y)=0\) for infinitely many values of \((x,y)\), but such that \(p\) is not the zero polynomial.
The polynomial \(p(x,y)=xy\) is such a polynomial, because \(p(0,y)=0\) and \(p(x,0)=0\) for all \(x\in \R \) or \(y\in \R \), and there are infinitely many \(x\in \R \) and infinitely many \(y\in \R \).
If \(\Omega \subseteq \R ^2\) is both open and connected, then \(\Omega \) is path connected: for every \(z\), \(w\in \Omega \) there is a continuous function \(\gamma :[0,1]\to \Omega \) such that \(\gamma (0)=z\) and \(\gamma (1)=w\).
If \(\Omega \subseteq \R ^2\) is open and connected, we may require the paths in the definition of path connectedness to be \(C^1\).
If \(\Omega \subseteq \R ^2\) is open and connected, we may require the paths in the definition of path connectedness to consist of finitely many horizontal or vertical line segments.
Let \(\Omega \subseteq \R ^2\) be open. Suppose that \(f:\Omega \to \R \). We say that \(f\) is continuously differentiable, or \(f\in C^1(\Omega )\), if the two partial derivatives \(\frac {\partial f}{\partial x}\) and \(\frac {\partial f}{\partial y}\) exist everywhere in \(\Omega \) and \(f\), \(\frac {\partial f}{\partial x}\), and \(\frac {\partial f}{\partial y}\) are all continuous on \(\Omega \).
Let \(B=B(z,r)\) be a ball in \(\R ^2\). Let \(f\in C^1(B)\) and suppose that \(\frac {\partial f}{\partial y}=\frac {\partial f}{\partial x}=0\) everywhere in \(B\). Show that \(f\) is a constant.
Let \(z=(x,y)\). Let \((\xi ,\eta )\in B((x,y),r)\).We consider the case \(\xi \geq x\) and \(\eta \geq y\); the cases \(\xi <x\) or \(\eta <y\) are similar. Then \(\{(t,y):x\leq t\leq \xi \}\subset B((x,y),r)\), and if we let \(F_y(x)=F(x,y)\), then \(F_y\) is a continuously differentiable function on \([x,\xi ]\) with \(F_y'(t)=0\) for all \(x\leq t\leq \xi \); by the Mean Value Theorem, \(F_y(x)=F_y(\xi )\) and so \(f(x,y)=f(\xi ,y)\). Similarly, \(\{(\xi ,t):y\leq t\leq \eta \}\subset B((x,y),r)\), and so \(f(x,y)=f(\xi ,y)=f(\xi ,\eta )\).
Thus \(f\) is a constant in \(B((x,y),r)\).
Suppose that \(\Omega \subseteq \R ^2\) is open and connected. Let \(f\in C^1(\Omega )\) and suppose that \(\frac {\partial f}{\partial y}=\frac {\partial f}{\partial x}=0\) everywhere in \(\Omega \). Show that \(f\) is a constant.
Let \(p:\C \to \C \) be a function. We say that \(p\) is a polynomial in one (complex) variable if there is a \(n\in \N _0\) and constants \(a_0\), \(a_1,\dots ,a_n\in \C \) such that \(p(z)=\sum _{k=0}^n a_k z^k\) for all \(z\in \C \).
Let \(p:\C \to \C \) be a function. We say that \(p\) is a polynomial in two real variables if there is a \(n\in \N _0\) and constants \(a_{k,\ell }\in \C \) such that \(p(x+iy)=\sum _{k=0}^n \sum _{\ell =0}^n a_{k,\ell } x^k y^\ell \) for all \(x\), \(y\in \R \).
430Problem 430 is true for complex polynomials of two real variables; that is, if \(p(x+iy)=\sum _{k,\ell =0}^n a_{k,\ell } x^ky^\ell \), \(q(x+iy)=\sum _{k,\ell =0}^n c_{k,\ell } x^ky^\ell \), and \(p(z)=q(z)\) for all \(z\in \C \), then \(a_{k,\ell }=c_{k,\ell }\) for all \(k\) and \(\ell \).
400Problem 400, 410Problem 410, and 420Problem 420 are valid for complex polynomials of one complex variable. There are complex polynomials of two real variables with infinitely many zeroes, as in 431Problem 431, that are not the zero polynomial.
The functions \(p(x+iy)=x\) and \(q(x+iy)=x^2\) are both clearly polynomials of two real variables. Prove that neither is a polynomial of one complex variable.
Show that \(p\) is a polynomial in two real variables if and only if there are constants \(b_{k,\ell }\in \C \) such that \(p(z)=\sum _{k=0}^n \sum _{\ell =0}^n b_{k,\ell } z^k \bar z^\ell \) for all \(z\in \C \).
430Problem 430 is true for complex polynomials of two real variables written in this form; that is, if \(p(z)=\sum _{k,\ell =0}^n b_{k,\ell } z^k\bar z^\ell \), \(q(z)=\sum _{k,\ell =0}^n d_{k,\ell } z^k\bar z^\ell \), and \(p(z)=q(z)\) for all \(z\in \C \), then \(b_{k,\ell }=d_{k,\ell }\) for all \(k\) and \(\ell \).
Let \(\Omega \subseteq \C \) be an open set. Recall \(\C =\R ^2\). Let \(f:\Omega \to \C \) be a function. Then \(f\in C^1(\Omega )\) if \(\re f\), \(\im f\in C^1(\Omega )\).
Let \(f\in C^1(\Omega )\). Let \(u(z)=\re f(z)\) and let \(v(z)=\im f(z)\). Then
Let \(\Psi \), \(\Omega \subseteq \C \) be two open sets, and let \(f:\Psi \to \Omega \) and \(g:\Omega \to \C \) be two \(C^1\) functions. What is \(\p {x}(g\circ f)\)?
Establish the Leibniz rules
for \(f\), \(g\in C^1(\Omega )\).
Let \(f=u+iv\), \(g=w+i\varpi \), where \(u\), \(v\), \(w\), and \(\varpi \) are real-valued functions in \(C^1(\Omega )\).Then \(fg=(uw-v\varpi )+i(vw+u\varpi )\), where \((uw-v\varpi )\) and \((vw+u\varpi )\) are both real-valued \(C^1\) functions.
Then
\begin{align*} \frac {\partial }{\partial x} (fg) &=\frac {\partial }{\partial x} [(uw-v\varpi )+i(vw+u\varpi )] \\&= \frac {\partial }{\partial x}(uw-v\varpi )+i\frac {\partial }{\partial x}(vw+u\varpi ). \end{align*}Applying the Leibniz (product) rule for real-valued functions, we see that
\begin{align*} \frac {\partial }{\partial x} (fg) &=\frac {\partial u}{\partial x}w + u\frac {\partial w}{\partial x}-\frac {\partial v}{\partial x}\varpi -v\frac {\partial \varpi }{\partial x} \\&\qquad + i\frac {\partial v}{\partial x}w + iv\frac {\partial w}{\partial x}+i\frac {\partial u}{\partial x}\varpi +iu\frac {\partial \varpi }{\partial x}. \end{align*}Furthermore,
\begin{align*} f\frac {\partial g}{\partial x}+\frac {\partial f}{\partial x} g &= (u+iv) \biggl (\frac {\partial w}{\partial x}+i\frac {\partial \varpi }{\partial x}\biggr ) \\&\qquad +\biggl (\frac {\partial u}{\partial x}+i\frac {\partial v}{\partial x}\biggr )(w+i\varpi ) \\&= u\frac {\partial w}{\partial x}+iu\frac {\partial \varpi }{\partial x}+iv\frac {\partial w}{\partial x}-v\frac {\partial \varpi }{\partial x}\\&\qquad +\frac {\partial u}{\partial x}w+i\frac {\partial u}{\partial x}\varpi +i\frac {\partial v}{\partial x}w -\frac {\partial v}{\partial x}\varpi . \end{align*}Rearranging, we see that the two terms are the same.
Let \(f\in C^1(\Omega )\). Then
Let \(f(z)=z\) and let \(g(z)=\bar z\). Show that \(\frac {\partial f}{\partial z}=1\), \(\frac {\partial f}{\partial \bar z}=0\), \(\frac {\partial g}{\partial z}=0\), \(\frac {\partial g}{\partial \bar z}=1\).
Recall that \(z=x+iy\). Thus,\begin{equation*}\frac {\partial }{\partial z} (z) = \frac {1}{2}\frac {\partial }{\partial x}(x+iy)+\frac {1}{2i}\frac {\partial }{\partial y}(x+iy) =\frac {1}{2}+\frac {i}{2i}=1 \end{equation*}and
\begin{equation*}\frac {\partial }{\partial \bar z} (z) = \frac {1}{2}\frac {\partial }{\partial x}(x+iy)-\frac {1}{2i}\frac {\partial }{\partial y}(x+iy) =\frac {1}{2}-\frac {i}{2i}=0 .\end{equation*}Recall that \(\bar z=x-iy\). Thus,
\begin{equation*}\frac {\partial }{\partial z} (\bar z) = \frac {1}{2}\frac {\partial }{\partial x}(x-iy)+\frac {1}{2i}\frac {\partial }{\partial y}(x-iy) =\frac {1}{2}-\frac {i}{2i}=0 \end{equation*}and
\begin{equation*}\frac {\partial }{\partial \bar z} (\bar z) = \frac {1}{2}\frac {\partial }{\partial x}(x-iy)-\frac {1}{2i}\frac {\partial }{\partial y}(x-iy) =\frac {1}{2}+\frac {i}{2i}=1 .\end{equation*}
\(\frac {\partial }{\partial z}\) and \(\frac {\partial }{\partial \bar z}\) are linear operators.
This follows immediately from linearity of the differential operators \(\frac {\partial }{\partial x}\) and \(\frac {\partial }{\partial y}\).
\(\frac {\partial }{\partial z}\) and \(\frac {\partial }{\partial \bar z}\) commute in the sense that, if \(\Omega \subseteq \C \) is open and \(f\in C^2(\Omega )\), then \(\frac {\partial }{\partial z}\left (\frac {\partial }{\partial \bar z} f\right )=\frac {\partial }{\partial \bar z}\left (\frac {\partial }{\partial z} f\right )\).
The following Leibniz rules are valid:
We have that\begin{align*} \frac {\partial }{\partial z} (fg) =\frac {1}{2}\frac {\partial }{\partial x} (fg) +\frac {1}{2i}\frac {\partial }{\partial y} (fg) .\end{align*}Using the Leibniz rules for \(\frac {\partial }{\partial x}\) and \(\frac {\partial }{\partial y}\), we see that
\begin{align*} \frac {\partial }{\partial z} (fg) &=\frac {1}{2}f\frac {\partial g}{\partial x} +\frac {1}{2}\frac {\partial f}{\partial x} g +\frac {1}{2i}f\frac {\partial g}{\partial y}+\frac {1}{2i}\frac {\partial f}{\partial y}g \\&= f\biggl (\frac 12\frac {\partial g}{\partial x}+\frac {1}{2i}\frac {\partial g}{\partial y}\biggr ) +\biggl (\frac {1}{2}\frac {\partial f}{\partial x}+\frac {1}{2i}\frac {\partial f}{\partial y}\biggr )g \\&=f\frac {\partial g}{\partial z}+\frac {\partial f}{\partial z}g .\end{align*}The argument for \(\frac {\partial }{\partial \bar z}\) is similar.
Show that \(\frac {\partial }{\partial z} (z^\ell \bar z^m)=\ell z^{\ell -1}\bar z^m\) and \(\frac {\partial }{\partial \bar z} (z^\ell \bar z^m)=mz^\ell \bar z^{m-1}\) for all nonnegative integers \(m\) and \(\ell \) (with the minor abuse of notation that we take \(z^0\equiv \bar z^0\equiv 1\) and \(0z^{-1}\equiv 0\bar z^{-1}\equiv 0\), that is, we ignore the singularities at \(z=0\)).
If \(\ell =m=0\), then \(z^\ell \bar z^m=1\) and \(\ell z^{\ell -1}\bar z^m=0=mz^\ell \bar z^{m-1}\). The result is obvious in this case.Suppose now that \(m=0\), \(\ell \geq 1\) and the result is true for \(\ell -1\). (The result is true for \(\ell -1\) if \(\ell =1\) by the above argument.) By 570Fact 570,
\begin{align*} \p { z} z^\ell &=\p { z}(z\cdot z^{\ell -1}) = \biggl (\p { z}z\biggr )z^{\ell -1}+z\biggl (\p { z}z^{\ell -1}\biggr ), \\ \p {\bar z} z^\ell &=\p {\bar z}(z\cdot z^{\ell -1}) = \biggl (\p {\bar z}z\biggr )z^{\ell -1}+z\biggl (\p {\bar z}z^{\ell -1}\biggr ), \end{align*}which by the induction hypothesis and 540Problem 540 equal
\begin{align*} \p { z} z^\ell = z^{\ell -1}+z\cdot (\ell -1)z^{\ell -2}, \\ \p {\bar z} z^\ell = 0\cdot z^{\ell -1}+z\cdot 0, \end{align*}which simplify to the desired result. Thus by induction the result is true whenever \(m=0\). A similar induction argument yields the result whenever \(\ell =0\). Finally, the general case follows from 570Fact 570 as follows:
\begin{align*} \frac {\partial }{\partial z} (z^\ell \bar z^m)&= \biggl (\p {z}z^\ell \biggr )\bar z^m+z^\ell \biggl (\p { z}\bar z^m\biggr ) = \ell z^{\ell -1}\bar z^m+0,\\ \frac {\partial }{\partial \bar z} (z^\ell \bar z^m)&= \biggl (\p {\bar z}z^\ell \biggr )\bar z^m+z^\ell \biggl (\p {\bar z}\bar z^m\biggr ) = 0+ z^{\ell }\cdot m\bar z^{m-1} \end{align*}as desired.
Let \(p\) be a complex polynomial in two real variables. Show that \(p\) is a complex polynomial in one complex variable if and only if \(\frac {\partial p}{\partial \bar z}=0\) everywhere in \(\C \).
If \(p\) is a polynomial in one complex variable, then by definition there are constants \(a_k\in \C \) and \(n\in \N \) such that \(p(z)=\sum _{k=0}^n a_k z^k\). By linearity of the complex derivative operator and by 580Problem 580, we have that \(\p {\bar z} p(z)=0\), as desired.Now suppose that \(p\) is a complex polynomial in two real variables and \(\p {\bar z} p(z)=0\) for all \(z\in \C \). By 510Problem 510, there are constants \(b_{k,\ell }\in \C \) and \(m\in \N \) such that
\begin{equation*}p(z)=\sum _{k=0}^m \sum _{\ell =0}^m b_{k,\ell } z^k\bar z^\ell \end{equation*}for all \(z\in \C \). By linearity of the complex derivative operator and by 580Problem 580, we have that
\begin{equation*}\p {\bar z} p(z)=\sum _{k=0}^m \sum _{\ell =0}^m \ell b_{k,\ell } z^k\bar z^{\ell -1}.\end{equation*}This polynomial is identically equal to zero. By 511Problem 511, this implies that \(\ell b_{k,\ell }=0\) for all \(k\) and \(\ell \). In particular, if \(\ell \geq 1\) then \(b_{k,\ell }=0\). Thus
\begin{equation*}p(z)=\sum _{k=0}^m b_{k,0} z^k\end{equation*}as desired.
Let \(\Omega \subseteq \C \) be open and let \(f\in C^1(\Omega )\). We say that \(f\) is holomorphic in \(\Omega \) if
everywhere in \(\Omega \).
A polynomial in two real variables is a polynomial in one complex variable if and only if it is holomorphic.
Suppose that \(\Omega \subseteq \C \) is open and connected, that \(f\in C^1(\Omega )\), and that \(\frac {\partial f}{\partial z}=0=\frac {\partial f}{\partial \bar z}\) in \(\Omega \). Show that \(f\) is constant in \(\Omega \).
We observe that\begin{equation*}\p [f]{x}=\p [f]{z}+\p [f]{{\bar z}},\qquad \p [f]{y}=i\p [f]{z}-i\p [f]{{\bar z}}.\end{equation*}Thus \(\p [f]{x}=\p [f]{y}=0\) in \(\Omega \) and the result follows from 480Problem 480.
Suppose that \(\Omega \subseteq \C \) is open and that \(f\in C^1(\Omega )\). Show that
for all \(w\in \Omega \).
Show that \(\frac {\partial }{\partial z}\frac {1}{z}=-\frac {1}{z^2}\) and \(\frac {\partial }{\partial \bar z}\frac {1}{z}=0\) if \(z\neq 0\). Then compute \(\frac {\partial }{\partial z}\frac {1}{z^n}\) and \(\frac {\partial }{\partial \bar z}\frac {1}{z^n}\) for any positive integer \(n\).
Observe that \(\frac {1}{z}=\frac {\bar z}{z\bar z}\) and so if \(z=x+iy\), \(x\), \(y\in \R \), then \(\frac {1}{z}=\frac {x-iy}{x^2+y^2}\). We compute\begin{align*}\p {x}\frac {1}{z}&= \p {x}\re \frac {1}{z} +i\p {x}\im \frac {1}{z}= \p {x}\frac {x}{x^2+y^2} +i\p {x}\frac {-y}{x^2+y^2} = \frac {y^2-x^2+2ixy}{(x^2+y^2)^2}, \\ \p {y}\frac {1}{z}&= \p {y}\frac {x}{x^2+y^2} +i\p {y}\frac {-y}{x^2+y^2} = \frac {-ix^2+iy^2-2xy}{(x^2+y^2)^2}. \end{align*}Thus
\begin{align*}\p {z}\frac {1}{z} &=\frac {1}{2} \p {x}\frac {1}{z}-\frac {i}{2}\p {y}\frac {1}{z} = \frac {y^2-x^2+2ixy}{(x^2+y^2)^2} \\&= \frac {-(x-iy)^2}{(x+iy)^2(x-iy)^2} =-\frac {1}{z^2} \end{align*}and
\begin{equation*}\p {z}\frac {1}{z} =\frac {1}{2} \p {x}\frac {1}{z}+\frac {i}{2}\p {y}\frac {1}{z} = 0. \end{equation*}Using the Leibniz rule for the inductive step, a straightforward induction argument shows that
\begin{equation*}\p {z}\frac {1}{z^n}=-\frac {n}{z^{n+1}}, \qquad \p {\bar z}\frac {1}{z^n} =0.\end{equation*}
Let \(\Omega \), \(W\subseteq \C \) be open and let \(g:\Omega \to W\), \(f:W\to \C \) be two \(C^1\) functions. The following chain rules are valid:
where \(\frac {\partial f}{\partial g} = \left .\frac {\partial f}{\partial z}\right |_{z\to g(z)}\), \(\frac {\partial f}{\partial \overline g} = \left .\frac {\partial f}{\partial \bar z}\right |_{z\to g(z)}\).
In particular, if \(f\) and \(g\) are both holomorphic then so is \(f\circ g\).
Let \(f\) be a \(C^2\) function in an open set in \(\R ^2\). Show that \(\frac {\partial }{\partial x} \frac {\partial f}{\partial y}=\frac {\partial }{\partial y} \frac {\partial f}{\partial x}\) everywhere in the domain.
Let \(f\in C^1(\Omega )\), let \(u=\re f\), and let \(v=\im f\). Then \(f\) is holomorphic in \(\Omega \) if and only if
everywhere in \(\Omega \). (These equations are called the Cauchy-Riemann equations.)
Prove the “only if” direction of Lemma 1.4.2: show that if \(f\) is holomorphic in \(\Omega \), \(\Omega \subseteq \C \) open, then the Cauchy-Riemann equations hold for \(u=\re f\) and \(v=\im f\).
Prove the “if” direction of Lemma 1.4.2: show that if \(u=\re f\) and \(v=\im f\) are \(C^1\) in \(\Omega \) and satisfy the Cauchy-Riemann equations, then \(f\) is holomorphic in \(\Omega \).
Recall that\begin{align*} 2\p [f]{\bar z} = \p [f]{x} +i\p [f]{y} \end{align*}by definition of \(\p {\bar z}\). Applying the fact that \(f=u+iv\), we see that
\begin{align*} 2\p [f]{\bar z}&=\p [u]{x}+i\p [v]{x} +i \biggl (\p [u]{y}+i\p [v]{y}\biggr ) \\&= \biggl (\p [u]{x}-\p [v]y\biggr )+ i\biggl (\p [v]x+\p [u]y\biggr ). \end{align*}Because \(u\) and \(v\) are real-valued, so are their derivatives. Thus, the real and imaginary parts of the right hand side, respectively, are \(\p [u]x-\p [v]y\) and \(\p [u]y+\p [v]x\).
Thus, \(\p [f]{\bar z} = 0\) if and only if the Cauchy-Riemann equations hold.
Show that the function \(\exp \) is holomorphic.
Recall that \(\exp \) is given by \(\exp (x+iy)=e^x(\cos y+i\sin y)=e^x\cos y+ie^x\sin y\).Writing \(u(x,y)=e^x\cos y\), \(v(x,y)=e^x\sin y\), we have that
\begin{equation*}\frac {\partial u}{\partial x} = e^x\cos y=\frac {\partial v}{\partial y}, \quad \frac {\partial u}{\partial y} = -e^x\sin y=-\frac {\partial v}{\partial x},\end{equation*}and so \(u\) and \(v\) satisfy the Cauchy-Riemann equations; thus \(f(x,y)=u(x,y)+iv(x,y)=\exp (x+iy)\) is holomorphic.
[Slight generalization.] Let \(f\in C^1(\Omega )\). Then \(f\) is holomorphic at \(p\in \Omega \) if and only if \(\frac {\partial f}{\partial x}(p)=\frac {1}{i}\frac {\partial f}{\partial y}(p)\) and that in this case
Begin the proof of Proposition 1.4.3 by showing that if \(f\) is holomorphic then \(\frac {\partial f}{\partial z}=\frac {\partial f}{\partial x}=\frac {1}{i}\frac {\partial f}{\partial y}\).
By definition of \(\p {z}\) and \(\p {\bar z}\), if \(f\in C^1(\Omega )\) then \(\p [f]{x}=\p [f]{z}+\p [f]{\bar z}\) and \(\p [f]{y}=i\p [f]{z}-i\p [f]{\bar z}\). Thus, if \(\p [f]{\bar z}(p)=0\) then \(\p [f]{x}(p)=\p [f]{z}(p)\) and \(\p [f]{y}(p)=i\p [f]{z}(p)=i\p [f]{x}(p)\), as desired.
Complete the proof of Proposition 1.4.3 by showing that if \(f\in C^1(\Omega )\) and \(\frac {\partial f}{\partial x}=\frac {1}{i}\frac {\partial f}{\partial y}\), then \(f\) is holomorphic.
Recall\begin{equation*}\p [f]{\bar z} = \frac 12\biggl (\p [f]x- \frac {1}{i}\p [f]{y}\biggr ).\end{equation*}Thus, if \(\p [f]x=\frac {1}{i}\p [f]y\) then \(\p [f]{\bar z}=0\), as desired.
We let \(\triangle =\frac {\partial ^2 }{\partial x^2}+\frac {\partial ^2 }{\partial y^2}\). If \(\Omega \subseteq \C \) is open and \(u\in C^2(\Omega )\), then \(u\) is harmonic if
everywhere in \(\Omega \).
Show that if \(f\in C^1(\Omega )\) then \(\triangle f=4\frac {\partial }{\partial z}\frac {\partial f} {\partial \bar z} =4\frac {\partial }{\partial \bar z} \frac {\partial f}{\partial z}\).
We compute that\begin{align*}\p {z}\p [f]{\bar z} &= \frac {1}{4} \biggl (\p x+\frac {1}{i}\p y\biggr ) \biggl (\p [f] x-\frac {1}{i} \p [f] y\biggr ) \\&=\frac {1}{4}\biggl (\frac {\partial ^2f}{\partial x^2} +\frac {\partial ^2f}{\partial y^2} +\frac {1}{i}\frac {\partial ^2 f}{\partial y\,\partial x} -\frac {1}{i}\frac {\partial ^2 f}{\partial x\,\partial y}\biggr ) .\end{align*}If \(f\in C^1\) then \(\frac {\partial ^2 f}{\partial y\,\partial x} =\frac {\partial ^2 f}{\partial x\,\partial y}\) and the proof is complete. The argument for \(\p {\bar z}\p [f]{z} \) is similar.
Suppose that \(f\) is holomorphic and \(C^2\) in an open set \(\Omega \) and that \(u=\re f\) and \(v=\im f\). Compute \(\triangle u\) and \(\triangle v\).
Because \(f\) is holomorphic,\begin{equation*}\triangle f = 4\frac {\partial }{\partial z}\frac {\partial f} {\partial \bar z}=4\frac {\partial }{\partial z}0=0.\end{equation*}But
\begin{equation*}\triangle f = (\triangle u) + i(\triangle v)\end{equation*}and \(\triangle u\) and \(\triangle v\) are both real-valued, so because \(\triangle f=0\) we must have \(\triangle u=0=\triangle v\) as well.
Let \(f\) be a holomorphic polynomial. Show that there is a holomorphic polynomial \(F\) such that \(\frac {\partial F}{\partial z} = f\). How many such polynomials are there?
By 600Fact 600, \(f\) is a polynomial in one complex variable; that is, there is a \(n\in \N \) and constants \(a_k\in \C \) such that\begin{equation*}f(z)=\sum _{k=0}^n a_k\,z^k\end{equation*}for all \(z\in \C \). Let \(b\in \C \) and let
\begin{equation*}F(z)=b+\sum _{k=0}^n \frac {a_k}{k+1}\,z^{k+1}.\end{equation*}By 580Problem 580, we have that \(\p {z}F=f\).
There are infinitely many such polynomials, one for each choice of \(b\). By 610Problem 610, any two such antiderivatives \(F_1\) and \(F_2\) must differ by a constant.
Show that if \(u\) is a harmonic polynomial (of two real variables) then \(u(z)=p(z)+q(\bar z)\) for some polynomials \(p\), \(q\) of one complex variable.
Because \(u\) is harmonic, by 680Fact 680 we have that\begin{equation*}0=\triangle u=4\frac {\partial }{\partial \bar z} \frac {\partial u}{\partial z}\end{equation*}and so \(f=\p [u]{z}\) is holomorphic. By 580Problem 580 we have that \(f\) is a polynomial. Thus by 700Problem 700 there is a holomorphic polynomial \(F\) with \(\p [F]{z}=f=\p [u]{z}\).
Let \(p=F\). Let \(g(z)=u(z)-p(z)\). Then \(g\) is a polynomial and \(\p [g]{z}=0\), so by Problem 1.34 \(\p [\overline g]{\bar z}=0\). Thus
\begin{equation*}\overline {g(z)}=\sum _{k=0}^m b_k \,z^k\end{equation*}for some \(m\in \N \) and some constants \(b_k\in \C \). Taking the complex conjugate yields that
\begin{equation*}g(z)=\sum _{k=0}^m \overline {b_k}\,\bar z^k.\end{equation*}This completes the proof with \(q(z)=\sum _{k=0}^m \overline {b_k}\, z^k\).
Let \(u\) be harmonic and real valued in \(\C \). Suppose in addition that \(u\) is a polynomial of two real variables. Then there is a holomorphic polynomial \(f\) such that \(u(z)=\re f(z)\).
Prove Lemma 1.4.5.
By 710Problem 710, we have that \(u(z)=p(z)+q(\bar z)\) for some polynomials \(p\) and \(q\). We may write\begin{equation*}u(z)=\sum _{k=0}^n a_k z^k+\sum _{k=0}^n b_k \bar z^k =(a_0+b_0)+\sum _{k=1}^n a_k z^k+\sum _{k=1}^n b_k \bar z^k\end{equation*}for some \(n\in \N \) and some \(a_k\), \(b_k\in \C \). Because \(u\) is real-valued, we have that \(u(z)=\overline {u(z)}\) and so
\begin{equation*} (a_0+b_0)+\sum _{k=1}^n a_k z^k+\sum _{k=1}^n b_k \bar z^k = \overline {(a_0+b_0)}+\sum _{k=1}^n \overline {b_k} z^k+\sum _{k=1}^n \overline {a_k} \bar z^k. \end{equation*}By 511Problem 511, this implies that \(a_0+b_0\) is real and that \(a_k=\overline {b_k}\) for all \(k\geq 1\).
Thus
\begin{align*}u(z) &=(a_0+b_0)+ \sum _{k=1}^n (a_k z^k+\overline {a_k z^k}) =\re (a_0+b_0)+ \sum _{k=1}^n 2\re (a_k z^k) \\&=\re \Bigl ((a_0+b_0)+ \sum _{k=1}^n 2a_k z^k\Bigr )\end{align*}as desired.
State Green’s theorem.
Let \(\gamma :[0,1]\to \R ^2\) be a piecewise \(C^1\) simple closed curve.2 Let \(\Omega \subset \R ^2\) be the bounded open set that satisfies \(\partial \Omega =\gamma ([0,1])\); by the Jordan curve theorem, exactly one such \(\Omega \) exists. Let \(W\) be open and satisfy \(\overline \Omega \subset W\). Let \(\vec F:W\to \R ^2\) be a \(C^1\) function.Then
\begin{equation*}\int _0^1 \vec F(\gamma (t))\cdot \gamma '(t)\,dt = \pm \int _\Omega \frac {\partial F_2}{\partial x}-\frac {\partial F_1}{\partial y}\,dx\,dy\end{equation*}where the sign is determined by the orientation of \(\gamma \).
State the Mean Value Theorem.
If \(a<b\), if each \(f_n\) is bounded and Riemann integrable on \([a,b]\), and if \(f_n\to f\) uniformly on \([a,b]\), then \(f\) is also Riemann integrable on \([a,b]\), \(\lim _{n\to \infty } \int _a^b f_n\) exists, and \(\int _a^b f = \lim _{n\to \infty } \int _a^b f_n\).
Let \(f:[a,b]\times [c,d]\to \R \). Suppose that \(f\) is continuous on \([a,b]\times [c,d]\). Define \(F:[a,b]\to \R \) by \(F(x)=\int _{c}^d f(x,y)\,dy\). Show that \(F\) is continuous on \([a,b]\).
Let \(f:(a,b)\times [c,d]\to \R \). Suppose that \(f\) is continuous on \((a,b)\times [c,d]\) and the partial derivative \(\partial _xf=\frac {\partial f}{\partial x}\) exists and is continuous everywhere on \((a,b)\times [c,d]\). Define \(F(x)=\int _c^d f(x,y)\,dy\). Show that \(F\) is differentiable on \((a,b)\) and that
for all \(a<x<b\).
This will be proven as homework.
Prove the converse to Clairaut’s theorem. That is, suppose that there are two \(C^1\) functions \(g\) and \(h\) defined in an open rectangle or disc \(\Omega \) such that \(\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h\) everywhere in \(\Omega \). Show that there is a function \(f\in C^2(\Omega )\) such that \(\frac {\partial f}{\partial y}=g\) and \( \frac {\partial f}{\partial x}=h\).
State the definition of a simply connected set and then generalize 780Problem 780 to any simply connected open set.
Let \(\Omega =\R ^2\setminus \{(0,0)\}\). Let \(g(x,y)=\frac {x}{x^2+y^2}\) and \(h(x,y)=\frac {-y}{x^2+y^2}\). Show that \(\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h\).
This is routine calculation. By the quotient rule of undergraduate calculus,\begin{equation*}\p {x}g = \frac {1(x^2+y^2)-x(2x)}{(x^2+y^2)^2} = \frac {y^2-x^2}{(x^2+y^2)^2} \end{equation*}and
\begin{equation*}\p {y}h = \frac {-1(x^2+y^2)-(-y)(2y)}{(x^2+y^2)^2} = \frac {y^2-x^2}{(x^2+y^2)^2}\end{equation*}which are equal.
Show that there is no function \(f\in C^1(\Omega )\) such that \(\frac {\partial f}{\partial y}=g\) and \( \frac {\partial f}{\partial x}=h\).
Why doesn’t this contradict 790Bonus Problem 790?
The domain \(\Omega \) is not simply connected.
Suppose that \(u\) is real-valued and harmonic (and not necessarily a polynomial) in an open rectangle or disc \(\Omega \). Show that there is a function \(f\) that is holomorphic in \(\Omega \) such that \(u=\re f\).
Let \(g=\frac {\partial u}{\partial x}\) and let \(h=-\frac {\partial u}{\partial y}\). Then\begin{equation*}\p [g]{x}=\frac {\partial ^2 u}{\partial x^2} = -\frac {\partial ^2 u}{\partial y^2}=\p [h]{y}\end{equation*}by definition of \(g\) and \(h\) and because \(u\) is harmonic. Thus by 790Bonus Problem 790 there is a \(v:\Omega \to \R \) such that \(\p [v]{y}=g=\frac {\partial u}{\partial x}\) and \(\p [v]{x}=h=-\frac {\partial u}{\partial y}\).
Then \(u\) and \(v\) satisfy the Cauchy-Riemann equations, and so by 650Problem 650, \(f=u+iv\) is holomorphic in \(\Omega \).
Suppose that \(f\) is holomorphic in an open rectangle or disc \(\Omega \). Show that there is a function \(F\) that is holomorphic in \(\Omega \) such that \(f=\frac {\partial F}{\partial z}\). (We call \(F\) the holomorphic antiderivative of \(f\).)
The function \(f(z)=1/z\) is holomorphic on \(\Omega =\{z\in \C :1<|z|<2\}\) but has no holomorphic antiderivative on \(\Omega \).
Let \((a,b)\subset \R \) be an open interval, let \(\Omega \subseteq \R ^2\) be open, let \(\gamma :(a,b)\to \Omega \) be \(C^1\), and let \(f:\Omega \to \R \) be \(C^1\). Then
where \(\cdot \) is the dot product in the vector space \(\R ^2\), and \(\gamma _1\), \(\gamma _2:(a,b)\to \R \) are the \(C^1\) functions such that \(\gamma (t)=(\gamma _1(t),\gamma _2(t))\).
State the Intermediate Value Theorem.
State the change of variables theorem for integrals over real intervals.
Let \((X,d)\) and \((Z,\rho )\) be two metric spaces and let \(f:X\to Z\). We say that \(f\) is continuous at \(x\in X\) if, for all \(\varepsilon >0\), there is a \(\delta >0\) such that if \(d(x,y)<\delta \) and \(y\in X\) then \(\rho (f(x),f(y))<\varepsilon \).
Let \(a<b\) and let \(\varphi :[a,b]\to \R \) be continuous. Then \(\left |\int _a^b \varphi \right |\leq \int _a^b |\varphi |\leq (b-a)\sup _{[a,b]}|\varphi |\).
Let \(X\) be a compact metric space and let \(f:X\to Z\) be a continuous function. Then \(f\) is uniformly continuous.
Let \(X\) be a compact metric space and let \(f:X\to \R \) be a continuous function. Then \(f\) attains its maximum and minimum, that is, there are points \(m\) and \(M\) in \(X\) such that \(f(m)\leq f(x)\leq f(M)\) for all \(x\in X\). In particular, \(f\) is bounded on \(X\).
If \(\varphi :[c,d]\to [a,b]\) is a continuous bijection for \(a\), \(b\), \(c\), \(d\in \R \) with \(a<b\) and \(c<d\), show that either \(\varphi \) is strictly increasing, \(\varphi (c)=a\), and \(\varphi (d)=b\), or \(\varphi \) is strictly decreasing, \(\varphi (c)=b\), and \(\varphi (d)=a\).
Let \(m\), \(M\in [c,d]\) with \(\varphi (m)\leq \varphi (t)\leq \varphi (M)\) for all \(t\in [c,d]\). Such \(m\) and \(M\) exist by 872Memory 872.Suppose for the sake of contradiction that \(\varphi (m)<\varphi (c)\) and \(\varphi (m)<\varphi (d)\). Then \(c\neq m\neq d\) and so \(c<m<d\). Let \(y\) satisfy \(\varphi (m)<y<\min (\varphi (c),\varphi (d))\). By the intermediate value theorem, there are points \(t_1\) and \(t_2\) with \(c<t_1<m<t_2<d\) (in particular, \(t_1\neq t_2\)) and \(\varphi (t_1)=y=\varphi (t_2)\). But then \(\varphi \) is not injective. This contradicts our assumption on \(\varphi \), and so either \(\varphi (m)=\varphi (c)\) and so \(m=c\), or \(\varphi (m)=\varphi (d)\) and so \(m=d\).
Similarly, \(M\in \{c,d\}\). Since \(\varphi \) is injective, \(c<d\), and so \([c,d]\) contains more than one point, we have that \(M\neq m\) and so either \(M=c\), \(m=d\) or \(m=c\), \(M=d\).
If \(m=c\), \(M=d\), then \(\varphi (c)<\varphi (t)<\varphi (d)\) for all \(t\in (c,d)\). If \(c\leq t_1<t_2\leq d\) and \(\varphi (t_1)>\varphi (t_2)\), then another application of the intermediate value theorem contradicts injectivity of \(\varphi \), and so \(\varphi \) must be increasing; because \(\varphi \) is injective it must be strictly increasing. Similarly, if \(m=d\), \(M=c\), then \(\varphi \) is strictly decreasing, as desired.
Let \(X\) be a compact metric space and let \(f:X\to Z\) be a continuous function. Then \(f(X)\) is compact.
Let \(X\) be a compact metric space and let \(f:X\to Z\) be a continuous bijection. Then \(f^{-1}\) is also continuous.
Is the previous problem true if \(X\) is not compact?
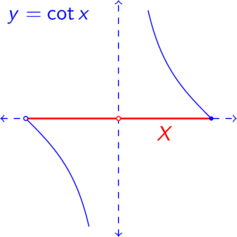
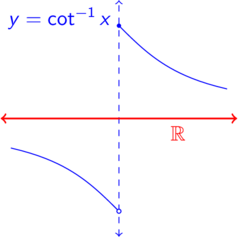
No. Let \(X=(-\pi /2,0)\cup (0,\pi /2]\subset \R \) with the usual metric on \(\R \). Then the function \(\cot :X\to \R \) is continuous on \(X\) and is a bijection, but \(\cot ^{-1}(0)=\frac {\pi }{2}\) and \(\lim _{x\to 0^-}\cot ^{-1}(x)=-\frac {\pi }{2}\), and so \(\cot ^{-1}\) (with the given range) is discontinuous at \(0\).
If \(\gamma :X\to \R ^2\) and \(\gamma (t)=(\gamma _1(t),\gamma _2(t))\) for all \(t\in X\), then \(\gamma \) is continuous if and only if \(\gamma _1\) and \(\gamma _2\) are continuous.
(\(C^1\) on a closed set.) Let \([a,b]\subseteq \R \) be a closed bounded interval and let \(f:[a,b]\to \R \). We say that \(f\in C^1([a,b])\), or \(f\) is continuously differentiable on \([a,b]\), if
If the conditions (a), (b) and (c) hold, then the condition (d) holds if and only if the two limits \(\lim _{t\to a^+} \frac {f(t)-f(a)}{t-a}\) and \(\lim _{t\to b^-} \frac {f(b)-f(t)}{b-t}\) exist, and in this case \(\lim _{t\to a^+} \frac {f(t)-f(a)}{t-a}=\lim _{t\to a^+} f'(t)\) and \(\lim _{t\to b^-} \frac {f(b)-f(t)}{b-t}=\lim _{t\to b^-} f'(t)\).
If \(f:[a,b]\to \R \), we define \(f'(a)=\lim _{t\to a^+} \frac {f(t)-f(a)}{t-a}\) and \(f'(b)=\lim _{t\to b^-} \frac {f(b)-f(t)}{b-t}\), if these limits exist.
A curve in \(\R ^2\) is a continuous function \(\gamma :[a,b]\to \C \), where \([a,b]\subseteq \R \) is a closed and bounded interval. The trace (or image) of \(\gamma \) is \(\widetilde \gamma =\gamma ([a,b])=\{\gamma (t):t\in [a,b]\}\).
A curve \(\gamma :[a,b]\to \R ^2\) is closed if \(\gamma (a)=\gamma (b)\). A closed curve is simple if \(\gamma (b)=\gamma (a)\) and \(\gamma \) is injective on \([a,b)\) (equivalently on \((a,b]\)).
A curve \(\gamma :[a,b]\to \R ^2\) is \(C^1\) (or continuously differentiable) if \(\gamma (t)=(\gamma _1(t),\gamma _2(t))\) for all \(t\in [a,b]\) and both \(\gamma _1\), \(\gamma _2\) are \(C^1\) on \([a,b]\). We write
If \(\gamma :[a,b]\to \R ^2\) is a \(C^1\) curve, then its length (or arc length) is \(\int _a^b \|\gamma '(t)\|\,dt\).
Let \(\gamma \in C^1([a,b])\), \(\gamma :[a,b]\to \Omega \) for some open set \(\Omega \subseteq \R ^2\) and let \(f:\Omega \to \R \) with \(f\in C^1(\Omega )\). Then
Prove Proposition 2.1.4. Hint: Start by computing \(\frac {d(f\circ \gamma )}{dt}\).
By the multivariable chain rule,\begin{equation*}\frac {d(f\circ \gamma )}{dt}= \frac {\partial f}{\partial x}\Big \vert _{(x,y)=\gamma (t)}\frac {\partial \gamma _1}{\partial t} +\frac {\partial f}{\partial y}\Big \vert _{(x,y)=\gamma (t)}\frac {\partial \gamma _2}{\partial t}.\end{equation*}The result then follows from the fundamental theorem of calculus.
Let \(\gamma \in C^1([a,b])\), \(\gamma :[a,b]\to \Omega \) for some open set \(\Omega \subseteq \R ^2\) and \(F:\Omega \to \R \) be continuous on \(\Omega \). We define
Let \(\vec F:\Omega \to \R ^2\) be continuous on \(\Omega \). We define
where we use a dot product in the second integral.
(Integral of a complex function.) If \(f:[a,b]\to \C \), and both \(\re f\) and \(\im f\) are integrable on \([a,b]\), we define \(\int _a^b f=\int _a^b\re f+i\int _a^b \im f\).
If \(\alpha \), \(\beta \in \C \) are constants and \(f\), \(g:[a,b]\to \C \) are both continuous, show that \(\int _a^b(\alpha f+\beta g)=\alpha \int _a^b f+\beta \int _a^b g\).
Suppose that \(a<b\) and that \(f:[a,b]\to \C \) is continuous. Then \(|\int _a^b f|\leq \int _a^b |f|\leq (b-a)\sup _{[a,b]}|f|\).
Prove Proposition 2.1.7. Hint: Start by showing that the integral is finite.
First,\begin{align*} \biggl |\int _a^b f\biggr | &\leq \biggl |\re \int _a^b f\biggr |+\biggl |\im \int _a^b f\biggr | = \biggl |\int _a^b \re f\biggr |+\biggl |\int _a^b \im f\biggr |. \end{align*}By continuity of \(\re f\) and \(\im f\) and compactness of \([a,b]\), we have that \(\sup _{[a,b]}|\re f|<\infty \) and \(\sup _{[a,b]}|\im f|<\infty \) and so the integral is finite by 870Memory 870.
If \(\int _a^b f=0\) we are done. Otherwise, let \(\theta \in \R \) be such that \(e^{i\theta }\int _a^b f\) is a nonnegative real number. Then \(|\int _a^b f|=\int e^{i\theta } f\). But \(|\int _a^b f|\) is real and so \(\im \int e^{i\theta } f=0\). Therefore \(|\int _a^b f|=\re \int e^{i\theta } f =\int \re (e^{i\theta } f)\). The result then follows from the corresponding result for real integrals.
(\(C^1\) curve in \(\C \).) A curve \(\gamma :[a,b]\to \C \) is a \(C^1\) curve (in \(\C \)) if \((\re \gamma ,\im \gamma )\) is a \(C^1\) curve (in \(\R ^2\)). We write
If \(t\in (a,b)\) and \(\gamma :[a,b]\to \C \) is \(C^1\), show that \(\gamma '(t)=\lim _{s\to t}\frac {\gamma (s)-\gamma (t)}{s-t}\).
We compute that\begin{align*} \lim _{s\to t}\frac {\gamma (s)-\gamma (t)}{s-t} &=\lim _{s\to t}\biggl ( \frac {\re \gamma (s)-\re \gamma (t)}{s-t} +i\frac {\im \gamma (s)-\im \gamma (t)}{s-t}\biggr ). \end{align*}By linearity of limits
\begin{align*} \lim _{s\to t}\frac {\gamma (s)-\gamma (t)}{s-t} &=\left ( \lim _{s\to t}\frac {\re \gamma (s)-\re \gamma (t)}{s-t}\right )+i\left (\lim _{s\to t}\frac {\im \gamma (s)-\im \gamma (t)}{s-t}\right ) = (\re \gamma )'(t)+i(\im \gamma )'(t)\end{align*}as desired.
(Complex line integral.) Let \(\gamma \in C^1([a,b])\), \(\gamma :[a,b]\to \Omega \) for some \(\Omega \subseteq \C \), and let \(F:\Omega \to \C \) be continuous on \(\Omega \). We define
where we use complex multiplication in the second integral.
Let \(a<b\) be real numbers and let \(f:[a,b]\to \C \) be a continuous function.
Let \( \gamma :[0,1]\to \Omega \subset \R ^2\) be a \(C^1\) curve and let \(\vec F:\Omega \to \R ^2\) be a vector-valued function. Recall that we identify \(\R ^2\) with \(\C \), so that we identify \( \gamma =(\gamma _1,\gamma _2)\) with \(\gamma _1+i\gamma _2\) and \(\vec F=(F_1,F_2)\) with \(F=F_1+iF_2\).
Show that
where \(\nu =\begin {pmatrix}0&1\\-1&0\end {pmatrix}\tau \) is the unit rightward normal vector to \(\gamma \).
Let \(\gamma :[a,b]\to \Omega \subseteq \C \) be \(C^1\), where \(\Omega \) is open, and let \(f\) be holomorphic in \(\Omega \). Then
Give an example of a \(C^1\) curve \(\gamma \) and a \(C^1\) function \(f\) defined in an open neighborhood of \(\widetilde \gamma \) such that
Let \(f(z)=\overline {z}\). Then \(\frac {\partial f}{\partial z}=0\) and so the left hand side is zero, but \(\overline z\) is one-to-one and so the right hand side is not zero unless \(\gamma \) is closed; for example, if \(\gamma (t)=t\), \(a=0\), \(b=1\), then \(f(\gamma (b))-f(\gamma (a))=1\neq 0\).
Prove Proposition 2.1.6.
By the fundamental theorem of calculus, we have that\begin{align*}f(\gamma (b))-f(\gamma (a)) &=\bigl [\re f(\gamma (b))-\re f(\gamma (a))\bigr ] + i\bigl [\im f(\gamma (b))-\im f(\gamma (a))\bigr ] \\&= \int _a^b \frac {d}{dt} \re f(\gamma (t)) \,dt + i \int _a^b \frac {d}{dt} \im f(\gamma (t)) \,dt \\&= \int _a^b \frac {d}{dt} \re f(\gamma (t)) + i \frac {d}{dt} \im f(\gamma (t)) \,dt \\&= \int _a^b \frac {d}{dt} f(\gamma (t)) \,dt .\end{align*}By 841Memory 841 (with \(\gamma '(t)\) viewed as a vector in \(\R ^2\))
\begin{align*}\frac {d}{dt} \re f(\gamma (t)) &= \nabla (\re f)(\gamma (t)) \cdot \gamma '(t) \,dt .\end{align*}Let \(\gamma (t)=\gamma _1(t)+i\gamma _2(t)=(\gamma _1(t),\gamma _2(t))\) where \(\gamma _1\), \(\gamma _2\) are real valued functions. Then
\begin{align*}\frac {d}{dt} \re f(\gamma (t)) &= \p [(\re f)]{x}(\gamma (t))\,\gamma _1'(t) +\p [(\re f)]{y}(\gamma (t))\,\gamma _2'(t) .\end{align*}Similarly
\begin{align*}\frac {d}{dt} \im f(\gamma (t)) &= \p [(\im f)]{x}(\gamma (t))\,\gamma _1'(t) +\p [(\im f)]{y}(\gamma (t))\,\gamma _2'(t) \end{align*}and so
\begin{align*}\frac {d}{dt} f(\gamma (t)) &= \frac {d}{dt} \re f(\gamma (t)) + i \frac {d}{dt} \im f(\gamma (t)) \\&= \p [ f]{x}(\gamma (t))\,\gamma _1'(t) +\p [f]{y}(\gamma (t))\,\gamma _2'(t) .\end{align*}By 660Problem 660, and because \(f\) is holomorphic, we have that
\begin{align*}\frac {d}{dt} f(\gamma (t)) &= \p [ f]{z}(\gamma (t))\,\gamma _1'(t) +i\p [f]{z}(\gamma (t))\,\gamma _2'(t) \\&=\p [ f]{z}(\gamma (t))\,\gamma '(t) .\end{align*}Thus
\begin{align*}f(\gamma (b))-f(\gamma (a)) &= \int _a^b \frac {d}{dt} f(\gamma (t)) \,dt \\&= \int _a^b \p [ f]{z}(\gamma (t))\,\gamma '(t) \,dt .\end{align*}By definition
\begin{equation*}\oint _\gamma \frac {\partial f}{\partial z}\,dz = \int _a^b \p [f]{z}(\gamma (t))\,\gamma '(t)\,dt.\end{equation*}This completes the proof.
If \(\gamma :[a,b]\to \Omega \subseteq \C \) is a \(C^1\) curve and \(f:\Omega \to \C \) is continuous, then \(\displaystyle \left |\oint _\gamma f(z)\,dz\right |\leq \sup _{[a,b]} |f\circ \gamma | \cdot \ell (\gamma )=\sup _{\widetilde \gamma } |f| \cdot \ell (\gamma )\), where \(\ell (\gamma )=\int _a^b |\gamma '|\).
Prove Proposition 2.1.8.
By definition\begin{equation*}\oint _\gamma f(z)\,dz = \int _a^b f(\gamma (t))\,\gamma '(t)\,dt. \end{equation*}By 940Problem 940
\begin{align*} \biggl |\oint _\gamma f(z)\,dz\biggr | &\leq \int _a^b |f(\gamma (t))|\,|\gamma '(t)|\,dt \leq \sup _{[a,b]} |f\circ \gamma | \int _a^b |\gamma '(t)|\,dt. \end{align*}Recalling the definition of arc length completes the proof.
Let \(\Omega \subseteq \C \), let \(F:\Omega \to \C \) be continuous, let \(\gamma _1:[a,b]\to \Omega \) be a \(C^1\) curve, and let \(\varphi :[c,d]\to [a,b]\) be \(C^1\) and bijective. Define \(\gamma _2=\gamma _1\circ \varphi \).
If \(\varphi \) is strictly increasing, then \(\oint _{\gamma _1} F(z)\,dz=\oint _{\gamma _2} F(z)\,dz\).
In this problem we begin the proof of Proposition 2.1.9. Let \(\gamma _1:[a,b]\to \C \) be a \(C^1\) curve. Let \(\varphi :[c,d]\to [a,b]\) be a continuous bijection. Define \(\gamma _2=\gamma _1\circ \varphi \). Compute \(\gamma _2'(t)\) in terms of \(\gamma _1\), \(\gamma _1'\), \(\varphi \), and \(\varphi '\). Then show that \(\widetilde \gamma _1=\widetilde \gamma _2\). (Recall \(\widetilde \gamma \) denotes the image of \(\gamma \).)
Prove Proposition 2.1.9. Do not assume that \(F\) is holomorphic.
Let \(\gamma _1:[-a,a]\to \C \). Let \(\gamma _2:[-a,a]\to \C \) be given by \(\gamma _2(t)=\gamma _1(-t)\). Show that if \(F\) is continuous in a neighborhood of \(\widetilde \gamma _1\), then \(\oint _{\gamma _1} F(z)\,dz=-\oint _{\gamma _2} F(z)\,dz\).
Suppose that \(\gamma _1:[a,b]\to \Omega \subseteq \C \) is a simple closed \(C^1\) curve, and that \(\gamma _1'(a)=\gamma _1'(b)\). If \(z_0\in \widetilde \gamma _1\), show that there is a simple closed curve \(\gamma _2:[0,1]\to \C \) such that \(\gamma _2(c)=\gamma _2(d)=z_0\), \(\widetilde \gamma _2=\widetilde \gamma _1\), and \(\oint _{\gamma _1} F(z)\,dz=\oint _{\gamma _2} F(z)\,dz\) for every \(F\) continuous on \(\Omega \).
Prove that the previous problem still holds even if \(\gamma _1'(a)\neq \gamma _1'(b)\).
If \(\gamma _1:[a,b]\to \C \) is injective, and \(\gamma _2:[a,b]\to \C \) is a simple closed curve, then \(\widetilde \gamma _1\neq \widetilde \gamma _2\).
Given a set in \(C^1\) that can be written as the image of a \(C^1\) curve, and an orientation of that set, any two parameterizations of the set will yield the same line integrals.
More precisely, let \(\widetilde \gamma \subseteq \Omega \subseteq \C \). Suppose that there is at least one injective or simple closed \(C^1\) curve \(\gamma _1:[a,b]\to \Omega \) such that \(\widetilde \gamma _1=\widetilde \gamma \).
If \(\gamma _2:[c,d]\to \Omega \) is any other injective or simple closed \(C^1\) curve with \(\widetilde \gamma _2=\widetilde \gamma \), then either \(\oint _{\gamma _1} F(z)\,dz=\oint _{\gamma _2} F(z)\,dz\) for all functions \(F:\Omega \to \C \) continuous, or \(\oint _{\gamma _1} F(z)\,dz=-\oint _{\gamma _2} F(z)\,dz\) for all functions \(F:\Omega \to \C \) continuous.
Furthermore, if \(\gamma _1\) and \(\gamma _2\) are injective, if \(z_1\), \(z_2\in \widetilde \gamma \), and if \(\gamma _1^{-1}(z_1)<\gamma _1^{-1}(z_2)\) and \(\gamma _2^{-1}(z_1)<\gamma _2^{-1}(z_2)\), then \(\oint _{\gamma _1} F(z)\,dz=\oint _{\gamma _2} F(z)\,dz\) for all functions \(F:\Omega \to \C \) continuous.
Finally, if \(\gamma _1\) and \(\gamma _2\) are simple closed curves, if \(z_1\), \(z_2\), \(z_3\in \widetilde \gamma \), if \(\gamma _1(a)=\gamma _1(b)=\gamma _2(c)=\gamma _2(d)=z_3\), and if \(\gamma _1^{-1}(z_1)<\gamma _1^{-1}(z_2)\) and \(\gamma _2^{-1}(z_1)<\gamma _2^{-1}(z_2)\), then \(\oint _{\gamma _1} F(z)\,dz=\oint _{\gamma _2} F(z)\,dz\) for all functions \(F:\Omega \to \C \) continuous.
Let \(\gamma _1:[a,b]\to \C \) and \(\gamma _2:[c,d]\to \C \) be two curves. Suppose further that \(\widetilde \gamma _1=\widetilde \gamma _2\), \(\gamma _1(a)=\gamma _2(c)\), \(\gamma _1(b)=\gamma _2(d)\), and that \(\gamma _1\) and \(\gamma _2\) are injective. Show that there is a continuous strictly increasing function \(\varphi :[c,d]\to [a,b]\) such that \(\gamma _2=\gamma _1\circ \varphi \).
By definition \(\gamma _1:[a,b]\to \widetilde \gamma _1\) is a bijection. 880Memory 880 and 890Memory 890, we have that the inverse \(\gamma _1^{-1}\) is also continuous. Thus \(\varphi =\gamma _1^{-1}\circ \gamma _2\) is a continuous bijection from \([c,d]\) to \([a,b]\) that satisfies \(\gamma _2=\gamma _1\circ \varphi \). By 873Problem 873, and because \(\varphi (c)=\gamma _1^{-1}(\gamma _2(c))=a\), we have that \(\varphi \) is strictly increasing.
If \(\gamma _1:[a,b]\to \C \) and \(\gamma _2:[c,d]\to \C \) are simple closed curves rather than injective functions, with \(\widetilde \gamma _1=\widetilde \gamma _2\) and \(\gamma _1(a)=\gamma _1(b)=\gamma _2(c)=\gamma _2(d)\), is it necessarily the case that \(\gamma _2=\gamma _1\circ \varphi \) for a continuous strictly increasing function \(\varphi :[c,d]\to [a,b]\)?
No. Let \(\gamma _1(t)=e^{it}\) and let \(\gamma _2=e^{-it}\), both with domain \([-\pi ,\pi ]\). If \(\gamma _2(t)=\gamma _1(\varphi (t))\), then \(\varphi (t)=-t\) for all \(t\in (-\pi ,\pi )\), and so in particular \(\varphi \) cannot be strictly increasing.
Prove 1014Proposition 1014.
Let \(\gamma _1:[a,b]\to \C \) and \(\gamma _2:[c,d]\to \C \) be two \(C^1\) curves. Suppose that \(\gamma _1(b)=\gamma _2(c)\). Show that there is a \(C^1\) curve \(\gamma _3:[-1,1]\to \C \) such that \(\gamma _3\big \vert _{[-1,0]}\) is a reparameterization of \(\gamma _1\) and \(\gamma _3\big \vert _{[0,1]}\) is a reparameterization of \(\gamma _2\). (We will write \(\gamma _3=\gamma _1*\gamma _2\). This means that \(\widetilde \gamma _3=\widetilde \gamma _1\cup \widetilde \gamma _2\) and \(\oint _{\gamma _3} F(z)\,dz=\oint _{\gamma _1} F(z)\,dz+\oint _{\gamma _2} F(z)\,dz\) for all \(F\) continuous in a neighborhood of \(\widetilde \gamma _3\).)
The function\begin{equation*}\gamma _3(t)=\begin {cases} \gamma _1(b+(b-a)t^3), & -1\leq t\leq 0,\\ \gamma _2(c+(d-c)t^3),& 0\leq t\leq 1\end {cases}\end{equation*}satisfies the given conditions. Note in particular that \(\gamma _3'(0)=0\).
Let \(\Omega \), \(W\subseteq \C \) be open and let \(u:\Omega \to W\) be holomorphic. Let \(\gamma :[0,1]\to \Omega \) be a \(C^1\) closed curve. Let \(f:W\to \C \) be continuous. Show that
By definition\begin{align*}\oint _{u\circ \gamma } f(w)\,dw&=\int _0^1 f(u\circ \gamma (t)) \, (u\circ \gamma )'(t)\,dt, \\ \oint _\gamma f(u(z))\,\frac {\partial u}{\partial z}\,dz &=\int _0^1 f(u(\gamma (t))) \,\frac {\partial u}{\partial z}\big \vert _{z=\gamma (t)} \,\gamma '(t)\,dt.\end{align*}As in the proof of 970Problem 970, because \(u\) is holomorphic we have that \((u\circ \gamma )'(t)=\frac {\partial u}{\partial z}\big \vert _{z=\gamma (t)} \,\gamma '(t)\). This completes the proof.
I want to compute \(\int _{-1}^1 \frac {(t+i)^3}{(t+i)^4+1}dt\). A naïve student uses the \(u\)-substitution \(u=(t+i)^4\) and converts the integral to \(\int _{-4}^{-4} \frac {1}{4} \frac {1}{u+1} du=0\). But when I compute \(\int _{-1}^1 \frac {(t+i)^3}{(t+i)^4+1}dt\) using a numerical solver, I get \(-i\pi /2\). What went wrong?
If \((X,d)\) and \((Z,\rho )\) are metric spaces, \(p\in Z\), and \(f:Z\setminus \{p\}\to X\), we say that \(\lim _{z\to p}f(z)=\ell \) if, for all \(\varepsilon >0\), there is a \(\delta >0\) such that if \(z\in Z\) and \(0<\rho (z,p)<\delta \), then \(d(f(z),f(p))<\varepsilon \).
If \((X,d)\) and \((Z,\rho )\) are metric spaces and \(f:Z\to X\), we say that \(f\) is continuous at \(p\in Z\) if \(f(p)=\lim _{z\to p} f(z)\).
If \(\Omega \subset \R ^d\) is open, \(p\in \Omega \), and \(f:\Omega \to \R \) is a \(C^1\) function, then
where \(\cdot \) denotes the dot product and \(\nabla f(p)\) is the vector of partial derivatives \((\frac {\partial f}{\partial x_1},\p [f]{x_2},\dots ,\p [f]{x_d})\) evaluated at the point \(p\).
The open disc (or ball) in \(\C \) of radius \(r\) and center \(p\) is \(D(p,r)=B(p,r)=\{z\in \C :|z-p|<r\}\). The closed disc (or ball) in \(\C \) of radius \(r\) and center \(p\) is \(\overline D(p,r)=\overline B(p,r)=\{z\in \C :|z-p|\leq r\}\).
Let \(\gamma :[0,1]\to \C \) be a (parameterization of a) nondegenerate scalene triangle of your choice. You don’t need to find a formula for \(\gamma (t)\). Sketch the trace of \(\gamma \) and of \(f\circ \gamma \) for the following choices of \(f\):
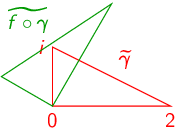
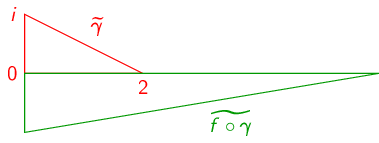
We chose \(\gamma \) to be a parameterization of:
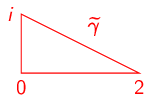
Then:
- (a)
- \(f(z)=z-3+i\)
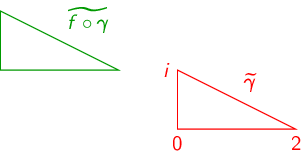
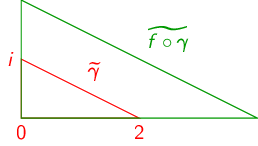
- (b)
- \(f(z)=(\frac {1}{2}+\frac {\sqrt {3}}{2}i)z\)
- (c)
- \(f(z)=2z\)
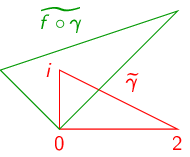
- (d)
- \(f(z)=(1+i)z\)
- (e)
- \(f(z)=(1+i)z-3+i\)
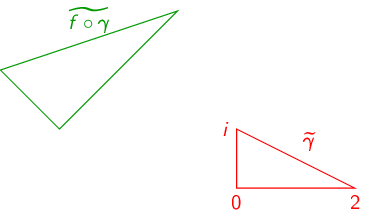
- (f)
- \(f(z)=\bar z\)
- (g)
- \(f(z)=z+2\bar z\)
Let \(p\in \Omega \subseteq \C \), where \(\Omega \) is open. Let \(f:\Omega \to \C \). Suppose that \(\lim _{z\to p} \frac {f(z)-f(p)}{z-p}\) exists. Then we say that \(f\) has a complex derivative at \(p\) and write \(f'(p)=\lim _{z\to p} \frac {f(z)-f(p)}{z-p}\).
Show that \(f(z)=\overline z\) does not have a complex derivative.
Show that if \(f\) is constant then \(f'(p)=0\) for all \(p\).
Show that if \(f(z)=z\) then \(f'(p)=1\) for all \(p\).
If \(\Omega \subseteq \C \) is open, \(p\in \Omega \), and \(f\), \(g:\Omega \setminus \{p\}\to \C \) are such that \(\lim _{z\to p} f(z)\) and \(\lim _{z\to p} g(z)\) exist (as complex numbers), then we have the usual formulas
and (if \(\lim _{z\to p} g(z)\neq 0\))
If \(f\) has a complex derivative at \(p\), then \(f\) is continuous at \(p\).
If \(\Omega \subseteq \C \) is open, \(p\in \Omega \), and \(f\), \(g:\Omega \to \C \) are functions that have complex derivatives at \(p\), and if \(\alpha \), \(\beta \in \C \), then \(\alpha f+\beta g\) and \(fg\) have complex derivatives at \(p\) and
If in addition \(g(p)\neq 0\) then \(f/g\) has a complex derivative at \(p\) and
If \(\Omega \subseteq \C \) and \(W\subseteq \C \) are open, \(p\in \Omega \), \(f:\Omega \setminus \{p\}\to W\) is such that \(L=\lim _{z\to p} f(z)\) exists, \(L\in W\), and \(g:W\to \C \) is continuous at \(L\), then
Observe that we do require \(g(L)\) to exist, not only \(\lim _{w\to L} g(w)\).
Suppose that \(f\) has a complex derivative at \(p\). Then \(\frac {\partial f}{\partial z}\big \vert _{z=p}=f'(p)\).
Suppose that \(f\) has a complex derivative at \(p\). Prove Theorem 2.2.2 and also show that \(\frac {\partial f}{\partial \bar z}\big \vert _{z=p}=0\).
First, observe that\begin{equation*}\frac {\partial f}{\partial x}\Big \vert _{x+iy=p} = \lim _{\substack {s\to 0\\s\in \R }} \frac {f(p+s)-f(p)}{s}.\end{equation*}Because \(f'(p)=\lim _{z\to p}\frac {f(z)-f(p)}{z-p}\), by definition of limit, for every \(\varepsilon >0\) there is a \(\delta >0\) such that if \(z\in \C \) and \(0<|z|<\delta \) then \(\left |\frac {f(p+z)-f(p)}{z}-f'(p)\right |<\varepsilon \). This in particular is true if \(s\) is real and \(0<|s|<\delta \), as real numbers are complex numbers. Thus we must have that \(f'(p)=\frac {\partial f}{\partial x}\big \vert _{x+iy=p}\).
Similarly,
\begin{equation*}\frac {\partial f}{\partial y}\Big \vert _{x+iy=p} = \lim _{\substack {s\to 0\\s\in \R }} \frac {f(p+is)-f(p)}{s} = i\lim _{\substack {s\to 0\\s\in \R }} \frac {f(p+is)-f(p)}{is}=if'(p) .\end{equation*}We thus compute
\begin{equation*}\frac {\partial f}{\partial z}\bigg \vert _{z=p} =\frac {1}{2}\biggl (\p [f]{x}\bigg \vert _{x+iy=p}+\frac {1}{i} \p [f]{y}\bigg \vert _{x+iy=p}\biggr ) =f'(p)\end{equation*}and
\begin{equation*}\frac {\partial f}{\partial \bar z}\bigg \vert _{z=p} =\frac {1}{2}\biggl (\p [f]{x}\bigg \vert _{x+iy=p}-\frac {1}{i} \p [f]{y}\bigg \vert _{x+iy=p}\biggr ) =0.\end{equation*}
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be continuous. Let \(W\subseteq \C \) be open. Let \(g:W\to \Omega \) be continuous. Then \(f\circ g:W\to \C \) is continuous. Suppose that \(z_0\in W\) and that \(g'(z_0)\) and \(f'(g(z_0))\) exist (in the sense of limits as above). Show that \((f\circ g)'(z_0)\) exists and that \((f\circ g)'(z_0)=f'(g(z_0))\,g'(z_0)\).
Let\begin{equation*}F(z)=\begin {cases} \frac {f(z)-f(g(t_0))}{z-g(t_0)},& z\in \Omega \setminus \{g(t_0)\},\\ f'(g(t_0)),&z=g(t_0).\end {cases}\end{equation*}Because \(f'(g(t_0))\) exists, \(\lim _{z\to g(t_0)} F(z)=F(g(t_0))\).
Now,
\begin{align*}\lim _{s \to t_0} \frac {f\circ g(s)-f\circ g(t_0)}{s-t_0} &=\lim _{s \to t_0} F(g(s)) \frac {g(s)-g(t_0)}{s-t_0} \\&=f'(g(t_0))\,g'(t_0).\end{align*}
(Generalization.) Suppose that \(\Omega \subseteq \C \) is open and that \(f\) is \(C^1\) on \(\Omega \). Let \(p\in \Omega \) and suppose \(\p [f]{\bar z}\big \vert _{z=p}=0\). Then \(f\) has a complex derivative at \(p\) and \(f'(p)=\frac {\partial f}{\partial z}\big \vert _{z=p}\).
Prove this generalization of Theorem 2.2.1.
Let \(F:\R ^2\to \R ^2\). Suppose that \(\nabla F_1\) and \(\nabla F_2\) are constants. Show that \(F(x,y)=F(0,0)+(\partial _1 F_1,\partial _1 F_2)x+(\partial _2 F_1,\partial _2 F_2)y\) for all \((x,y)\in \R ^2\).
We compute that (for \(j=1\) or \(j=2\))\begin{align*} F_j(x,y)&= F_j(x,y)-F_j(x,0)+F_j(x,0)-F_j(0,0)+F_j(0,0) \\&= F_j(0,0)+\int _0^x \frac {\partial }{\partial s} F_j(s,0)\,ds + \int _0^y \p {t} F_j(x,t)\,dt. \end{align*}Because the integrands are constants, they may easily be evaluated to yield the desired result.
Suppose that \(f:\C \to \C \). Suppose that \(f'\) exists everywhere and is a constant. Show that \(f(z)=f(0)+f'(0)z\) for all \(z\in \C \). Conclude that if \(z\), \(\omega \), \(w\in \C \) with \(\omega \neq z\neq w\), then \(\frac {|f(\omega )-f(z)|}{|\omega -z|}=\frac {|f(w)-f(z)|}{|w-z|}\).
Define \(\gamma :[0,1]\to \Omega \) by \(\gamma (t)=p+t(z-p)\). Then by Proposition 2.1.6, we have that\begin{equation*}f(\zeta )-f(p)=\oint _{\gamma } \frac {\partial f}{\partial z}\,dz.\end{equation*}By Theorem 2.2.2 ( 1110Problem 1110), \(\frac {\partial f}{\partial z}=f'(z)=f'(0)\) because \(f'\) is constant. The result follows by definition of line integral.
Let \(F:\R ^2\to \R ^2\). Let \(F=(F_1,F_2)\). Suppose that \(\nabla F_1\) and \(\nabla F_2\) exist everywhere and are constant. Show that if \(C\) is a circle, then \(F(C)\) is an ellipse, and if \(S\) is a square, show that \(F(S)\) is a parallelogram.
Let \(f:\C \to \C \). Suppose that \(f'\) exists everywhere and is constant. Show that if \(C\) is a circle, then \(F(C)\) is also a circle, and if \(S\) is a square, show that \(F(S)\) is also a square.
1. Let \(z_0\in \Omega \subseteq \C \) for some open set \(\Omega \). Let \(f:\Omega \to \C \). Let \(w_1\), \(w_2\in \C \) with \(w_1\), \(w_2\neq 0\). Suppose that \(f'(z_0)\) exists. Then \(\lim _{t\to 0} \frac {|f(z_0+tw_1)-f(z_0)|}{|tw_1|}=\lim _{t\to 0} \frac {|f(z_0+tw_2)-f(z_0)|}{|tw_2|}\).
Prove Theorem 2.2.3.1. How does this relate to the result of 1150Problem 1150?
Let \(z_0\in \Omega \subseteq \C \) for some open set \(\Omega \). Let \(f:\Omega \to \C \). Suppose that \(\lim _{t\to 0} \frac {|f(z_0+tw_1)-f(z_0)|}{|tw_1|}=\lim _{t\to 0} \frac {|f(z_0+tw_2)-f(z_0)|}{|tw_2|}\) for all \(w_1\), \(w_2\in \C \setminus \{0\}\). Then either \(f'(z_0)\) exists or \((\overline f)'(z_0)\) exists.
If \(z\in \C \setminus \{0\}\), define \(\hat z=\frac {1}{|z|}z\).
If \(z\in \C \setminus \{0\}\), then \(\hat z=e^{i\theta }\) for some real number \(\theta \), and if \(\hat z=e^{i\psi }\) then \(\theta -\psi \) is an integer multiple of \(2\pi \).
Let \(z\), \(w\in \C \setminus \{0\}\). Let \(\angle (z,w)\) be the directed angle from \(z\) to \(w\) (that is, the angle between the line from \(0\) to \(z\) and the line from \(0\) to \(w\), chosen such that you move from \(z\) to \(w\) counterclockwise).
Show that \(\exp (i\angle (z,w)) = \frac {\hat w}{\hat z}\). (This provides an algebraically simpler but geometrically les intuitive definition of the directed angle, as the unique real number in \([0,2\pi )\) such that the above equation is true.)
Let \(z_0\in \Omega \subseteq \C \) for some open set \(\Omega \). Let \(f:\Omega \to \C \). We say that \(f\) preserves angles at \(z_0\) if, for all \(w_1\), \(w_2\in \C \setminus \{0\}\), we have that
and in particular that \(f(z_0+tw_1)-f(z_0)\) and \(f(z_0+tw_2)-f(z_0)\) are not zero when \(t\) is sufficiently close to \(0\). [This is not the definition in the book.]
2. If \(f'(z_0)\) exists and is not zero, then \(f\) preserves angles at \(z_0\).
Prove Theorem 2.2.3.2.
If \(f\) is \(C^1\) and preserves angles at \(z_0\), and if the Jacobian matrix of \(f\) at \(z_0\) is nonsingular, then \(f'(z_0)\) exists.
If \(f\) is \(C^1\) and preserves angles at \(z_0\), and if the Jacobian matrix of \(f\) at \(z_0\) is singular, must \(f'(z_0)\) exist?
Consider the following figures. On the left is shown the traces of \(\gamma _j\) for several values of \(j\). On the right is shown the traces of \(f\circ \gamma _j\), \(g\circ \gamma _j\), or \(h\circ \gamma _j\) for the same \(\gamma _j\). You are given that exactly two of the quantities \(f'(0)\), \(g'(0)\), and \(h'(0)\) exist and that exactly one of those quantities is zero. Based on the images, which function do you think has nonzero derivative, which has zero derivative, and which does not have a derivative?
Let \(f(x)=x^2\sin (1/x)\) if \(x\neq 0\) and let \(f(0)=0\). Then \(f\) is continuous on \((-\infty ,\infty )\), continuously differentiable on \((-\infty ,0)\) and \((0,\infty )\), and \(f'(0)\) exists, but the limit \(\lim _{x\to 0} f'(x)\) does not exist.
Suppose that \(a<p<b\) and let \(H:(a,b)\to \R \) be continuous. Suppose that \(H\) is differentiable on both \((a,p)\) and \((p,b)\), and that \(\lim _{x\to p} H'(x)=h\) for some \(h\in \R \). Then \(H'(p)\) exists and \(H'(p)=\lim _{x\to p} H'(x)\).
Suppose that there are two \(C^1\) functions \(g\) and \(h\) defined in an open rectangle or disc \(\Omega \) such that \(\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h\). Then there is a function \(f\in C^2(\Omega )\) such that \(\frac {\partial f}{\partial y}=g\) and \( \frac {\partial f}{\partial x}=h\).
Let \(\Omega \subset \R ^2\) be an open rectangle or disc and let \(P\in \Omega \). Suppose that there are two functions \(g\) and \(h\) that are continuous on \(\Omega \), continuously differentiable on \(\Omega \setminus \{P\}\), and such that \(\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h\) on \(\Omega \setminus \{P\}\) for some \(P\in \Omega \). Then there is a function \(f\in C^1(\Omega )\) such that \(\frac {\partial f}{\partial y}=g\) and \( \frac {\partial f}{\partial x}=h\) everywhere in \(\Omega \) (including at \(P\)).
Prove Theorem 2.3.2.
Let \(P=(x_0,y_0)\) and let \(f(x,y)=\int _{x_0}^x h(s,y_0)\,ds+\int _{y_0}^y g(x,t)\,dt\). Observe that if \((x,y)\in \Omega \) then so is \((s,y_0)\) and \((x,t)\) for all \(s\) between \(x_0\) and \(x\) and all \(t\) between \(y_0\) and \(y\). Thus \(g\) and \(h\) are defined at all required values. Because \(g\) and \(h\) are continuous, the integrals exist.Furthermore, I claim \(f\) is continuous. Let \((x,y)\in \Omega \) and let \(\delta _1>0\) be such that \(B((x,y),\delta _1)\subset \Omega \). By continuity of \(g\) and \(h\) and compactness of \(\overline B((x,y),\delta _1/2)\), \(g\) and \(h\) are bounded on \(\overline B((x,y),\delta _1/2)\). If \((\xi ,\eta )\in B((x,y),\delta _1/2)\), then
\begin{align*} f(\xi ,\eta )-f(x,y) &= \int _x^{\xi } h(s,y_0)\,ds + \int _y^{\eta } g(\xi ,t)\,dt + \int _{y_0}^y g(\xi ,t)-g(x,t)\,dt \end{align*}and so
\begin{align*} |f(\xi &,\eta )-f(x,y)| \\&\leq |\xi -x|\sup _{\overline B((x,y),\delta _1/2)} |h| +|\eta -y|\sup _{\overline B((x,y),\delta _1/2)} |g| + \biggl |\int _{y_0}^y g(x,t)-g(\xi ,t)\,dt\biggr | .\end{align*}Furthermore, \(g\) must be uniformly continuous on \(\overline B((x,y),\delta _1/2)\). Choose \(\varepsilon >0\) and let \(\delta _2\) be such that if \(|(x,t)-(\xi ,t)|<\delta _2\) then \(|g(x,t)-g(\xi ,t)|<\varepsilon \). We then have that
\begin{align*} |f(x&,y)-f(\xi ,\eta )| \leq |\xi -x|\sup _{\overline B((x,y),\delta _1/2)} |h| +|\eta -y|\sup _{\overline B((x,y),\delta _1/2)} |g| +|y_0-y|\varepsilon .\end{align*}There is then a \(\delta _3>0\) such that if \(|(\xi ,\eta )-(x,y)|<\delta _3\) then \(|f(x,y)-f(\xi ,\eta )|<(1+|y_0-y|)\varepsilon \), and so \(f\) is continuous at \((x,y)\), as desired.
By the fundamental theorem of calculus, we have that \(\frac {\partial f}{\partial y}=g\) everywhere in \(\Omega \), including at \((x,y)=(x_0,y_0)=P\).
Furthermore, by 770Problem 770 and the fundamental theorem of calculus, we have that if \(x\neq x_0\) then
\begin{equation*}\frac {\partial f}{\partial x}(x,y) =h(x,y_0)+\int _{y_0}^y \frac {\partial g}{\partial x}(x,t)\,dt.\end{equation*}Again because \(x\neq x_0\), we have that \(\p [g]{x}(x,t)=\p [h]{t}(x,t)\) and so by the fundamental theorem of calculus \(\p [f]{x}=h\) provided \(x\neq x_0\).
We need only show that \(\p [f]{x}=h\) even if \(x=x_0\). Fix a \(y\) and let \(F_y(x)=f(x,y)\). Then \(I=\{x\in \R :(x,y)\in \Omega \}\) is an open interval. We need only consider the case where \(I\neq \emptyset \). Then \(F_y\) is continuous on \(I\), \(F_y'(x)=h(x,y)\) for all \(x\neq x_0\), and \(\lim _{x\to x_0} F_y'(x)=h(x_0,y)\) because \(h\) is continuous. Thus by Lemma 2.3.1, \(F_y'(x_0)=h(x_0,y)\) and so \(\p [f]{x}=h\) even if \(x=x_0\).
Must the function \(f\) in Theorem 2.3.2 be \(C^2\) (that is, must \(g\) and \(h\) be continously differentiable at \(P\) as well as elsewhere in \(\Omega \)? If so, prove it; if not, give a counterexample.
Let \(P\in \Omega \), where \(\Omega \) is an open rectangle or disc. Suppose that \(f\) is continuous on \(\Omega \) and holomorphic on \(\Omega \setminus \{P\}\). Then there is a function \(F\) that is holomorphic on all of \(\Omega \) (including \(P\)) such that \(\frac {\partial F}{\partial z} = f\).
Prove Theorem 2.3.3.
Let \(f=u+iv\) where \(u\) and \(v\) are real valued; then by definition \(u\), \(v\) are continuous on \(\Omega \) and \(C^1\) on \(\Omega \setminus \{P\}\).Then by the Cauchy-Riemann equations, we have that \(\p [u]{x}=\p [v]{y}\). Therefore, by Theorem 2.3.2, there is a \(V\in C^1(\Omega )\) such that \(\p [V]{y}=u\) and \(\p [V]{x}=v\) in all of \(\Omega \). Similarly, \(\p [u]{y}=\p [(-v)]{x}\), and so there is a \(U\in C^1(\Omega )\) such that \(\p [U]{x}=u\) and \(\p [U]{y}=-v\).
Let \(F=U+iV\). Then
\begin{equation*}\p [F]{z} = \frac {1}{2}\biggl (\p [F]{x}+\frac {1}{i}\p [F]{y}\biggr ) =\frac {1}{2}\biggl (u+iv+\frac {1}{i}(-v+iu)\biggr )=f \end{equation*}and
\begin{equation*}\p [F]{\bar z} = \frac {1}{2}\biggl (\p [F]{x}-\frac {1}{i}\p [F]{y}\biggr ) =\frac {1}{2}\biggl (u+iv-\frac {1}{i}(-v+iu)\biggr )=0 \end{equation*}in \(\Omega \), as desired.
Is the previous problem true if we relax the assumption that \(f\) is continuous at \(P\) (and that \(\p [F]{z}=f\) at \(P\))?
No. Let \(\Omega =D(0,2)\) and let \(P=0\). Then \(f(z)=1/z\) is holomorphic on \(\Omega \setminus \{P\}\) (see 620Problem 620) and by Problem 2.4a in your book, if \(\gamma (t)=e^{it}\), \(0\leq t\leq 2\pi \), then \(\oint _{\gamma } f(z)\,dz=2\pi i\).But if \(F\) is holomorphic in \(\Omega \setminus \{P\}\) and \(F'=f\), then by 970Problem 970
\begin{align*}\oint _\gamma f(z)\,dz &= \oint _\gamma \frac {\partial F}{\partial z} \,dz=F(\gamma (2\pi ))-F(\gamma (0))=F(1)-F(1)=0.\end{align*}This is a contradiction; therefore, no such \(F\) can exist.
In \(\C \), \(\overline D(P,r)\) is the closure of \(D(P,r)\).
In \(\C \), \(\partial D(P,r)=\partial \overline D(P,r)=\{z\in \C :|z-P|=r\}\).
[The Cauchy integral theorem.] Let \(f\) be holomorphic in \(D(P,R)\). Let \(\gamma :[a,b]\to D(P,R)\) be a closed curve. Then \(\oint _\gamma f(z)\,dz=0\).
Prove the Cauchy integral theorem.
[The Cauchy integral formula.] Let \(\Omega \subseteq \C \) be open and let \(\overline D(z_0,r)\subset \Omega \). Let \(f\) be holomorphic in \(\Omega \) and let \(z\in D(z_0,r)\). Then
where \(\gamma (t)=z_0+re^{it}\), \(0\leq t\leq 2\pi \), is the parametrization of \(\partial D(z_0,r)\) traversed once counterclockwise.
The Cauchy integral formula is true in the special case where \(f(\zeta )=1\) for all \(\zeta \in \C \).
Let \(\gamma :[a,b]\to K\) be a \(C^1\) curve for some set \(K\subseteq \C \) (not necessarily open). Let \(V\subseteq \C \) be either open or compact and let \(f: K\times V\to \C \) be continuous. Let \(F:V\to \C \) be defined by
Show that \(F\) is continuous on \(V\).
In this problem we will begin the proof of Lemma 2.4.1 (and thus ultimately of Theorem 2.4.2). Let \(\gamma :[a,b]\to K\) be a \(C^1\) curve for some set \(K\subseteq \C \) (not necessarily open). Let \(W\subseteq \C \) be open and let \(f: K\times W\to \C \) be continuous. Suppose that the functions \(\frac {\partial f}{\partial x}\) and \(\frac {\partial f}{\partial y}\) given by \(\frac {\partial f}{\partial x}(\zeta ,x+iy)=\frac {\partial }{\partial x} f(\zeta ,x+iy)\) and \(\frac {\partial f}{\partial y}(\zeta ,x+iy)=\frac {\partial }{\partial y} f(\zeta ,x+iy)\) are continuous on \(K\times W\). Show that
for all \(z=x+iy\in W\).
Prove Lemma 2.4.1. Hint: Start by proving Lemma 2.4.1 in the special case \(z=z_0\). Computing \(\re \oint _\gamma \frac {1}{\zeta -z}\,d\zeta \) and \(\im \oint _\gamma \frac {1}{\zeta -z}\,d\zeta \) directly from the definition of line integral is very difficult if \(z\neq z_0\). Instead compute the derivatives of \(G(z)= \oint _\gamma \frac {1}{\zeta -z}\,d\zeta \) and use the known value of \(\oint _\gamma \frac {1}{\zeta -z_0}\,d\zeta \).
\(\oint _\gamma \frac {1}{\zeta -z_0}\,d\zeta =1\) (this is a routine computation).If \(\zeta \neq x+iy\), then
\begin{align*} \p {x} \frac {1}{\zeta -(x+iy)} &=\p {x}\frac {\overline \zeta -x+iy}{(\re \zeta -x)^2+(\im \zeta -y)^2} \\&=\frac {-|\zeta -(x+iy)|^2+(\overline \zeta -x+iy)(2(\re \zeta -x))}{|\zeta -(x+iy)|^4} \\&=\frac {-|\zeta -(x+iy)|^2+(\overline \zeta -x+iy)((\overline \zeta -x+iy)+(\zeta -x-iy))}{(\zeta -x-iy)^2(\overline \zeta -x+iy)^2} \\&= \frac {1}{(\zeta -(x+iy))^2} .\end{align*}Now, by the previous problem, if \(x+iy\in D(P,r)\), then
\begin{align*} \frac {\partial }{\partial x} \oint _\gamma \frac {1}{\zeta -(x+iy)}\,d\zeta &= \oint _\gamma \p {x}\frac {1}{\zeta -(x+iy)}\,d\zeta \\&= \oint _\gamma \frac {1}{(\zeta -(x+iy))^2}\,d\zeta .\end{align*}Let \(F(\zeta )=\frac {-1}{\zeta -(x+iy)}\). By 620Problem 620 and the chain rule we have that \(\p {\zeta } F(\zeta )=\frac {1}{(\zeta -(x+iy))^2}\). Thus
\begin{align*} \frac {\partial }{\partial x} \oint _\gamma \frac {1}{\zeta -(x+iy)}\,d\zeta &= \oint _\gamma \p {\zeta }\frac {-1}{\zeta -(x+iy)}\,d\zeta \end{align*}which by 970Problem 970 is zero because \(\gamma \) is a closed curve.
Similarly
\begin{align*} \frac {\partial }{\partial y} \oint _\gamma \frac {1}{\zeta -(x+iy)}\,d\zeta &= 0 \end{align*}for all \(x+iy\in D(z_0,r)\). Thus \(\oint _\gamma \frac {1}{\zeta -(x+iy)}\,d\zeta \) (regarded as a function of \(x+iy\)) must be a constant; since it equals \(1\) at \(x+iy=z_0\), it must be \(1\) everywhere.
Let \(\gamma (t)=z_0+re^{i t}\), \(0\leq t\leq 2\pi \). Let \(n\) be an integer. Let \(z\in D(z_0,r)\). Show that \(\oint _\gamma (\zeta -z)^n\,d\zeta =0\) if \(n\neq -1\).
By 580Problem 580 and 620Problem 620, and by the chain rule (Problem 1.49), if \(n\neq -1\) then\begin{equation*}(\zeta -z)^n=\frac {1}{n+1} \frac {\partial }{\partial \zeta }(\zeta -z)^{n+1}.\end{equation*}Thus
\begin{align*}\oint _\gamma (\zeta -z)^n\,d\zeta &= \oint _\gamma \frac {1}{n+1} \frac {\partial }{\partial \zeta }(\zeta -z)^{n+1}\,d\zeta =\frac {(\gamma (2\pi )-z)^{n+1}}{n+1} -\frac {(\gamma (0)-z)^{n+1}}{n+1} =0\end{align*}
Show that if \(n\geq 0\) and \(\gamma \) is as in the previous problem, then
(As we have not yet proven the Cauchy integral formula, do not cite the Cauchy integral formula to perform this computation.)
If \(n=0\) then the result follows from Lemma 2.4.1. Otherwise, by the binomial theorem\begin{equation*}\zeta ^n=[(\zeta -z)+z]^n = \sum _{k=0}^n \binom {n}{k} z^{k}(\zeta -z)^{n-k}.\end{equation*}Thus
\begin{equation*}\oint _\gamma \frac {\zeta ^n}{\zeta -z}\,d\zeta =\sum _{k=0}^n \binom {n}{k}z^{k}\oint _\gamma (\zeta -z)^{n-k-1}\,d\zeta .\end{equation*}If \(k<n\) then the integral is zero, while if \(k=n\) then the integral is \(2\pi i\) by Lemma 2.4.1, as desired.
Let \(p\) be a holomorphic polynomial. Find \(\frac {1}{2\pi i}\oint _\gamma \frac {p(\zeta )}{\zeta -z}\,d\zeta \). (As we have not yet proven the Cauchy integral formula, do not cite the Cauchy integral formula to perform this computation.)
[The Cauchy integral formula.] Let \(\Omega \subseteq \C \) be open and let \(\overline D(z_0,r)\subset \Omega \). Let \(f\) be holomorphic in \(\Omega \) and let \(z\in D(z_0,r)\). Then
Prove Theorem 2.4.2. Hint: Let \(h(\zeta )=\frac {f(\zeta )-f(z)}{\zeta -z}\) if \(\zeta \neq z\). How should you define \(h(z)\)? What can you say about the behavior of \(h\) at \(z\) and in \(\Omega \setminus \{z\}\)?
Prove the previous result without using 1230Problem 1230.
We define \(\oint _{\partial D(P,r)} f(z)\,dz=\oint _\gamma f(z)\,dz\), where \(\gamma \) is a counterclockwise simple parameterization of \(\partial D(P,r)\).
Let \(f\) be continuous on \(\overline D(P,r)\) and holomorphic in \(D(P,r)\). Show that \(f(z)=\oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta \) for all \(z\in D(P,r)\).
Let \(f\) and \(g\) be holomorphic in \(D(P,r)\) and continuous on \(\overline D(P,r)\). Suppose that \(f(\zeta )=g(\zeta )\) for all \(\zeta \in \partial D(P,r)\). Show that \(f(z)=g(z)\) for all \(z\in D(P,r)\).
Let \(\Omega =D(P,\tau )\setminus \overline D(P,\sigma )\) for some \(P\in \C \) and some \(0<\sigma <\tau \). Let \(\sigma <r<R<\tau \) and let \(\gamma _r\), \(\gamma _R\) be the counterclockwise parameterizations of \(\partial D(P,r)\), \(\partial D(P,R)\). Suppose that \(f\) is holomorphic in \(\Omega \). Then \(\oint _{\gamma _r} f=\oint _{\gamma _R} f\).
Prove Proposition 2.6.6. Hint: Define \(\gamma _s\) in the natural way and find a function \(h\) such that \(\frac {d}{ds}\oint _{\gamma _s} f=\oint _{\gamma _s} h\).
Let \(a<b\), \(c<d\). Let \(\Omega \subseteq \C \) be open. Let \(\gamma _c\), \(\gamma _d:[a,b]\to \Omega \) be two \(C^1\) curves with the same endpoints (so \(\gamma _c(a)=\gamma _d(a)\), \(\gamma _c(b)=\gamma _d(b)\)).
We say that \(\gamma _c\) and \(\gamma _d\) are \(C^1\)-homotopic in \(\Omega \) if there is a function \(\Gamma \) such that:
Let \(a<b\), \(c<d\). Let \(\Omega \subseteq \C \) be open. Let \(\gamma _c\), \(\gamma _d:[a,b]\to \Omega \) be two closed \(C^1\) curves.
We say that \(\gamma _c\) and \(\gamma _d\) are \(C^1\)-homotopic in \(\Omega \) if there is a function \(\Gamma \) such that:
Show that the assumption that \(\Gamma \) be \(C^1\) in the first variable is unnecessary: if \(\gamma _c\) and \(\gamma _d\) are \(C^1\) and there is a function \(\Gamma \) satisfying all of the above conditions except that \(\Gamma \) is not \(C^1\) in the first variable, then \(\Gamma \) may be perturbed slightly to yield a \(C^1\) function. (In fact we may require the second derivative \(\frac {\partial ^2 \Gamma }{\partial s\partial t}\) to be continuous as well.)
Let \(\Omega =D(P,\tau )\setminus \overline D(P,\sigma )\) for some \(P\in \C \) and some \(0<\sigma <\tau \). Let \(\sigma <r<R<\tau \) and let \(\gamma _r\), \(\gamma _R\) be the counterclockwise parameterizations of \(\partial D(P,r)\), \(\partial D(P,R)\). Show that \(\gamma _r\) and \(\gamma _R\) are homotopic in \(\Omega \).
Let \(\Omega \subseteq \C \) be an open set and let \(f:\Omega \to \C \) be holomorphic.
Let \(a<b\), \(c<d\), and let \(\Gamma :[a,b]\times [c,d]\to \Omega \) be continuous.
Assume that, if \(s\in [c,d]\), then \(\gamma _s:[a,b]\to \Omega \) given by \(\gamma _s(t)=\Gamma (t,s)\) is a \(C^1\) curve.
Further assume that the function \(\frac {\partial \Gamma }{\partial t}\) (with \(\frac {\partial \Gamma }{\partial t}(a,s)\) and \(\frac {\partial \Gamma }{\partial t}(b,s)\) given by one-sided derivatives) is also continuous on \([a,b]\times [c,d]\).
Show that the function \(I(s)=\oint _{\gamma _s} f\) is continuous on \([c,d]\).
By definition of line integral,\begin{equation*}\oint _{\gamma _s} f = \int _a^b f(\Gamma (t,s))\,\p {t}\Gamma (t,s)\,dt.\end{equation*}By 760Problem 760, if \(c\leq s\leq d\) then \(\oint _{\gamma _s} f\) is continuous (as a function of \(s\)) at \(s\).
Let \(\Omega \), \(f\), and \(\Gamma \) be as in the previous problem. Assume that \(\frac {\partial \Gamma }{\partial s}\) and \(\frac {\partial ^2 \Gamma }{\partial s\,\partial t}\) exist and are continuous on \([a,b]\times (c,d)\).
Show that
By definition of line integral,\begin{equation*}\oint _{\gamma _s} f = \int _a^b f(\Gamma (t,s))\,\p {t}\Gamma (t,s)\,dt.\end{equation*}By 770Problem 770,
\begin{equation*}\frac {d}{ds}\oint _{\gamma _s} f = \int _a^b \p {s}\biggl (f(\Gamma (t,s))\,\p {t}\Gamma (t,s)\biggr )\,dt.\end{equation*}By the product rule and problem 1120Problem 1120,
\begin{align*}\frac {d}{ds}\oint _{\gamma _s} f &= \int _a^b f'(\Gamma (t,s))\,\p {s}\Gamma (t,s)\,\p {t}\Gamma (t,s) +f(\Gamma (t,s))\,\frac {\partial ^2}{\partial s\,\partial t} \Gamma (t,s) \,dt.\end{align*}By Clairaut’s theorem and the product rule,
\begin{equation*}\frac {d}{ds}\oint _{\gamma _s} f = \int _a^b\p {t}\biggl (f(\Gamma (t,s))\,\p {s}\Gamma (t,s)\biggr )\,dt.\end{equation*}By the fundamental theorem of calculus,
\begin{align*}\frac {d}{ds}\oint _{\gamma _s} f &= \biggl (f(\Gamma (b,s))\,\p {s}\Gamma (b,s)\biggr ) - \biggl (f(\Gamma (a,s))\,\p {s}\Gamma (a,s)\biggr ) \end{align*}as desired.
Let \(\Omega \) be an open set, let \(f:\Omega \to \C \) be holomorphic, and let \(\gamma _c\), \(\gamma _d:[a,b]\to \Omega \) be two curves with the same endpoints that are homotopic in \(\Omega \). Suppose that the homotopy \(\Gamma \) between \(\gamma _c\) and \(\gamma _d\) satisfies the conditions of 1381Problem 1381 and 1382Problem 1382. Show that
By 1382Problem 1382\begin{equation*}\frac {d}{ds}\oint _{\gamma _s} f = \biggl (f(\Gamma (b,s))\,\p {s}\Gamma (b,s)\biggr )- \biggl (f(\Gamma (a,s))\,\p {s}\Gamma (a,s)\biggr ) .\end{equation*}By definition of homotopy between curves with the same endpoints, \(\Gamma (b,s)=\gamma _c(b)\) for all \(s\), and so \(\p {s}\Gamma (b,s)=0\). Similarly \(\p {s}\Gamma (a,s)=0\) and so
\begin{equation*}\frac {d}{ds}\oint _{\gamma _s} f = 0\end{equation*}for all \(c<s<d\). Thus by the mean value theorem and 1381Problem 1381, \(\oint _{\gamma _c}f=\oint _{\gamma _d} f\).
Let \(\Omega \subseteq \C \) be an open set, let \(\gamma _c\) and \(\gamma _d\) be two curves homotopic in \(\Omega \) with the same endpoints, and let \(f:\Omega \to \C \) be holomorphic. Show that \(\oint _{\gamma _c} f=\oint _{\gamma _d}f\) even if the homotopy is merely continuous and \(C^1\) in the first variable.
Let \(\Omega \subseteq \C \) be any open set, let \(\gamma _c\) and \(\gamma _d\) be any two closed curves that are homotopic in \(\Omega \), and let \(f:\Omega \to \C \) be holomorphic. Assume the homotopy \(\Gamma \) satisfies the conditions of 1381Problem 1381 and 1382Problem 1382. Show that \(\oint _{\gamma _c} f=\oint _{\gamma _d}f\).
By 1381Problem 1381 and 1382Problem 1382, \(\oint _{\gamma _s} f\) is a continuous function of \(s\) and\begin{align*}\frac {d}{ds}\oint _{\gamma _s} f &= \biggl (f(\Gamma (b,s))\,\p {s}\Gamma (b,s)\biggr ) - \biggl (f(\Gamma (a,s))\,\p {s}\Gamma (a,s)\biggr ) .\end{align*}By definition of homotopy between closed curves, \(\Gamma (b,s)=\Gamma (a,s)\) for all \(s\), and so in particular \(\p {s}\Gamma (b,s)=\p {s}\Gamma (a,s)\). Thus
\begin{align*}\frac {d}{ds}\oint _{\gamma _s} f &= \biggl (f(\Gamma (a,s))\,\p {s}\Gamma (a,s)\biggr ) - \biggl (f(\Gamma (a,s))\,\p {s}\Gamma (a,s)\biggr ) =0 .\end{align*}By the mean value theorem, \(\oint _{\gamma _c} f=\oint _{\gamma _d}f\).
Let \(\Omega \) be open and let \(f:\Omega \to \C \) be holomorphic.
Let \(\gamma :[0,1]\to \Omega \) be homotopic in \(\Omega \) to a point (constant function). Show that \(\oint _\gamma f=0\).
[Generalization.] Let \(D(P,r)\subset \C \). Let \(\varphi :\partial D(P,r)\to \C \) be continuous. Let \(k\) be a nonnegative integer. Define \(f:D(P,r)\to \C \) by
Then \(f\) is \(C^1\) and holomorphic in \(D(P,r)\), and
Prove Theorem 3.1.3.
If \(z\in \partial D(P,r)\), is it necessarily true that \(\lim _{w\to z} f(w)=\varphi (z)\)?
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be holomorphic. Then \(f\in C^\infty (\Omega )\). Moreover, if \(\overline D(P,r)\subset \Omega \), then
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be holomorphic. Then \(\frac {\partial ^k f}{\partial z^k}\) is holomorphic in \(\Omega \) for all \(k\in \N \).
Prove Theorem 3.1.1 and Corollary 3.1.2.
Let \(\overline D(P,r)\subset \Omega \). By the Cauchy integral formula, if \(z\in D(P,r)\) then\begin{equation*}f(z)=\frac {1}{2\pi i} \oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}Because \(f\) is holomorphic, it must be continuous, and so we may apply Theorem 3.1.3.
We perform an induction argument. Suppose that \(f\), \(f'=\p [f]{z},\dots ,f^{(k-1)}=\frac {\partial ^{k-1}f}{\partial z^{k-1}}\) exist and are \(C^1\) and holomorphic in \(D(P,r)\), and that \(f^{(k)}=\frac {\partial ^{k}f}{\partial z^{k}}\) exists and satisfies
\begin{equation*}f^{(k)}(z)=\frac {k!}{2\pi i} \oint _{\partial D(P,r)} \frac {f(\zeta )}{(\zeta -z)^{k+1}}\,d\zeta \end{equation*}in \(D(P,r)\). We have shown that this is true for \(k=0\). By Theorem 3.1.3, we have that \(f^{(k)}\) is also \(C^1\) and holomorphic in \(D(P,r)\), and that
\begin{equation*}f^{(k+1)}=\frac {(k+1)!}{2\pi i} \oint _{\partial D(P,r)} \frac {f(\zeta )}{(\zeta -z)^{k+2}}\,d\zeta .\end{equation*}Because \(f^{(k)}\) is holomorphic, \(f^{(k+1)}=\frac {\partial ^{k+1}f}{\partial z^{k+1}}\). Thus by induction this must be true for all nonnegative integers \(k\).
This proves Corollary 3.1.2 and part of Theorem 3.1.1. To prove that \(f\in C^\infty (\Omega )\), observe that
\begin{equation*}\frac {\partial ^{j+\ell } f}{\partial x^j\partial y^\ell } = \biggl (\p {z}+\p {\bar z}\biggr )^j \biggl (\p {z}-\p {\bar z}\biggr )^\ell f \end{equation*}We can write all partial derivatives of \(f\) (in terms of \(x\) and \(y\)) as linear combinations of \(\frac {\partial ^j f}{\partial z^j}\) and \(\frac {\partial ^{m+n+\ell } f}{\partial x^m\partial y^n\partial \bar z^\ell }\) for various values of \(j\), \(\ell \), \(m\), and \(n\), and so
Suppose that \(P\in \Omega \subseteq \C \) for some open set \(\Omega \). Suppose that \(f\) is continuous on \(\Omega \) and holomorphic on \(\Omega \setminus \{P\}\). Show that \(f\) is holomorphic on \(\Omega \).
We must show that \(\nabla f(P)\) exists, that \(\nabla f\) is continuous at \(P\), and that \(\p [f]{\bar z}(P)=0\). That is, we only need to work at \(P\). Let \(\Omega \) be an open disc centered at \(P\) and contained in \(\Omega \); by definition of open set \(\Omega \) must exist. Then by Theorem 2.3.3 ( 1230Problem 1230) there is a function \(F:\Omega \to \C \) that is holomorphic in \(\Omega \) such that \(f=\p [F]{z}\) in \(\Omega \) (including at \(P\)). By Theorem 3.1.1 and Corollary 3.1.2 ( 1440Problem 1440), \(f=\p [F]{z}\) is \(C^1\) and holomorphic in \(\Omega \), and in particular at \(P\).
Let \(\Omega \subseteq \C \) be open and connected. Show that \(\Omega \) is path connected and that the paths may be taken to be \(C^1\); that is, if \(z\), \(w\in \Omega \) then there is a \(\gamma :[0,1]\to \Omega \) with \(\gamma \) a \(C^1\) function such that \(\gamma (0)=z\) and \(\gamma (1)=w\).
(Morera’s theorem.) Let \(\Omega \subseteq \C \) be open and connected. Let \(f\in C(\Omega )\) be such that \(\oint _\gamma f=0\) for all closed curves \(\gamma \). Then \(f\) is holomorphic in \(\Omega \).
Prove Morera’s theorem. Furthermore, show that there is a function \(F\) holomorphic in \(\Omega \) such that \(F'=f\).
Fix some \(z_0\in \Omega \). Suppose that \(z\in \Omega \). By 1460Memory 1460, there is a \(C^1\) curve \(\psi =\psi _z:[0,1]\to \Omega \) such that \(\psi (0)=z_0\) and \(\psi (1)=z\).Suppose that \(\tau \) is another such curve, that is, a \(C^1\) function \(\tau :[0,1]\to \Omega \) such that \(\tau (0)=z_0\) and \(\tau (1)=z\). Let \(\tau _{-1}(t)=\tau (1-t)\). Then by 1010Problem 1010, we have that \(\oint _{\tau _{-1}} f=-\oint _{\tau } f\). Furthermore, by 1050Problem 1050, there is a \(C^1\) curve \(\gamma :[0,1]\to \C \) such that \(\gamma (0)=\psi (0)=z_0\), \(\gamma (1)=\tau _{-1}(1)=\tau (0)=z_0\) and such that
\begin{equation*}\oint _\gamma f=\oint _\psi f+\oint _{\tau _{-1}}f=\oint _\psi f-\oint _\tau f.\end{equation*}But \(\gamma \) is closed and so \(\oint _\gamma f=0\), and so \(\oint _\psi f=\oint _\tau f\).
Thus, if we define \(F(z)=\oint _{\psi _z} f\), then \(F\) is well defined, as \(F(z)\) is independent of our choice of path \(\psi _z\) from \(z_0\) to \(z\).
Now, let \(z\in \Omega \) and let \(r>0\) be such that \(D(z,r)\subseteq \Omega \); such an \(r\) must exist by definition of \(\Omega \). If \(w\in D(z,r)\setminus \{z\}\), then
\begin{equation*}F(w)-F(z)=\oint _{\psi _w} f-\oint _{\psi _z} f.\end{equation*}Let \(\varphi (t)=z+t(w-z)\), so \(\varphi :[0,1]\to D(z,r)\) is a \(C^1\) path from \(z\) to \(w\). We may assume without loss of generality that \(\psi _w\) is generated from \(\psi _z\) and \(\varphi \) by 1050Problem 1050; thus,
\begin{equation*}\frac {F(w)-F(z)}{w-z}=\frac {1}{w-z}\oint _{\varphi } f =\int _0^1 f(z+t(w-z))\,dt .\end{equation*}A straightforward \(\varepsilon \)-\(\delta \) argument yields that
\begin{equation*}\lim _{w\to z}\frac {F(w)-F(z)}{w-z}=f(z)\end{equation*}so \(F\) possesses a complex derivative at \(z\). Furthermore, \(F'=f\) is continuous on \(\Omega \). Thus \(F\in C^1(\Omega )\) and is holomorphic on \(\Omega \) by 1130Problem 1130, and so by Theorem 3.1.1 and Corollary 3.1.2 \(f=F'\) is \(C^\infty \) (in particular \(C^1\)) and holomorphic in \(\Omega \).
Can you rewrite Morera’s theorem to involve a statement true for all holomorphic functions (can you write it with the phrase “if and only if”)?
State the Root Test and Ratio Test from undergraduate real analysis.
Let \(f\in C^\infty (a,b)\) and let \(a<c<b\). The Taylor series for \(f\) at \(c\) is \(\sum _{n=0}^\infty \frac {f^{(n)}(c)}{n!}(x-c)^n\) (with the convention \(0^0=1\)).
Let \(P_{m,c}(x)=\sum _{n=0}^m \frac {f^{(n)}(c)}{n!}(x-c)^n\) be the \(m\)th partial sum of the Taylor series at \(c\). Suppose that \(x\in (a,b)\), \(x\neq c\), \(m\in \N \). Then there is a \(y_{m}\in (a,b)\) with either \(c<y_m<x\) or \(x<y_m<c\) such that
The Taylor series for \(\sin \), \(\cos \), and \(\exp \) converge to the parent function on all of \(\R \).
Give an example of a function \(f\in C^\infty (\R )\) such that the Taylor series for \(f\) converges for all \(x\in \R \) but such that \(f(x)\neq \sum _{n=0}^\infty \frac {f^{(n)}(c)}{n!}(x-c)^n\) for all \(x\neq c\).
The function\begin{equation*}f(x)=\begin {cases} \exp (-1/x^2),&x\neq 0,\\0, &x=0\end {cases}\end{equation*}satisfies \(f^{(n)}(0)=0\) for all nonnegative integers \(n\), and thus the Taylor series is zero everywhere; however, \(f(x)\neq 0\) if \(x\neq 0\) and so the Taylor series never converges to the function.
Give an example of a function \(f\in C^\infty (0,\infty )\) such that the Taylor series for \(f\) at \(2\) diverges for all \(|x-2|>2\). Can we do this for a function \(f\in C^\infty (\R )\)?
Give an example of a function \(f\in C^\infty (\R )\) such that the Taylor series for \(f\) at \(0\) diverges for all \(x\neq 0\).
Let \(\sum _{n=0}^\infty a_n\) be a series of real numbers. If \(\sum _{n=0}^\infty |a_n|\) converges, then we say \(\sum _{n=0}^\infty a_n\) converges absolutely.
Let \(E\) be a set, let \((X,d)\) be a metric space, and let \(f_k\), \(f:E\to X\). We say that \(f_k\to f\) uniformly on \(E\) if for every \(\varepsilon >0\) there is a \(N\in \N \) such that if \(k\geq N\), then \(d(f_k(z),f(z))<\varepsilon \) for all \(z\in E\).
Let \(E\) be a set, let \((X,d)\) be a metric space, and let \(f_k:E\to X\). We say that \(\{f_k\}_{k=1}^\infty \) is uniformly Cauchy on \(E\) if for every \(\varepsilon >0\) there is a \(N\in \N \) such that if \(n>m\geq N\), then \(d(f_n(z),f-m(z))<\varepsilon \) for all \(z\in E\).
If \(E\) is a set, \(V\) is a vector space, and \(f_k:E\to V\) for each \(k\in \N \), then the series \(\sum _{k=1}^\infty f_k\) converges uniformly to \(f:E\to V\) or is uniformly Cauchy, respectively, if the sequences of partial sums \(\bigl \{\sum _{k=1}^n f_k\bigr \}_{n=1}^\infty \) converge uniformly or are uniformly Cauchy.
Suppose that \((X,d)\) is a complete metric space. Then any uniformly Cauchy sequence is uniformly convergent.
Suppose that \((E,\rho )\) and \((X,d)\) are two metric spaces. Let \(f_k\), \(f:E\to X\). Suppose \(f_k\to f\) uniformly on \(E\) and that each \(f_k\) is continuous. Then \(f\) is also continuous.
Give an example of a compact metric space \((X,d)\) and a sequence of continuous functions from \(X\) to \(\R \) that converge pointwise, but not uniformly, to a continuous function.
Let \(f_k\), \(f:[a,b]\to \R \). Suppose that each \(f_k\) is Riemann integrable and that \(f_k\to f\) uniformly on \([a,b]\). Then \(f\) is Riemann integrable, \(\lim _{k\to \infty }\int _a^b f_k\) exists, and \(\lim _{k\to \infty }\int _a^b f_k=\int _a^b f\).
(The Weierstrauß \(M\)-test.) Suppose that \(A\) is a set and that for each \(n\), \(f_n:A\to \C \) is a bounded function. Suppose that there is a sequence \(\{M_n\}_{n=0}^\infty \subset [0,\infty )\) such that \(|f_n(x)|\leq M_n\) for all \(x\in A\) and \(\sum _{n=0}^\infty M_n<\infty \). Then the series \(\sum _{n=0}^\infty f_n(x)\) converges absolutely and uniformly on \(A\).
Let \(\sum _{n=0}^\infty a_n\) be a series of complex numbers. Show that if \(\sum _{n=0}^\infty |a_n|\) converges then \(\sum _{n=0}^\infty a_n\) converges (that is, that in the complex numbers, we still have that absolute convergence implies convergence).
Let \(a_n=x_n+iy_n\) where \(x_n\), \(y_n\in \R \). Then \(|x_n|\leq |a_n|\) and \(|y_n|\leq |a_n|\). We recall from real analysis that a nondecreasing sequence converges if and only if it is bounded. Therefore \(\{\sum _{n=0}^m |a_n|\}_{m\in \N }\) is bounded. Because \(|x_n|\leq |a_n|\), we have that \(\sum _{n=0}^m |x_n|\leq \sum _{n=0}^m|a_n|\leq \sup _{m\in \N } \sum _{n=0}^m |a_n|\) and so \(\{\sum _{n=0}^m |x_n|\}_{m\in \N }\) is bounded. Thus \(\sum _{n=0}^\infty x_n\) converges absolutely, and therefore \(\sum _{n=0}^\infty x_n\) converges. Similarly, \(\sum _{n=0}^\infty y_n\) converges. By 220Problem 220, \(\sum _{n=0}^\infty a_n\) converges.
(Complex power series.) A complex power series is a formal sum \(\sum _{k=0}^\infty a_k (z-P)^k\) for some \(\{a_k\}_{k=1}^\infty \subseteq \C \). The series converges at \(z\) if \(\lim _{n\to \infty } \sum _{k=0}^n a_k (z-P)^k\) exists.
Suppose that the series \(\sum _{k=0}^\infty a_k (z-P)^k\) converges at \(z=w\) for some \(w\in \C \). Then the series converges absolutely at \(z\) for all \(z\) with \(|z-P|<|w-P|\).
Suppose that the series \(\sum _{k=0}^\infty a_k (z-P)^k\) converges at \(z=w\) for some \(w\in \C \). If \(0<r<|w-P|\), then the series converges uniformly on \(\overline D(P,r)\).
Prove Proposition 3.2.9.
Because \(\sum _{k=0} a_k(w-P)^k\) converges, we have that \(\lim _{k\to \infty } a_k(w-P)^k=0\). In particular, \(\{a_k(w-P)^k\}_{k=0}^\infty \) is bounded. Let \(A=\sup _{k\geq 0} |a_k(w-P)^k|\).Because \(0<r/|w-P|<1\), the geometric series \(\sum _{k=0}^\infty A(r/|w-P|)^k\) converges. Thus for every \(\varepsilon >0\) there is an \(N>0\) such that \(\sum _{k=N}^\infty A(r/|w-P|)^k<\varepsilon \).
If \(z\in \overline D(P,r)\), then \(|z-P|\leq r\) and so \(|a_k(z-P)^k| \leq |a_k(w-P)^k | (r/|w-P|)^k\leq A(r/|w-P|)^k\). We then have that \(\sum _{k=N}^\infty |a_k(z-P)^k|\leq \sum _{k=N}^\infty A(r/|w-P|)^k<\varepsilon \) for all \(z\in \overline D(P,r)\). Furthermore, by Lemma 3.2.3 and 1600Problem 1600 \(\sum _{k=0}^\infty a_k(z-P)^k\) exists, and if \(m\geq N\) then
\begin{align*}\Bigl |\sum _{k=0}^\infty a_k(z-P)^k-\sum _{k=0}^m a_k(z-P)^k\Bigr | &=\Bigl |\sum _{k=m+1}^\infty a_k(z-P)^k\Bigr | \leq \sum _{k=m+1}^\infty |a_k(z-P)^k| <\varepsilon .\end{align*}Thus the series converges uniformly on \(\overline D(P,r)\).
Suppose that the series diverges at \(w\) for some \(w\in \C \). Show that the series diverges at \(z\) for all \(z\) with \(|z-P|>|w-P|\).
Suppose for the sake of contradiction that the series converges at \(z\). By Lemma 3.2.3 with \(z\) and \(w\) interchanged, we know that the series converges at \(w\). But we assumed that the series diverged at \(w\), a contradiction. Therefore the series must diverge at \(z\).
(Radius of convergence.) The radius of convergence of \(\sum _{k=0}^\infty a_k (z-P)^k\) is \(\sup \{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k\) converges\(\}\).
Show that the radius of convergence is also \(\inf \{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k\) diverges\(\}\).
Let \(R_1=\sup \{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k\) converges\(\}\), \(R_2=\inf \{|\zeta -P|:\sum _{k=0}^\infty a_k (\zeta -P)^k\) diverges\(\}\).If \(r\in \{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k\) converges\(\}\), then \(r=|w-P|\) for some \(w\) such that the series converges. If the series diverges at \(\zeta \), then \(|\zeta -P|\geq |w-P|\) by Lemma 3.2.3, and so \(r\) is a lower bound on \(\{|\zeta -P|:\sum _{k=0}^\infty a_k (\zeta -P)^k\) diverges\(\}\). Thus \(r\leq R_2\). So \(R_2\) is an upper bound on \(\{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k\) converges\(\}\), and so \(R_2\geq R_1\).
If \(R_2>R_1\), let \(z\in \C \) be such that \(R_1<|z-P|<R_2\). Then the series either converges or diverges at \(z\). If it converges, then \(|z-P|\in \{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k\) converges\(\}\), and so \(|z-P|\leq R_1\), a contradiction. We similarly derive a contradiction if the series diverges at \(z\), and so we must have that \(R_2=R_1\), as desired.
The root test for real numbers states that if \(\{b_n\}_{n=0}^\infty \subset \R \), then
What does the root test tell us about complex power series?
The root test for real numbers states that if \(\{b_n\}_{n=0}^\infty \subset \R \), then
- If \(\limsup _{n\to \infty } \sqrt [n]{|b_n|} <1\), then \(\sum _{n=0}^\infty b_n\) converges absolutely.
- If \(\limsup _{n\to \infty } \sqrt [n]{|b_n|}>1\), then the sequence \(\{b_n\}_{n=0}^\infty \) is unbounded (and in particular the series \(\sum _{n=0}^\infty b_n\) diverges).
Let \(\sum _{k=0}^\infty a_k(z-P)^k\) be a complex power series. Fix a \(z\in \C \) and observe that
\begin{equation*}\limsup _{k\to \infty }\sqrt [k]{|a_k(z-P)^k|} =|z-P|\limsup _{k\to \infty }\sqrt [k]{|a_k|}.\end{equation*}Thus the series \(\sum _{k=0}^\infty a_k(z-P)^k\) converges if \(|z-P|\limsup _{k\to \infty }\sqrt [k]{|a_k|}<1\) and diverges if \(|z-P|\limsup _{k\to \infty }\sqrt [k]{|a_k|}>1\). Thus the radius of convergence must be
\begin{equation*}\frac {1}{\limsup _{k\to \infty }\sqrt [k]{|a_k|}}\end{equation*}with the convention that \(\frac {1}{0}=\infty \) and \(\frac {1}{\infty }=0\); that is, if \(\limsup _{k\to \infty }\sqrt [k]{|a_k|}=0\) then the series converges everywhere and if \(\limsup _{k\to \infty }\sqrt [k]{|a_k|}=\infty \) then the series diverges unless \(z=P\).
State the ratio test from undergraduate real analysis. What does the ratio test say about power series?
The ratio test for real numbers states that if \(\{b_n\}_{n=0}^\infty \subset \R \), then
- If \(\lim _{n\to \infty } \frac {|b_{n+1}|}{|b_n|}\) exists and is less than \(1\), then \(\sum _{n=0}^\infty b_n\) converges absolutely.
- If \(\lim _{n\to \infty } \frac {|b_{n+1}|}{|b_n|}\) exists and is greater than \(1\), then the sequence \(\{b_n\}_{n=0}^\infty \) is unbounded (and in particular the series \(\sum _{n=0}^\infty b_n\) diverges).
Let \(\sum _{k=0}^\infty a_k(z-P)^k\) be a complex power series. Fix a \(z\in \C \setminus \{P\}\) and observe that if either \(\lim _{k\to \infty } \frac {|a_{k+1}(z-P)^{k+1}|}{|a_k(z-P)^k|}\) or \(\lim _{k\to \infty }\frac {|a_{k+1}|}{|a_k|}\) exists, then the other must exist and
\begin{equation*}\lim _{k\to \infty } \frac {|a_{k+1}(z-P)^{k+1}|}{|a_k(z-P)^k|} = |z-P|\lim _{k\to \infty }\frac {|a_{k+1}|}{|a_k|}.\end{equation*}Thus, the series converges absolutely if \(|z-P|<\lim _{k\to \infty }\frac {|a_k|}{|a_{k+1}|}\) and diverges if \(|z-P|>\lim _{k\to \infty }\frac {|a_k|}{|a_{k+1}|}\), so the radius of convergence must be \(\lim _{k\to \infty }\frac {|a_k|}{|a_{k+1}|}\).
Let \(\sum _{k=0}^\infty a_k (z-P)^k\) be a power series with radius of convergence \(R>0\). Define \(f:D(P,R)\to \C \) by \(f(z)=\sum _{k=0}^\infty a_k (z-P)^k\).
Then \(f\) is \(C^\infty \) and holomorphic in \(D(P,R)\), and if \(n\in \N \) then the series
has radius of convergence at least \(R\) and converges to \(f^{(n)}(z)=\frac {\partial ^n f}{\partial z^n}\).
Begin the proof of Lemma 3.2.10 by showing that \(f\) is continuous on \(D(P,R)\).
If \(m\in \N \), define \(f_m(z)=\sum _{k=0}^m a_k(z-P)^k\). Then each \(f_m\) is continuous. By Proposition 3.2.9, if \(0<r<R\) then \(f_m\to f\) uniformly on \(\overline D(P,r)\).By 1560Memory 1560, we have that \(f\) must be continuous on \(\overline D(P,r)\). But if \(z\in D(P,R)\), then \(|z-P|<R\) and so there is a \(\varepsilon >0\) and an \(r<R\) such that \(D(z,\varepsilon )\subset \overline D(P,r)\), and so \(f\) is continuous at \(z\) for all \(z\in D(P,R)\). Thus \(f\) is continuous on \(D(P,R)\).
Continue the proof of Lemma 3.2.10 by showing that \(f\) is holomorphic in \(D(P,R)\). You may either follow the proof given in the book, use Morera’s theorem, or use another method of proof of your choice (I find Morera’s theorem to be the simplest method of proof).
Complete the proof of Lemma 3.2.10 by showing that
indeed converges to \(f^{(n)}(z)\). Hint: Use Theorem 3.1.1 and 1580Memory 1580.
Let \(P\in \Omega \subseteq \C \) where \(\Omega \) is open, and let \(f\) be holomorphic in \(\Omega \). By Theorem 3.1.1, \(f^{(n)}\) exists everywhere in \(\Omega \). The Taylor series for \(f\) at \(P\) is the power series \(\sum _{k=0}^\infty \frac {f^{(k)}(P)}{k!}(z-P)^k\).
Suppose that the two power series \(\sum _{k=0}^\infty a_k (z-P)^k\) and \(\sum _{k=0}^\infty b_k (z-P)^k\) both have positive radius of convergence and that there is some \(r>0\) such that \(\sum _{k=0}^\infty a_k (z-P)^k=\sum _{n=0}^\infty b_k (z-P)^k\) (and both sums converge) whenever \(|z-P|<r\). Then \(a_k=b_k\) for all \(k\).
Let \(f\) be as in Lemma 3.2.10. Show that the Taylor series for \(f\) at \(P\) is simply \(\sum _{k=0}^\infty a_k (z-P)^k\).
Prove Proposition 3.2.11.
We will solve the previous two problems using a single calculation. Let \(f(z)=\sum _{k=0}^\infty a_k(z-P)^k\) in \(D(P,r)\). Then by Lemma 3.2.10, we must have that \(f\) is holomorphic in \(D(P,r)\), and if \(n\geq 0\) is an integer then\begin{equation*}\frac {f^{(n)}(P)}{n!} =\sum _{k=n}^\infty \frac {k!}{n!(k-n)!} a_k (P-P)^{k-n} .\end{equation*}Recall that in power series we define \(0^0=1\). If \(k>n\) then \((P-P)^{k-n}=0\), and so we have that
\begin{equation*}\frac {f^{(n)}(P)}{n!} =\sum _{k=n}^n \frac {k!}{n!(k-n)!} a_k (P-P)^{k-n} =a_n .\end{equation*}Thus the Taylor series for \(f\) at \(P\) by definition is
\begin{equation*}\sum _{n=0}^\infty \frac {f^{(n)}(P)}{n!} (z-P)^n = \sum _{n=0}^\infty a_n (z-P)^n.\end{equation*}This completes Problem 1700Problem 1700.
Furthermore, if \(a_n\) and \(b_n\) are as in Proposition 3.2.11 and \(f(z)=\sum _{k=0}^\infty a_k(z-P)^k=\sum _{k=0}^\infty b_k(z-P)^k\) in \(D(P,r)\) for some \(r>0\), then \(a_n=\frac {f^{(n)}(P)}{n!}=b_n\) and so \(a_n=b_n\) for all \(n\).
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be a function. If for every \(P\in \Omega \) there is a \(r>0\) with \(D(P,r)\subseteq \Omega \) and a sequence \(\{a_n\}_{n=1}^\infty \subset \C \) such that \(f(z)=\sum _{n=0}^\infty a_n (z-P)^n\) for all \(z\in D(P,r)\), we say that \(f\) is analytic.
Show that analytic functions are holomorphic.
Recall that if \(x\in \R \), then \(\exp x=\sum _{n=0}^\infty \frac {x^n}{n!}\), \(\sin x=\sum _{n=0}^\infty \frac {(-1)^n}{(2n+1)!}x^{2n+1}\), \(\cos x=\sum _{n=0}^\infty \frac {(-1)^n}{(2n)!}x^{2n}\). Show that the functions \(\mathop {\widetilde {\mathrm {exp}}} z=\sum _{n=0}^\infty \frac {z^n}{n!}\), \(\sin z=\sum _{n=0}^\infty \frac {(-1)^n}{(2n+1)!}z^{2n+1}\), and \(\cos z=\sum _{n=0}^\infty \frac {(-1)^n}{(2n)!}z^{2n}\) are holomorphic on \(\C \) and take the correct values at all real numbers.
(We will show in Section 3.3 that \(\mathop {\widetilde {\mathrm {exp}}} (z)=\exp (z)\), where \(\exp (z)\) is as defined in Section 1.2.)
Let \(\Omega \subseteq \C \) be an open set and let \(f\) be holomorphic in \(\Omega \). Let \(D(P,r)\subseteq \Omega \) for some \(r>0\).
Then the Taylor series for \(f\) at \(P\) has radius of convergence at least \(r\) and converges to \(f(z)\) for all \(z\in D(P,r)\).
Let \(f\) be holomorphic in \(D(P,r)\) and let \(0<\varrho <r\). Begin the proof of Theorem 3.3.1 by showing that there is a power series with radius of convergence at least \(\varrho \) that converges to \(f\) in \(D(P,\varrho )\).
Without loss of generality we may assume \(P=0\). By the Cauchy integral formula (Theorem 2.4.2), if \(z\in D(0,r)=D(P,r)\) and \(|z|<\varrho <r\), then\begin{equation*}f(z)=\oint _{\partial D(0,\varrho )} \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}We must take \(\varrho <r\) to ensure that \(f\) is continuous up to \(\partial D(0,\varrho )\).
Because \(|z|<|\zeta |\) all \(\zeta \in \partial D(0,\varrho )\), we have that
\begin{equation*}\frac {1}{\zeta -z}=\frac {1/\zeta }{1-z/\zeta } =\sum _{k=0}^\infty \frac {z^k}{\zeta ^{k+1}}.\end{equation*}Thus
\begin{equation*}f(z)=\oint _{\partial D(0,\varrho )}\sum _{k=0}^\infty \frac {f(\zeta )}{\zeta ^{k+1}}z^k\,d\zeta .\end{equation*}Because \(f\) is continuous on the compact set \(\partial D(0,\varrho )\), it is bounded there. Let \(m=\sup _{\partial D(0,\varrho )}|f|\). Then \(|\frac {f(\zeta )}{\zeta ^{k+1}}z^k|\leq m|z|^k/\varrho ^{k+1}\). But \(\sum _{k=0}^\infty m|z|^k/\varrho ^{k+1}\) is a convergent geometric series, so by the Weierstrauß \(M\)-test we have that the series converges uniformly on \(\partial D(0,r)\). Thus by 1580Memory 1580 we may interchange the sum with the integral and see that
\begin{equation*}f(z)=\sum _{k=0}^\infty z^k\oint _{\partial D(0,\varrho )} \frac {f(\zeta )}{\zeta ^{k+1}}\,d\zeta \end{equation*}and the sum converges.
Let \(a_k(\varrho )=\oint _{\partial D(0,\varrho )} \frac {f(\zeta )}{\zeta ^{k+1}}\,d\zeta \) for any \(\varrho \in (0,r)\); we have shown that \(\sum _{k=0}^\infty a_k(\varrho )\, z^k\) converges in \(D(0,\varrho )\) to \(f(z)\). But by Proposition 3.2.11 we have that \(a_k(\varrho )\) is independent of \(\varrho \), and so we must have that \(\sum _{k=0}^\infty a_k(\varrho )\, z^k\) converges in \(D(0,r)\) to \(f(z)\), as desired.
Complete the proof of Theorem 3.3.1 by showing that the power series for \(f\) in \(D(P,r)\) must be the Taylor series for \(f\) at \(P\) and that the radius of convergence of the Taylor series for \(f\) at \(P\) must be at least \(R\).
By the previous problem, we know that if \(P\in \Omega \) then there are complex numbers \(a_k\) such that \(\sum _{k=0}^\infty a_k(z-P)^k\) has radius of convergence at least \(r\) and \(f(z)=\sum _{k=0}^\infty a_k(z-P)^k\) for all \(z\in D(P,r)\).But by 1700Problem 1700, we have that the Taylor series for \(f\) is simply \(\sum _{k=0}^\infty a_k(z-P)^k\), and by assumption \(\sum _{k=0}^\infty a_k(z-P)^k\) converges to \(f\) in \(D(P,r)\), and so the Taylor series converges to \(f\) in \(D(P,r)\).
Let \(f\) be holomorphic in \(D(P,r)\). Let \(R\) be the radius of convergence of the Taylor series for \(f\) at \(P\). Observe that \(R\geq r\). Suppose \(R>r\). Show that there is a unique function \(F\) that is holomorphic in \(D(P,R)\) with \(F=f\) in \(D(P,r)\).
Define \(F:D(P,R)\to \C \) by \(F(z)=\sum _{k=0}^\infty \frac {f^{(k)}(P)}{k!}(z-P)^k\). By assumption the power series does converge in \(D(P,R)\), and by Lemma 3.2.10 \(F\) is holomorphic in \(D(P,R)\).Suppose for the sake of contradiction that \(G\) is holomorphic in \(D(P,R)\) and that \(G=f=F\) in \(D(P,r)\). A straightforward induction argument shows that if \(n\in \N \) then \(G^{(n)}=f^{(n)}=F^{(n)}\) in \(D(P,r)\), and so in particular \(G^{(n)}(P)=F^{(n)}(P)\). But by Theorem 3.3.1 we have that
\begin{equation*}F(z)=\sum _{n=0}^\infty \frac {F^{(n)}(P)}{n!}(z-P)^n, \qquad G(z)=\sum _{n=0}^\infty \frac {G^{(n)}(P)}{n!}(z-P)^n\end{equation*}for all \(z\in D(P,R)\), and so we must have that \(G=F\) in \(D(P,R)\).
Let \(f\) be an analytic function in a neighborhood of \(P\). Show that the Taylor series for \(f'\) at \(P\) has the same radius of convergence as the Taylor series for \(f\) at \(P\).
Let \(r\) be the radius of convergence of the Taylor series for \(f\) at \(P\). By Lemma 3.2.10 we have that\begin{equation*}f'(z)=\sum _{k=0}^\infty \frac {f^{(k+1)}(P)}{k!}z^k\end{equation*}in \(D(P,r)\), and in particular that the series has radius of convergence at least \(r\).
Suppose that the power series for \(f'\) at \(P\) has radius of convergence \(R\); by the above we have that \(R\geq r\). Then
\begin{equation*}g(z)=\sum _{k=0}^\infty \frac {f^{(k+1)}(P)}{k!}z^k\end{equation*}is holomorphic in \(D(P,R)\) and equals \(f'\) in \(D(P,r)\). By 840Problem 840 there is a holomorphich function \(G:D(P,R)\to \C \) such that \(G'=g\) in \(D(P,R)\). By adding a constant, we may require that \(G(P)=f(P)\).
By Theorem 3.3.1 we have that the Taylor series for \(G\) at \(P\) has radius of convergence at least \(R\) and converges to \(G\) in \(D(P,R)\).
But the Taylor series for \(G\) is
\begin{equation*}\sum _{n=0}^\infty \frac {G^{(n)}(P)}{n!} (z-P)^n = G(P)+\sum _{n=1}^\infty \frac {g^{(n-1)}(P)}{n!} (z-P)^n = f(P)+\sum _{n=1}^\infty \frac {f^{(n)}(P)}{n!} (z-P)^n \end{equation*}because \(G'=g\) in \(D(P,R)\) and so \(G^{(n)}=g^{(n-1)}\), \(G(P)=f(P)\), and \(g=f'\) in \(D(P,r)\) and so \(g^{(k)}(P)=(f')^{(k)}(P)=f^{(k+1)}(P)\). This is the Taylor series for \(f\), and so we must have that the Taylor series for \(f\) has radius of convergence at least \(R\) as well. Thus \(R\geq r\) and \(r\geq R\), so \(r=R\), as desired.
Let \(\Omega =\{re^{i\theta }:0<r<\infty ,\>-\pi <\theta <\pi \}=\C \setminus (-\infty ,0]\). Define \(F:\Omega \to \C \) by \(F(re^{i\theta })=\ln r+i\theta \) whenever \(-\pi <\theta <\pi \). Recall that \(F\) is holomorphic and that \(F'(z)=\frac {1}{z}\) for all \(z\in \Omega \).
Recall from Proposition 1.4.3 that if \(f\) is holomorphic in \(\Omega \) then \(\p [f]{z}=\p [f]{x}\) in \(\Omega \). By Corollary 3.1.2 ( 1440Problem 1440), \(\p [f]{z}=\p [f]{x}\) is holomorphic in \(\Omega \). A straightforward induction argument yields that \(\frac {\partial ^n f}{\partial z^n}=\frac {\partial ^n f}{\partial x^n}\) in \(\Omega \) for all \(n\in \N \).
Show that the functions \(\mathop {\widetilde {\mathrm {exp}}}\), \(\sin \), and \(\cos \) in 1730Problem 1730 are the only functions that are holomorphic on all of \(\C \) and take the correct values for all real numbers. In particular, show that \(\mathop {\widetilde {\mathrm {exp}}} (z)=\exp (z)\) for all \(z\in \C \).
Let \(g:\R \to \R \) be infinitely differentiable and suppose that there exists a function \(f\) that is holomorphic on all of \(\C \) and satisfies \(f(x)=g(x)\) for all \(x\in \R \).Note that \(g'(x)\) denotes the real derivative \(\lim _{\substack {y\to x\\y\in \R }}\frac {g(y)-g(x)}{y-x}\), while \(f'(z)\) denotes the complex derivative \(\lim _{\substack {w\to z\\w\in \C }}\frac {f(w)-f(z)}{w-z}\).
We then have that \(\frac {\partial ^n }{\partial x^n}f(x)=\frac {d^n}{dx^n} g(x)=g^{(n)}(x)\) for all \(x\in \R \). By the previous fact, \(\frac {\partial ^n }{\partial z^n}f(z)\big \vert _{z=x}=\frac {d^n}{dx^n}g(x)\) for all \(x\in \R \). By Theorem 2.2.1 and Theorem 2.2.2, we have that
\begin{equation*}f^{(n)}(x)=\frac {\partial ^n }{\partial z^n}f(z)\bigg \vert _{z=x}=\frac {d^n}{dx^n}g(x)\end{equation*}for all \(x\in \R \). By Theorem 3.3.1, we must have that
\begin{equation*}f(z)=\sum _{n=0}^\infty \frac {f^{(n)}(0)}{n!} z^n=\sum _{n=0}^\infty \frac {g^{(n)}(0)}{n!} z^n\end{equation*}for all \(z\in \C \). In particular, for a given \(g\) there is at most one function \(f\) that satisfies the given conditions, and so the functions given in 1730Problem 1730 by power series are the unique functions that satisfy these conditions with \(g(x)=\exp x\), \(g(x)=\cos x\) or \(g(x)=\sin x\).
In particular, by 651Problem 651, \(\exp z\) is holomorphic in \(\C \) and satisfies \(\exp x= \mathop {\widetilde {\mathrm {exp}}} x=e^x\) for all \(x\in \R \), and so \(\exp z=\mathop {\widetilde {\mathrm {exp}}} z\) for all \(z\in \C \).
Suppose that \(\sum _{n=0}^\infty a_n z^n\) and \(\sum _{n=0}^\infty b_n z^n\) are two power series with radius of convergence at least \(r\). Show that
has radius of convergence at least \(r\) and that
for all \(|z|<r\).
Let \(f(z)=\sum _{n=0}^\infty a_n z^n\) and let \(g(z)=\sum _{n=0}^\infty b_n z^n\); by 1680Problem 1680, \(f\) and \(g\) are both holomorphic in \(D(0,r)\). Thus \(h=fg\) is holomorphic in \(D(0,r)\). By 1740Problem 1740 and 1750Problem 1750, we must have that\begin{equation*}\sum _{n=0}^\infty \frac {h^{(n)}(0)}{n!} z^n\end{equation*}has radius of convergence at least \(r\) and must converge to \(h(z)=f(z)g(z)\). A straightforward induction argument and the Leibniz rule ( 570Fact 570) shows that
\begin{equation*}h^{(n)}(z)=\sum _{k=0}^n\frac {n!}{k!(n-k)!} f^{(k)}(z)\, g^{(n-k)}(z) \end{equation*}and so by Lemma 3.2.10 we have that
\begin{equation*}\frac {h^{(n)}(0)}{n!}=\sum _{k=0}^n a_k\,b_{n-k}.\end{equation*}
(The Cauchy estimates) Let \(f:\Omega \to \C \) be holomorphic and let \(\overline D(P,r)\subseteq \Omega \). Let \(k\in \N _0\). Then
Prove Theorem 3.4.1.
Let \(\gamma :[0,2\pi ]\to \C \) be given by \(\gamma (t)=e^{it}\), so \(\gamma \) is a parameterization of \(\partial D(P,r)\). By Theorem 3.1.1,\begin{equation*}f^{(k)}(P)=\frac {k!}{2\pi i}\oint _\gamma \frac {f(\zeta )}{(\zeta -P)^{k+1}}d\zeta .\end{equation*}By 980Problem 980,
\begin{equation*}\biggl |\oint _\gamma \frac {f(\zeta )}{(\zeta -P)^{k+1}}d\zeta \biggr | \leq \ell (\gamma ) \sup _{\zeta \in \widetilde \gamma } \frac {|f(\zeta )|}{|\zeta -P|^{k+1}}\end{equation*}where \(\ell (\gamma )=\int _0^{2\pi }|\gamma '(t)|\,dt=2\pi r\). But \(\widetilde \gamma =\partial D(P,r)\), and so if \(\zeta \in \widetilde \gamma \) then \(|\zeta -P|=r\). Thus this reduces to
\begin{equation*}|f^{(k)}(P)|\leq \frac {k!}{2\pi } 2\pi r \sup _{\zeta \in \widetilde \gamma } \frac {|f(\zeta )|}{r^{k+1}} =\frac {k!}{r^k} \sup _{\zeta \in \widetilde \gamma } |f(\zeta )| \end{equation*}as desired.
Let \(k\), \(n\in \N \). Show that there is a function \(f\in C^\infty (\R )\) with \(\sup _{x\in \R } |f(x)|\leq 1\) but with \(|f^{(k)}(0)|\geq n\).
If \(f\) is holomorphic on a connected open set \(\Omega \) and \(\p [f]{z}=0\) in \(\Omega \), then \(f\) is constant. (This was proven in 610Problem 610.)
A function \(f:\C \to \C \) is entire if \(f\) is holomorphic on all of \(\C \).
[Liouville’s theorem.] A bounded entire function is constant.
Prove Liouville’s theorem.
Let \(f:\C \to \C \) be entire and let \(M\in \R \) be such that \(|f(z)|\leq M\) for all \(z\in \C \). By assumption \(M\) exists.By the Cauchy estimates (Theorem 3.4.1),
\begin{equation*}|f'(z)|\leq \frac {M}{r}\end{equation*}for all \(r>0\). Taking the limit as \(r\to \infty \) yields that \(f'(z)=0\) for all \(z\) and the result follows from Lemma 3.4.2.
Let \(P\in \C \), \(r>0\), \(k\in \N \), and let \(f:D(P,r)\to \C \) be holomorphic. Suppose that \(\frac {\partial ^{k+1} f}{\partial z^{k+1}}=0\) in \(D(P,r)\). Show that \(f\) is a polynomial of degree at most \(k\).
By Theorem 3.3.1, we have that\begin{equation*}f(z)=\sum _{n=0}^\infty \frac {f^{(n)}(P)}{n!}(z-P)^n.\end{equation*}But \(f^{(k+1)}\equiv 0\) in \(D(P,r)\), and therefore all derivatives of order higher than \(k\) are zero. We then have that
\begin{equation*}f(z)=\sum _{n=0}^k \frac {f^{(n)}(P)}{n!}(z-P)^n\end{equation*}which is a polynomial of degree at most \(k\).
Show that this is still true in an arbitrary connected open set.
If \(f\) is entire and there is a constant \(C\in \R \) and a \(k\in \N _0\) such that \(|f(z)|\leq C+C|z|^k\) for all \(z\in \C \), then \(f\) is a polynomial of degree at most \(k\).
(The fundamental theorem of algebra.) Let \(p\) be a nonconstant (holomorphic) polynomial. Prove that \(p\) has a root; that is, prove that there is an \(\alpha \in \C \) with \(p(\alpha )=0\).
Let \(p(z)=a_0+a_1z+\dots +a_nz^n\) be a polynomial. Show that there is an \(R\in (0,\infty )\) such that if \(|z|\geq R\), then \(|p(z)|\geq |a_n|\,|z|^n/2\).
Prove the fundamental theorem of algebra.
(Corollary 3.4.6.) Let \(p\) be a polynomial of degree \(k>0\). Can \(p\) necessarily be factored completely?
Yes. Clearly every linear polynomial (\(k=1\)) can be factored completely.Suppose that all polynomials of degree at most \(k\) can be factored completely. Let \(p\) be a polynomial of degree \(k+1\).
By the Fundamental Theorem of Algebra, there is a root \(r_1\in \C \) such that \(p(r_1)=0\). By the standard division algorithm, this means that there is a polynomial \(q\) of degree \(k\) such that \(p(z)=(z-r_1)q(z)\). By our induction hypothesis \(q\) may be factored completely, and so \(p\) may be factored completely.
A domain is a connected open subset of \(\C \).
Let \(\Omega \subseteq \C \) be a domain. Let \(f_n\), \(f:\Omega \to \C \). Suppose that each \(f_n\) is holomorphic in \(\Omega \) and that if \(K\subset \Omega \) is compact, then \(f_n\to f\) uniformly on \(K\). Then \(f\) is holomorphic in \(\Omega \).
Use Theorem 3.1.3 and Theorem 2.4.2 to prove Theorem 3.5.1.
Suppose that \(P\in \C \), \(r>0\), and \(\overline D(P,r)\subset \Omega \). Then by the Cauchy integral formula,\begin{equation*}f_n(z)=\frac {1}{2\pi i} \oint _{\partial D(P,r)} \frac {f_n(\zeta )}{\zeta -z}\,d\zeta \end{equation*}for all \(z\in D(P,r)\) and all \(n\).
But \(\partial D(P,r)\subset \Omega \) is compact, and so by assumption \(f_n\to f\) uniformly on \(\partial D(P,r)\). For any fixed \(z\in D(P,r)\), \(\frac {1}{\zeta -z}\) is bounded on \(\partial D(P,r)\), and so \(\frac {f_j(\zeta )}{\zeta -z}\to \frac {f(\zeta )}{\zeta -z}\) uniformly on \(\partial D(P,r)\). By assumption, if \(z\in D(P,r)\) then \(f_n(z)\to f(z)\), while by 1580Memory 1580
\begin{equation*}\lim _{n\to \infty }\oint _{\partial D(P,r)} \frac {f_n(\zeta )}{\zeta -z}\,d\zeta =\oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta . \end{equation*}In particular,
\begin{equation*}f(z)=\frac {1}{2\pi i} \oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta \end{equation*}Because each \(f_n\) is continuous on \(\Omega \) and \(f_n\to f\) uniformly on \(\partial D(P,r)\), we have that \(f\) is continuous on \(\partial D(P,r)\). By Theorem 3.1.3, this implies that \(f\) is holomorphic in \(D(P,r)\), as desired.
Prove Theorem 3.5.1 using Morera’s theorem.
Give an example of a sequence of functions in \(C^\infty (\R )\) that converge uniformly to a function that is not differentiable.
Let \(f_j(x)=\frac {x}{\sqrt {x^2+1/j^2}}\). \(f_j\) is infinitely differentiable on \(\R \), but \(\{f_j\}_{j=1}^\infty \) converges uniformly to \(|x|\).
Let \(\Omega \subseteq \C \) be a domain. Let \(f_n\), \(f:\Omega \to \C \). Suppose that each \(f_n\) is holomorphic in \(\Omega \) and that if \(K\subset \Omega \) is compact, then \(f_n\to f\) uniformly on \(K\). Then \(\frac {\partial }{\partial z} f_n\to \frac {\partial }{\partial z} f\) on \(\Omega \) and the convergence is uniform on all compact subsets \(X\) of \(\Omega \).
Prove Corollary 3.5.2.
Let \(X\subset \Omega \) be compact. Because \(\Omega \) is open, a standard real analysis argument yields that there is a \(r>0\) and finitely many points \(z_1\), \(z_2,\dots z_N\) such that \(X\subset \cup _{n=1}^N D(z_n,r/3)\).Let \(K=\cup _{n=1}^N \overline D(z_n, 2r/3)\). Then \(K\) is the union of finitely many compact sets, and so is compact. Furthermore, if \(z\in X\) then \(z\in D(z_\ell ,r/3)\) for some \(\ell \) and so \(\overline D(z,r/3)\subset D(z_\ell ,2r/3)\subset K\).
By assumption \(f_n\to f\) uniformly on \(K\). That is, for every \(\varepsilon >0\) there is a \(M\in \N \) such that if \(n\geq M\) then \(|f_n-f|<\varepsilon \) on \(K\).
By Theorem 3.5.1, \(f\) and thus \(f_n-f\) is holomorphic, and so by Theorem 3.4.1 we have that if \(n\geq M\) and \(z\in X\) then
\begin{equation*}|f'(z)-f_n'(z)|\leq \frac {3}{r}\sup _{\partial D(z,r/3)} |f-f_n|\leq \frac {3\varepsilon }{r}.\end{equation*}Thus \(f_n'\to f'\) uniformly on \(X\), as desired.
Give an example of a sequence of functions \(\{f_n\}_{n=1}^\infty \) in \(C^\infty (\R )\) that converge uniformly to a differentiable function \(f\) but where \(f_n'\) does not converge to \(f'\).
Let \(f_n(x)=\frac {1}{n}\sin (n^2x)\). Then \(f_n\to 0\) uniformly but \(f_n'(x)=n\cos (n^2x)\) does not converge to zero.
Show that the real Taylor series for \(f(x)=\ln x\) at any point \(c\in (0,\infty )\) has a positive radius of convergence and converges to \(\ln x\).
If \(k\geq 1\), then \(\ln ^{(k)}(x)=(-1)^{k-1} (k-1)! x^{-k}\). So the Taylor series for \(\ln \) expanded about \(c\) is\begin{equation*}\ln (c)+\sum _{k=1}^\infty \frac {(-1)^{k-1} }{kc^k} (x-c)^k.\end{equation*}By either the ratio or root test, we have that the series converges whenever \(|x-c|<c\).
It remains to show that the series in fact converges to the function \(\ln x\). We have that \(f(x)=\ln x\) is infinitely differentiable on \((0,\infty )\). Suppose that \(m\geq 2\) is an integer.
Recall from 1500Memory 1500 that if \(x>c\) then
\begin{align*}\ln x &= \ln (c)+\sum _{k=1}^{m-1}\frac {(-1)^{k-1} }{kc^k} (x-c)^k + \frac {(-1)^{m-1}}{m (y_m)^{m} } (x-c)^m\end{align*}for some \(y_m\) with \(c<y_m<x\). If \(0<x<c\) then we will use a different form of the Taylor remainder, namely
\begin{align*}\ln x&= \ln (c)+\sum _{k=1}^{m-1}\frac {(-1)^{k-1} }{kc^k} (x-c)^k + \frac {(-1)^{m-1}}{m (y_m)^{m} } (x-y_m)^{m-1}(x-c)\end{align*}for some \(y_m\) with \(x<y_m<c\).
In the first case, \(0<x-c<c<y_m\) and so \(|\frac {x-c}{y_m}|^m\leq 1\) for all \(m\). (Recall that \(y_m\) may depend on \(m\) and so we cannot take a limit as \(m\to \infty \)!) In the second case, \(0<y_m-x<y_m-0=y_m\) and so \(|\frac {(x-y_m)^{m-1}}{(y_m)^{m-1}}|\leq 1\). Thus we have either that
\begin{equation*}\Bigl |\ln x-\ln c-\sum _{k=1}^{m-1}\frac {(-1)^{k-1} }{kc^k} (x-c)^k\Bigr | \leq \frac {1}{m}\end{equation*}or
\begin{equation*}\Bigl |\ln x-\ln c-\sum _{k=1}^{m-1}\frac {(-1)^{k-1} }{kc^k} (x-c)^k\Bigr | \leq \frac {c-x}{mx}.\end{equation*}In either case the right hand side converges to zero as \(m\to \infty \) and so we must have that the infinite series converges to \(\ln x\), as desired.
Let \((X,d)\) be a metric space and let \(Y\subseteq X\). Then \((Y,d)\) is also a metric space. If \(F\subseteq Y\) is closed in \((Y,d)\), then we say that \(F\) is relatively closed. If \(G\subseteq Y\) is open in \((Y,d)\), then we say that \(G\) is relatively open.
Suppose that \(F\subseteq X\) is closed. Then \(F\cap Y\) is relatively closed in \(Y\). In particular, if \(F\subseteq Y\) and \(F\) is closed in \((X,d)\), then \(F\) is relatively closed in \((Y,d)\).
Suppose that \(G\subseteq X\) is open. Then \(G\cap Y\) is relatively open in \(Y\).
Give an example of a metric space \((X,d)\), a subset \(Y\subset X\), and a set \(F\subseteq Y\) such that \(F\) is relatively closed in \((Y,d)\) but not closed in \((X,d)\).
Give an example of a metric space \((X,d)\), a subset \(Y\subset X\), and a set \(G\subseteq Y\) such that \(G\) is relatively open in \((Y,d)\) but not open in \((X,d)\).
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic. Suppose that there is a \(P\in \Omega \) and an \(r>0\) such that \(D(P,r)\subseteq \Omega \) and \(f=0\) in \(D(P,r)\). Then \(f=0\) everywhere in \(\Omega \).
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic. Suppose that there is a \(P\in \Omega \) such that \(f^{(k)}(P)=0\) for all \(k\in \N _0\) (that is, all integers \(k\) such that \(k\geq 0\)). Then \(f=0\) everywhere in \(\Omega \).
In this problem we begin the proof of Corollaries 3.6.2 and 3.6.5. Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be holomorphic. Let
Show that \(E=F\).
If \(\zeta \in E\), let \(r>0\) be such that \(D(\zeta ,r)\subseteq \Omega \) and \(f=0\) in \(D(\zeta ,r)\). Then all first partial derivatives of \(f\) are zero in \(D(\zeta ,r)\); by induction, all derivatives of \(f\) (of any order) are zero in \(D(\zeta ,r)\), and in particular at \(\zeta \). Thus \(\zeta \in F\) and so \(E\subseteq F\).Conversely, suppose that \(\zeta \in F\), so \(\zeta \in \Omega \) and \(\frac {\partial ^k f}{\partial z^k}(\zeta )=0\) for all \(k\in \N _0\). Because \(\Omega \) is open there is an \(r>0\) such that \(D(\zeta ,r)\subset \Omega \). By Theorem 3.3.1, if \(z\in D(\zeta ,r)\) then
\begin{equation*}f(z)=\sum _{k=0}^\infty \frac {f^{(k)}{\zeta }}{k!}(z-\zeta )^k.\end{equation*}But because \(f^{(k)}{\zeta }=0\) for all \(k\), we have that \(f(z)=0\) for all \(z\in D(\zeta ,r)\), as desired.
\(E\) is clearly open. Complete the proof of Corollaries 3.6.2 and 3.6.5 by showing that \(F\) is relatively closed in \(\Omega \) and then drawing appropriate conclusions if \(\Omega \) is connected.
Let \(\{z_n\}_{n=1}^\infty \subseteq F\subseteq \Omega \) and suppose that \(z_n\to z\) for some \(z\in \Omega \).If \(k\in \N _0\), then \(f^{(k)}(z_n)=0\) for all \(n\) because \(z_n\in F\). But each \(f^{(k)}\) is continuous on \(\Omega \) by Theorem 3.1.1, and so we must have that \(f^{(k)}(z)=0\) because \(z_n\to z\) and \(f^{(k)}(z_n)\to 0\). Thus \(z\in F\).
We have showed that \(E\) is open in \(\C \) (and therefore relatively open in \(\Omega \)) and equals \(F\), which relatively closed in \(\Omega \). By definition of connected set, we must have that either \(E=F=\Omega \) or \(E=F=\emptyset \). Recalling the definitions of \(E\) and \(F\) completes the proof of both corollaries.
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic.
Suppose that there is a sequence \(\{z_n\}_{n=1}^\infty \) such that
Then \(f(z)=0\) for all \(z\in \Omega \).
Prove Theorem 3.6.1. You may use Corollary 3.6.2.
Let \(r>0\) be such that \(D(z_0,r)\subseteq \Omega \); \(r\) must exist because \(\Omega \) is open. By Theorem 3.3.1, there are constants \(a_k\) such that if \(z\in D(z_0,r)\), then \(\sum _{k=0}^\infty a_k(z-z_0)^k\) converges absolutely to \(f(z)\).We claim that \(a_k=0\) for all \(k\); this immediately implies that \(f=0\) in \(D(z_0,r)\), and so by Corollary 3.6.2 we have that \(f=0\) in \(\Omega \).
We have that, if \(m\geq 0\) is an integer, then \(\sum _{k=m}^\infty a_k(z-z_0)^k\) also converges absolutely. Define \(f_m:D(z_0,r)\to \C \) by
\begin{equation*}f_m(z)=\sum _{k=m}^\infty a_k(z-z_0)^k.\end{equation*}We observe that for any fixed \(z\in D(z_0,r)\), \(\lim _{m\to \infty } f_m(z)=0\).
If \(z=z_0\) then the series \(\sum _{k=m}^\infty a_k(z-z_0)^{k-m}\) converges trivially. If \(z\in D(z_0,r)\setminus \{z_0\}\), then \((z-z_0)^{-m}\) is independent of \(k\), and so if \(\sum _{k=m}^\infty a_k(z-z_0)^k\) converges absolutely then so does
\begin{equation*}\sum _{k=m}^\infty [a_k(z-z_0)^k](z-z_0)^{-m} =\sum _{k=m}^\infty a_k(z-z_0)^{k-m}.\end{equation*}We define \(h_m:D(z_0,r)\to \C \) by \(h_m(z)=\sum _{k=m}^\infty a_k(z-z_0)^{k-m}\). By Lemma 3.2.10, each \(h_m\) is holomorphic and therefore continuous in \(D(z_0,r)\). Furthermore, if \(z\in D(z_0,r)\) then \(\lim _{m\to \infty } h_m(z)=0\).
We have that \(f(z)=f_0(z)=(z-z_0)^0h_0(z)\) for all \(z\in D(z_0,r)\) (with the convention \(0^0=1\) usual in power series).
Suppose that we have established that \(f(z)=f_m(z)=(z-z_0)^m h_m(z)\) for some fixed integer \(m\) and all \(z\in D(z_0,r)\). Then \(a_m=h_m(z_0)=\lim _{n\to \infty } h_m(z_n)\) because \(h_m\) is continuous. But \(h_m(z_n)=f(z_n)/(z_n-z_0)^m=0\) and so \(a_m=0\). Thus \(f(z)=f_m(z)=f_{m+1}(z)=(z-z_0)^{m+1}h_{m+1}(z)\) and \(a_m=0\). By induction we have that \(f(z)=f_m(z)=f_{m+1}(z)=(z-z_0)^{m+1}h_{m+1}(z)\) and \(a_m=0\) for all \(m\in \Z \), and so as noted above the conclusion follows from Corollary 3.6.2.
Give an example of a function \(f\) holomorphic in \(\C \setminus \{0\}\) and a sequence of points \(z_n\in \C \setminus \{0\}\) with \(z_n\to 0\) and with \(f(z_n)=0\) but where \(f(z)\neq 0\) for some \(z\in \C \setminus \{0\}\).
Let \(f(z)=\sin (1/z)\) and let \(z_n=\frac {1}{n\pi }\). Then \(z_n\to 0\) and \(f(z_n)=0\) for all \(n\in \N \), but \(f(z)\neq 0\) for many values of \(z\).
Let \(S\subseteq \C \). Suppose that \(P\in \C \) and that, for every \(r>0\), there is a \(z\in D(P,r)\cap S\) with \(z\neq P\). Then we say that \(P\) is an accumulation point for \(S\).
Rewrite Theorem 3.6.1 in terms of accumulation points rather than sequences and prove your version.
Theorem. Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic. Let \(Z=\{z\in \Omega :f(z)=0\}\). If \(Z\) has an accumulation point that lies in \(\Omega \), then \(f(z)=0\) for all \(z\in \Omega \).
Let \(\Omega \) be a connected open set and let \(f:\Omega \to \C \) be holomorphic and not constant. Let \(P\in \Omega \). Show that there is a \(r>0\) with \(D(P,r)\subseteq \Omega \) and such that \(f\neq 0\) on \(D(P,r)\setminus \{P\}\).
Suppose that \(f\) and \(g\) are holomorphic in a connected open set \(\Omega \). If \(\{z\in \Omega :f(z)=g(z)\}\) has an accumulation point in \(\Omega \), then \(f(z)=g(z)\) for all \(z\in \Omega \).
Prove Corollary 3.6.3.
Let \(h(z)=f(z)-g(z)\). Then \(h\) is holomorphic in \(\Omega \) and \(\{z\in \Omega :f(z)=g(z)\}=\{z\in \Omega :h(z)=0\}\). Thus \(\{z\in \Omega :h(z)=0\}\) has an accumulation point. By 2020Problem 2020, \(h\equiv 0\) in \(\Omega \), and so \(f\equiv g\) in \(\Omega \).
Let \(\Omega \subseteq \C \setminus \{0\}\) be open and connected and contain a positive real. Show that there is at most one holomorphic function \(f:\Omega \to \C \) such that \(f(x)=\ln x\) for all \(x\in (0,\infty )\cap \Omega \).
Suppose that \(f\) and \(g\) are holomorphic in a connected open set \(\Omega \). If \(fg=0\) everywhere in \(\Omega \), then either \(f\equiv 0\) or \(g\equiv 0\) in \(\Omega \).
Prove Corollary 3.6.4.
Suppose \(f\not \equiv 0\). Then there is a \(\zeta \in \Omega \) such that \(f(\zeta )\neq 0\). By continuity, there is a \(r>0\) such that \(f\neq 0\) in \(D(\zeta ,r)\), and so we must have that \(g\equiv 0\) in \(D(\zeta ,r)\). The result follows from Corollary 3.6.2.
Let \(f\) be holomorphic in the connected open set \(\Omega \) and let \(K\subseteq \Omega \) be compact. Show that if \(f\) has infinitely many zeroes in \(K\) then \(f\equiv 0\) in \(\Omega \).
A Laurent series is a formal expression of the form \(\sum _{k=-\infty }^\infty a_k(z-P)^k\), where \(P\in \C \) and each \(a_k\in \C \), with the convention that \(0^0=1\) and \(0\cdot 0^k=0\) even if \(k<0\).
We say that the Laurent series \(\sum _{k=-\infty }^\infty a_k(z-P)^k\) converges at \(z\) if the two series \(\sum _{k=0}^\infty a_k(z-P)^k\) and \(\sum _{k=1}^\infty a_{-k}(z-P)^{-k}\) both converge, and write
Suppose that the doubly infinite series \(\sum _{k=-\infty }^\infty a_k(z-P)^k\) converges at \(z=w_1\) and at \(z=w_2\), where \(0<|w_1-P|<|w_2-P|\). Then the series converges absolutely at \(z\) for all \(z\) such that \(|w_1-P|<|z-P|<|w_2-P|\).
Prove Lemma 4.2.1.
Let \(\sum _{k=-\infty }^\infty a_k(z-P)^k\) be a doubly infinite series that converges at \(z=w\) for at least one \(w\in \C \setminus \{P\}\). Then there are extended real numbers \(r\) and \(R\) with \(0\leq r\leq |w-P|\leq R\leq \infty \) such that the series converges absolutely if \(r<|z-P|<R\) and diverges if \(|z-P|<r\) or \(|z-P|>R\).
Furthermore, if \(r<\tau \leq \sigma <R\) then the series converges uniformly on \(\overline D(P,\sigma )\setminus D(P,\tau )\).
Prove the existence of \(r\) and \(R\) in Lemma 4.2.2.
Establish the uniform convergence on \(\overline D(P,\sigma )\setminus D(P,\tau )\) in Lemma 4.2.2.
Let \(w_1\) and \(w_2\) satisfy \(r<|w_1-P|<\sigma \) and \(\tau <|w_2-P|<R\). Then \(\sum _{k=-\infty }^\infty a_k(w_1-P)^k\) converges, and so in particular \(\sum _{k=0}^\infty a_k(w_1-P)^k\) converges. By Proposition 3.2.9 we have that \(\sum _{k=0}^\infty a_k(z-P)^k\) converges uniformly on \(\overline D(P,\sigma )\).Similarly, \(\sum _{k=-\infty }^\infty a_k(w_2-P)^k\) converges, and so in particular \(\sum _{k=-\infty }^{-1} a_k(w_2-P)^k\) converges. Thus the power series \(\sum _{n=1}^\infty a_{-n}\bigl (\frac {1}{w_2-P}\bigr )^n\) converges, and so \(\sum _{n=1}^\infty a_{-n}\zeta ^n\) converges uniformly to some \(g(\zeta )\) for \(\zeta \in \overline D(0,\frac {1}{\tau })\). That is, for every \(\varepsilon >0\) there is a \(M>0\) such that if \(m\geq M\) and \(|\zeta |\leq 1/\tau \), then \(|g(\zeta )-\sum _{n=1}^m a_{-n}\zeta ^n|<\varepsilon \). Thus, if \(m\geq M\) and \(|z-P|\geq \tau \), then \(\zeta =\frac {1}{z-P}\) satisfies \(|\zeta |\leq 1/\tau \) and so \(|g(\zeta )-\sum _{k=-m}^{-1} a_{k}(z-P)^k|<\varepsilon \). Thus the series \(\sum _{k=-\infty }^{-1} a_k(z-P)^k\) converges uniformly on \(\{z\in \C :|z-P|\geq \tau \}=\C \setminus D(P,\tau )\).
Thus both series converge uniformly on \(\overline D(P,\sigma )\setminus D(P,\tau )\), and so their sum converges uniformly in this region, as desired.
Let \(f(z)=\sum _{j=-\infty }^\infty a_j(z-P)^j\). Show that \(f\) is holomorphic on \(D(P,R)\setminus \overline D(P,r)\), where \(r\) and \(R\) are as in Lemma 4.2.2.
If \(r=R\) or if the series converges nowhere then there is nothing to prove. Otherwise, let \(f_N(z)=\sum _{j=-N}^N a_j(z-P)^j\). Then each \(f_N\) is holomorphic and \(f_N\to f\) uniformly on all compact subsets of \(D(P,R)\setminus \overline D(P,r)\). By Theorem 3.5.1 \(f\) must also be holomorphic.
Give examples of Laurent series for which:
- One such series is \(\sum _{k=-\infty }^{-1} z^k+\sum _{k=0}^\infty \frac {1}{2^k} z^k\).
- One such series is \(\sum _{k=-\infty }^{-1} \frac {1}{|k|!} z^k+\sum _{k=0}^\infty z^k\).
- One such series is \(\sum _{k=-\infty }^{-1} z^k+\sum _{k=0}^\infty \frac {1}{k!} z^k\).
- One such series is \(\sum _{k=-\infty }^\infty \frac {1}{|k|!}z^k\).
Let \(\sum _{j=-\infty }^\infty a_j(z-P)^j\) and \(\sum _{j=-\infty }^\infty b_j(z-P)^j\) be doubly infinite series that both converge to the same value if \(r<|z-P|<R\), for some \(0\leq r<R\leq \infty \). Then \(a_j=b_j\) for all \(j\).
Let \(\sum _{k=-\infty }^\infty a_k(z-P)^k\) be a doubly infinite series that converges to \(f(z)\) if \(r<|z-P|<R\), for some \(0\leq r<R\leq \infty \). Let \(r<\tau <R\). Compute
for any \(n\in \Z \). Then prove Proposition 4.2.4.
Observe that\begin{align*} \frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -P)^{n+1}}\,d\zeta &= \frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {1}{(\zeta -P)^{n+1}}\sum _{k=-\infty }^\infty a_k (\zeta -P)^k\,d\zeta = \frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \sum _{k=-\infty }^\infty a_k (\zeta -P)^{k-n-1}\,d\zeta \end{align*}by definition of \(f\). By Lemma 4.2.2, the series converges uniformly on the compact set \(\partial D(P,\tau )\). Because \(\frac {1}{(\zeta -P)^{n+1}}\) is bounded on \(\partial D(P,\tau )\), we have that \(\sum _{k=-\infty }^\infty a_k (\zeta -P)^{k-n-1}\) also converges uniformly, and so by 1580Memory 1580 we have that
\begin{align*}\frac {1}{2\pi i} &\oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -P)^{n+1}}\,d\zeta = \sum _{k=-\infty }^\infty a_k \frac {1}{2\pi i} \oint _{\partial D(P,\tau )} (\zeta -P)^{k-n-1}\,d\zeta .\end{align*}Using the parameterization \(\gamma (t)=P+\tau e^{it}\), \(0\leq t\leq 2\pi \), of \(\partial D(P,\tau )\), we compute
\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} (\zeta -P)^{k-n-1}\,d\zeta =\frac {\tau ^{k-n} }{2\pi }\int _0^{2\pi } e^{it(k-n)} \,dt \end{equation*}which equals one if \(k=n\) and equals zero otherwise, so
\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -P)^{n+1}}\,d\zeta = a_n.\end{equation*}Similarly, we have that
\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -P)^{n+1}}\,d\zeta =b_n\end{equation*}and so \(b_n=a_n\) for all \(n\).
If \(z\in \C \), then we take \(D(z,0)=\emptyset \), \(\overline D(z,0)=\{z\}\) (this is not the metric space closure of \(D(z,0)\)), and \(D(z,\infty )=\overline D(z,\infty )=\C \).
Let \(0\leq r<R\leq \infty \) and let \(\Omega =D(P,R)\setminus \overline D(P,r)\) for some \(P\in \C \).
Suppose that \(f:\Omega \to \C \) is holomorphic. Then there exist constants \(a_k\) such that the series
converges absolutely to \(f(z)\) for all \(z\in \Omega \).
Furthermore, if \(r<\sigma <\tau <R\) then the series converges uniformly on \(\overline D(P,\tau )\setminus D(P,\sigma )\).
Let \(f\), \(r\), \(R\) be as in Theorem 4.3.2. If \(r<\sigma <|z-P|<\tau <R\), then
Let \(f\), \(r\), \(R\), \(\sigma \), \(\tau \), and \(z\) be as in Theorem 4.3.1. We will use Theorem 4.3.1 to prove Theorem 4.3.2 (so you may not use Theorem 4.3.2). Begin the proof of Theorem 4.3.1 by computing
Because \(z\) is outside \(D(P,\sigma )\), we have that \(\oint _{\partial D(P,\sigma )} \frac {1}{\zeta -z}\,d\zeta =0\) by Theorem 2.4.3. Because \(z\in D(P,\tau )\), we have that \(\oint _{\partial D(P,\tau )} \frac {1}{\zeta -z}\,d\zeta =2\pi i\) by the special case of the Cauchy integral formula (Lemma 2.4.1). Thus\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(0,\tau )} \frac {f(z)}{\zeta -z} \,d\zeta - \frac {1}{2\pi i} \oint _{\partial D(0,\sigma )} \frac {f(z)}{\zeta -z} \,d\zeta =f(z).\end{equation*}
Let \(r<\sigma <|z-P|<\tau <R\). Complete the proof of Theorem 4.3.1 by computing
Define\begin{equation*}g(\zeta )=\begin {cases}\frac {f(\zeta )-f(z)}{\zeta -z}, &\zeta \neq z,\\f'(z),&\zeta =z.\end {cases}\end{equation*}Clearly \(g\) is holomorphic in \(\Omega \setminus \{z\}\). Furthermore, \(\lim _{\zeta \to z} g(\zeta )=g(z)\) and so \(g\) is continuous at \(z\). By Theorem 2.3.3 and Corollary 3.1.2, we have that \(g\) is holomorphic in \(\Omega \).
Thus by Proposition 2.6.6 we have that
\begin{equation*}\oint _{\partial D(P,\sigma )} g=\oint _{\partial D(P,\tau )} g\end{equation*}and so by definition of \(g\) we have that
\begin{equation*} \oint _{\partial D(P,\tau )} \frac {f(\zeta )-f(z)}{\zeta -z} \,d\zeta = \oint _{\partial D(P,\sigma )} \frac {f(\zeta )-f(z)}{\zeta -z} \,d\zeta .\end{equation*}Straighforward algebra completes the proof.
Let \(f\), \(r\), \(R\) be as in Theorem 4.3.2. We seek to show that \(f\) may be represented by a Laurent series. By 2120Problem 2120, the only possible Laurent series is \(\sum _{k=-\infty }^\infty a_k(z-P)^k\), where
for any \(\tau \in (r,R)\). (By Proposition 2.6.6 we have that \(a_k\) does not depend on \(\tau \).) Begin the proof of Theorem 4.3.2 by showing that the sum \(\sum _{k=-\infty }^\infty a_k(z-P)^k\) converges absolutely for all \(z\in \Omega \). (By 2090Problem 2090, this means that the series converges uniformly on compact subsets of \(\Omega \).) Hint: Let \(r<\sigma <|z-P|<\tau <R\) and find upper bounds on \(a_k\) in terms of \(M_\tau =\sup _{\partial D(P,\tau )}|f|\) and \(M_\sigma =\sup _{\partial D(P,\sigma )}|f|\).
Continue the proof of Theorem 4.3.2 by showing that, if \(r<\sigma <|z-P|<\tau <R\), then
Define\begin{equation*}g(z)=\sum _{k=0}^\infty a_k(z-P)^k,\qquad h(z)=\frac {1}{2\pi i}\oint _{\partial D(P,\tau )} \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}By the previous problem and Lemma 3.2.10, \(g\) is holomorphic in \(D(P,\tau )\), while by Theorem 3.1.3 and because holomorphic functions are continuous, we have that \(h\) is also holomorphic in \(D(P,\tau )\).
Furthermore, by our generalization of Theorem 3.1.3, we have that if \(n\geq 0\) is an integer then
\begin{equation*}h^{(n)}(z)=\frac {n!}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -z)^{n+1}}\,d\zeta \end{equation*}while by Lemma 3.2.10
\begin{equation*}g^{(n)}(z)=\sum _{k=n}^\infty \frac {k!}{(k-n)!}a_k(z-P)^{k-n}.\end{equation*}In particular,
\begin{equation*}h^{(n)}(P)=\frac {n!}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -P)^{n+1}}\,d\zeta , \quad g^{(n)}(z)=n! a_n.\end{equation*}By definition of \(a_n\), we have that \(g^{(n)}(P)-h^{(n)}(P)=0\) for all \(n\geq 0\), and so by Corollary 3.6.5, \(g=h\) everywhere in \(D(P,\tau )\).
Complete the proof of Theorem 4.3.2.
We need only show that if \(r<\sigma <|z-P|<\tau <R\), then\begin{equation*}\sum _{k=-\infty }^{-1} a_k(z-P)^k = -\frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}Recall that
\begin{equation*}a_k=\frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \frac {f(\zeta )}{(\zeta -P)^{k+1}}\,d\zeta .\end{equation*}Then
\begin{equation*}\sum _{k=-\infty }^{-1} a_k (z-P)^k =\sum _{k=-\infty }^{-1} \frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \frac {f(\zeta )\,(z-P)^k}{(\zeta -P)^{k+1}}\,d\zeta .\end{equation*}Let \(M=\sup _{|\zeta -P|=\sigma } |f(\zeta )|\); because \(f\) is continuous on \(\Omega \) and \(\partial D(P,\sigma )\subset \Omega \) is compact, \(M\) is finite. Then
\begin{equation*}\left |\frac {f(\zeta )}{(\zeta -P)^{k+1}}(z-P)^k\right |\leq M\sigma ^{-1}\left (\frac {|z-P|}{\sigma }\right )^k\end{equation*}for all \(\zeta \in \partial D(P,\sigma )\), and \(\sum _{k=-\infty }^{-1} M\sigma ^{-1}\left (\frac {|z-P|}{\sigma }\right )^k\) converges because \(|z-P|>\sigma \). Thus by 1590Memory 1590 we have that
\begin{equation*}\sum _{k=-\infty }^{-1} \frac {f(\zeta )}{(\zeta -P)^{k+1}}\ (z-P)^k\end{equation*}converges absolutely for all \(\zeta \in \partial D(P,\sigma )\), uniformly for \(\zeta \in \partial D(P,\sigma )\). Thus by 1580Memory 1580, we have that
\begin{equation*}\sum _{k=-\infty }^{-1} a_k (z-P)^k =\frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \sum _{k=-\infty }^{-1} \frac {f(\zeta )\,(z-P)^k}{(\zeta -P)^{k+1}} \,d\zeta .\end{equation*}Applying the formula for the sum of a geometric series, we see that
\begin{align*} \sum _{k=-\infty }^{-1} a_k (z-P)^k &= \frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} f(\zeta )\frac {1}{z-P} \sum _{k=-\infty }^{-1} \biggl (\frac {z-P}{\zeta -P}\biggr )^{k+1} \,d\zeta \\&= \frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} f(\zeta )\frac {1}{z-P} \sum _{n=0}^{\infty } \biggl (\frac {\zeta -P}{z-P}\biggr )^{n} \,d\zeta \\&= \frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} f(\zeta )\frac {1}{z-P} \frac {1}{1-(\zeta -P)/(z-P)} \,d\zeta \\&= \frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \frac {f(\zeta )}{z-\zeta } \,d\zeta \end{align*}as desired.
If \(\Omega \subseteq \C \) is open and \(P\in \C \), and if \(f\) is a function defined and holomorphic in \(\Omega \setminus \{P\}\), then we say that \(f\) has an isolated singularity at \(P\).
If \(f\) has an isolated singularity at \(P\) and if \(f\) is defined and bounded on \(D(P,r)\setminus \{P\}\) for some \(r>0\), then we say that \(f\) has a removable singularity at \(P\).
[The Riemann removable singularities theorem.] Suppose that \(f\) has a removable singularity at \(P\). Then \(\lim _{z\to P}f(z)\) exists (and is a finite complex number), and the function
is holomorphic on \(\Omega \).
(Observe that if the limit exists, then \(\widehat f\) is continuous on \(\Omega \) and holomorphic on \(\Omega \setminus \{P\}\), so the fact that \(\widehat f\) is holomorphic is simply 1450Problem 1450.)
Suppose that \(P\in \Omega \subseteq \C \) for some open set \(\Omega \). Suppose that \(f:\Omega \setminus \{P\}\to \C \) is holomorphic and that \(\lim _{z\to P} (z-P)f(z)=0\). Then \(\lim _{z\to P}f(z)\) exists.
- (a)
- Let \(f(x,y)=\sin (1/(x^2+y^2))\). Then \(f\) is bounded and is \(C^\infty \) on \(\R ^2\setminus \{(0,0)\}\) but has no limits at the origin.
- (b)
- Let \(f(x)=\sgn (x)\) (that is, \(f(x)=1\) if \(x>1\) and \(f(x)=0\) if \(x<0\)). Then \(f\) is bounded and \(f'=0\) is bounded but \(\lim _{x\to 0} f(x)\) does not exist.
If \(f\) has an isolated singularity at \(P\), and if \(\lim _{z\to P}|f(z)|=\infty \), then we say that \(f\) has a pole at \(P\).
For part (a), let \(z\in \Psi \). Then \(f(z)\neq 0\). By 2030Problem 2030 there is a \(r>0\) with \(D(z,r)\subseteq \Omega \) and such that \(f\neq 0\) on \(D(z,r)\setminus \{z\}\). Thus \(f\neq 0\) on \(D(z,r)\) and so \(D(z,r)\subseteq \Psi \). Thus \(\Psi \) is open.For part (b), observe that \(\Omega \setminus \{P\}\) is open and \(f\) is holomorphic on \(\Omega \setminus \{P\}\). Thus \(\Psi =\{z\in \Omega \setminus \{P\}:f(z)\neq 0\}\) is open. Because \(W=\Psi \cup \{P\}\), we need only consider the point \(P\).
Because \(\Omega \) is open we have that there is a \(\varrho >0\) such that \(D(P,\varrho )\subseteq \Omega \). By definition of limit there is a \(\delta >0\) such that, if \(0<|z-P|<\delta \), then \(|f(z)|>7\) and so in particular \(f(z)\neq 0\). Let \(r=\min (\delta ,\varrho )\); then \(P\in W\) by definiton and, if \(z\in D(P,r)\) with \(z\neq P\), then \(z\in \Omega \) and \(f(z)\neq 0\), and so \(z\in W\). Thus \(D(P,r)\subseteq W\) and so \(W=\Psi \cup D(P,r)\) is the union of two open sets, and so is open.
Suppose that \(\Omega \) is an open set and that \(g:\Omega \to \C \) is holomorphic. Then \(f(z)=1/g(z)\) is holomorphic on \(\Psi \), where \(\Psi =\Omega \setminus \{z\in \Omega :g(z)=0\}\), and if \(P\) is an isolated zero of \(f\) then \(\lim _{z\to P} |f(z)|=\infty \).
Suppose that \(P\in \Omega \subseteq \C \) for some open set \(\Omega \). Suppose that \(f:\Omega \setminus \{P\}\to \C \) is holomorphic and that \(\lim _{z\to P} |f(z)|=\infty \). Let \(g:W\setminus \{P\}\to \C \) be given by \(g(z)=1/f(z)\). Then \(g\) has a removable singularity at \(P\) and \(\lim _{z\to P} g(z)=0\).
If \(f\) has an isolated singularity at \(P\), and if \(f\) has neither a pole nor a removable singularity at \(P\), then we say that \(f\) has an essential singularity at \(P\).
State the precise \(N\)-\(\delta \) negation of the statement “\(\lim _{z\to P} |f(z)|=\infty \)”.
If it is false that \(\lim _{z\to P} |f(z)|=\infty \) (either the limit does not exists, or it exists but is finite), then there exists a \(N\in \R \) such that for every \(\delta >0\) there is a \(z\) with \(0<|z-P|<\delta \) and such that \(|f(z)|\leq N\).
Let \(f:\C \setminus \{0\}\to \C \) be given by \(f(z)=\exp (1/z)\). Let \(w\in \C \) with \(w\neq 0\) and let \(r>0\). Show that \(w=f(z)\) for some \(z\in D(0,r)\setminus \{0\}\).
Recall that there exist real numbers \(\rho \) and \(\theta \) such that \(w=\rho e^{i\theta }\). Furthermore \(\rho >0\) and we may require \(0\leq \theta <2\pi \).Define \(z_k\) by \(1/z_k=\ln \rho +i\theta +2k\pi i\). Then \(f(z_k)=w\) for all \(k\in \Z \). But \(\lim _{k\to \infty }|1/z_k|=\infty \), and so we may find a \(k\) such that \(|z_k|<r\).
Show that if \(r>0\) then \(\sup _{0<|z|<r} |\exp (1/z)|=\infty \) and \(\inf _{0<|z|<r} |\exp (1/z)|=0\). Conclude that \(\lim _{z\to 0}|\exp (1/z)|\) does not exist (even in the sense of infinite limits).
Because \(|\exp (1/z)|>0\) for all \(z\in \C \), we have that \(\inf _{0<|z|<r} |\exp (1/z)|\geq 0\).Observe that
\begin{equation*}\lim _{\substack {x\to 0^-\\x\in \R }} \exp (1/x)=0\end{equation*}and
\begin{equation*}\lim _{\substack {x\to 0^+\\x\in \R }} \exp (1/x)=\infty .\end{equation*}Thus, for every \(r>0\) and every \(N>0\), there are numbers \(x^-\), \(x^+\in \R \) with \(-r<x^-<0\), \(0<x^+<r\) and with \(\exp (1/x^-)<1/N\), \(\exp (1/x^+)>N\). Thus
\begin{equation*}\sup \{|\exp (1/z)|:0<|z|<r\}\geq |\exp (1/x^+)|>N\end{equation*}and
\begin{equation*}0<\inf \{|\exp (1/z)|:0<|z|<r\}\leq |\exp (1/x^1)|<1/N.\end{equation*}Because \(N\) was arbitrary, taking the limit as \(N\to \infty \) completes the proof that \(\sup _{0<|z|<r} |\exp (1/z)|=\infty \) and \(\inf _{0<|z|<r} |\exp (1/z)|=0\).
Recall the definitions of \(\limsup \) and \(\liminf \):
\begin{gather*} \limsup _{z\to 0} |\exp (1/z)|=\lim _{r\to 0^+}\sup _{0<|z|<r} |\exp (1/z)|, \quad \liminf _{z\to 0} |\exp (1/z)|=\lim _{r\to 0^+}\inf _{0<|z|<r} |\exp (1/z)|.\end{gather*}Thus
\begin{equation*}\limsup _{z\to 0} |\exp (1/z)|=\infty \neq 0=\liminf _{z\to 0} |\exp (1/z)|.\end{equation*}Recall that if \(\phi \) is real-valued and \(\lim _{z\to P} \phi (z)\) exists (even in the infinite sense), then \(\limsup _{z\to P} \phi (z)=\lim _{z\to P} \phi (z)=\liminf _{z\to P} \phi (z)\). Therefore \(\lim _{z\to 0} |\exp (1/z)|\) cannot exist, even in the infinite sense, for if it did exist then we would necessarily have that \(\limsup _{z\to 0} |\exp (1/z)|=\lim _{z\to 0} |\exp (1/z)|=\liminf _{z\to 0} |\exp (1/z)|\) which cannot be true.
Suppose that \(f\) has an essential singularity at \(P\). Let \(r>0\) be such that \(D(P,r)\subseteq \Omega \). Then \(f(D(P,r)\setminus \{P\})\) is dense in \(\C \).
Prove Theorem 4.1.4.
We will prove the contrapositive. Suppose that \(f:\Omega \setminus \{P\}\to \C \) has an isolated singularity at \(P\) and that \(f(D(P,r)\setminus \{P\})\) is not dense in \(\C \). We will show that \(f\) does not have an essential singularity at \(P\).Because \(f\) is not dense, there exists some \(\lambda \in \C \) and some \(\varepsilon >0\) such that \(D(\lambda ,\varepsilon )\cap f(D(P,r)\setminus \{P\})=\emptyset \). Let \(g:D(P,r)\setminus \{P\}\to \C \) be given by
\begin{equation*}g(z)=\frac {1}{f(z)-\lambda }.\end{equation*}Because \(f(z)\notin D(\lambda ,\varepsilon )\), we have that \(|g(z)|\leq 1/\varepsilon \) (and in particular exists) for all \(z\in D(P,r)\setminus \{P\}\). Thus \(g\) has a removable singularity at \(P\), and so by Theorem 4.1.1 we have that \(\lim _{z\to P} g(z)\) exists (and is a finite complex number).
If \(\lim _{z\to P} g(z)=0\), then \(\lim _{z\to P} |g(z)|=0\). Thus
\begin{equation*}\lim _{z\to P} |f(z)|=\lim _{z\to P} \biggl |\lambda +\frac {1}{g(z)}\biggr |=\infty \end{equation*}and so \(f\) has a pole at \(P\). Otherwise,
\begin{equation*}\lim _{z\to P} f(z)=\lim _{z\to P} \lambda +\frac {1}{g(z)}=\lambda +\frac {1}{\lim _{z\to P} g(z)}\end{equation*}is a finite complex number. In particular \(f\) is bounded on sufficiently small neighborhoods of \(P\), and so \(f\) has a removable singularity at \(P\). In either case \(f\) does not have an essential singularity. This completes the proof.
Show that if \(f\) has an isolated singularity at \(P\) and \(\limsup _{z\to P}|f(z)|\neq \liminf _{z\to P} |f(z)|\) then \(f\) has an essential singularity at \(P\).
If \(f\) has a pole at \(P\), then \(\lim _{z\to P} |f(z)|=\infty \) and so we must have that both \(\limsup _{z\to P}|f(z)|=\lim _{z\to P} |f(z)|=\infty \) and \(\liminf _{z\to P}|f(z)|=\lim _{z\to P} |f(z)|=\infty \). Thus they are equal.If \(f\) has a removable singularity at \(P\), then by Theorem 4.1.1 \(\lim _{z\to P} f(z)\in \C \). Thus both \(\limsup _{z\to P}|f(z)|=|\lim _{z\to P} f(z)|\) and \(\liminf _{z\to P}|f(z)|=|\lim _{z\to P} f(z)|\). Thus they are equal.
Show that if \(f\) has an essential singularity at \(P\) then \(\limsup _{z\to P}|f(z)|=\infty \) and \(\liminf _{z\to P} |f(z)|=0\).
Let \(\delta >0\) be such that \(f\) is defined on \(D(P,\delta )\setminus \{P\}\); by definition of isolated singularity, this is true whenever \(\delta >0\) is small enough. We claim that \(\sup _{z\in D(P,\delta )\setminus \{P\}}|f(z)|=\infty \) and \(\inf _{z\in D(P,\delta )\setminus \{P\}}|f(z)|=0\). Recalling that\begin{gather*}\limsup _{z\to P} |f(z)|=\lim _{r\to 0^+}\sup _{0<|z-P|<r} |f(z)|, \quad \liminf _{z\to P} |f(z)|=\lim _{r\to 0^+}\inf _{0<|z-P|<r} |f(z)|\end{gather*}this suffices to complete the proof.
But \(f(D(P,\delta )\setminus \{P\})\) is dense in \(\C \). Thus for each \(\varepsilon >0\), there exist points \(\zeta \), \(w\in D(P,\delta )\setminus \{P\}\) such that \(f(\zeta )\in D(0,\varepsilon )\) and \(f(w)\in \C \setminus \overline {D}(0,1/\varepsilon )\). Thus
\begin{equation*}\sup _{z\in D(P,\delta )\setminus \{P\}}|f(z)| \geq |f(w)|>1/\varepsilon , \quad \inf _{z\in D(P,\delta )\setminus \{P\}}|f(z)| \leq |f(\zeta )|<\varepsilon \end{equation*}for all \(\varepsilon >0\); thus \(\sup _{z\in D(P,\delta )\setminus \{P\}}|f(z)|=\infty \) and, because \(|f(z)|\geq 0\) and so \(0\leq \inf _{z\in D(P,\delta )\setminus \{P\}}|f(z)|\), we must have that \(\inf _{z\in D(P,\delta )\setminus \{P\}}|f(z)|=0\).
Give an example of a \(C^\infty \) function \(f:\R \setminus \{0\}\to \R \) such that \(\limsup _{x\to 0} |f(x)|=\infty \) and \(\liminf _{x\to 0} |f(x)|=0\) but such that \(f(x)\geq 0\) for all \(x\in \R \).
An example of such a function is \(f(x)=\frac {1}{x^2}(1+\sin (1/x))\).
Suppose that \(f\) is holomorphic in the punctured disc \(\Omega =D(P,R)\setminus \{P\}\) for some \(P\in \C \) and some \(0<R\leq \infty \). Then \(f\) has a unique Laurent series
which converges absolutely to \(f(z)\) for all \(z\in D(P,R)\setminus \{P\}\). The convergence is uniform on compact subsets of \(D(P,R)\setminus \{P\}\). The coefficients are given by
for any \(0<\sigma <R\).
Suppose that \(f\) has a removable singularity at \(P\). Show that \(a_k=0\) for all \(k<0\).
By the Riemann removable singularities theorem (Theorem 4.1.1) there is a function \(\widehat f\) holomorphic in \(D(P,R)\) with \(\widehat f(z)=f(z)\) for all \(z\in D(P,R)\setminus \{P\}\). Because \(\widehat f\) is holomorphic, there are constants \(b_k\) such that \(\widehat f(z)=\sum _{k=0}^\infty b_k (z-P)^k\) for all \(z\in D(P,R)\). Let
\begin{equation*}c_k=\begin {cases} b_k, &k\geq 0,\\0,&k<0.\end {cases}\end{equation*}Thus \( f(z)=\sum _{k=-\infty }^\infty c_k (z-P)^k\) for all \(z\in D(P,R)\setminus \{P\}\). By uniqueness of Laurent series (Proposition 4.2.4), \(a_k=c_k\) for all \(k\in \Z \) and so \(a_k=0\) for all \(k<0\).
Suppose that \(a_k=0\) for all \(k<0\). Show that \(f\) has a removable singularity at \(P\).
We have that \(f(z)=\sum _{k=0}^\infty a_k(z-P)^k\) for all \(z\in D(P,R)\setminus \{P\}\) and the series converges for all such \(z\). By Lemma 3.2.3, the radius of convergence of the power series is at least \(R\). Thus, by Lemma 3.2.10 the series converges to a function \(\widehat f\) holomorphic in \(D(P,R)\). In particular, \(\widehat f\) is bounded on \(\overline D(P,R/2)\), and so \(f\) must also be bounded on \(D(P,R/2)\).
Suppose that \(f\) is holomorphic in \(D(P,r)\) for some \(r>0\) and \(f(P)=0\). Then \(f(z)=\sum _{k=0}^\infty a_k (z-P)^k\) for all \(z\in D(P,r)\). The order of the zero of \(f\) at \(P\) is the smallest \(n\) such that \(a_n\neq 0\); note that the order is at least \(1\).
Suppose that \(f\) is holomorphic in \(D(P,R)\setminus \{P\}\) and that \(f\) has a pole at \(P\). Then \(1/f\) is holomorphic in \(D(P,r)\setminus \{P\}\) for some \(r>0\), has a removable singularity at \(P\), and the holomorphic extension \(g\) of \(1/f\) to \(D(P,r)\) satisfies \(g(P)=0\). Let \(n\) be the order of the zero of \(g\) at \(P\). Then \((z-P)^n f(z)\) has a removable singularity at \(P\).
Suppose that \(f\) has a pole at \(P\). Show that there is some \(N>0\) such that \(a_{-N}\neq 0\) and such that \(a_k=0\) for all \(k<-N\).
By Proposition 4.3.3, \(f\) has a Laurent series in \(D(P,r)\setminus \{P\}\), so\begin{equation*}f(z)=\sum _{k=-\infty }^\infty a_k(z-P)^k \end{equation*}for all \(z\in D(P,r)\setminus \{P\}\).
Let \(n\) be as in Problem 4.15b. Then
\begin{equation*}(z-P)^nf(z)=\sum _{k=-\infty }^\infty a_k(z-P)^{k+n} =\sum _{\ell =-\infty }^\infty a_{\ell -n}(z-P)^{\ell } \end{equation*}has a removable singularity at \(P\), and so by 2280Problem 2280 we must have that \(a_{\ell -n}=0\) for all \(\ell <0\), that is, \(a_k=0\) for all \(k<-n\).
Conversely, \(f\) does not have a removable singularity at \(P\), and so by the contrapositive to 2290Problem 2290, there is at least one \(m<0\) such that \(a_m\neq 0\). Thus \(\{m\in \Z :a_m\neq 0,\>m<0\}\) is nonempty and bounded below. Letting \(N=\min \{m\in \Z :a_m\neq 0,\>m<0\}\) completes the proof.
Suppose that \(f\) is holomorphic in \(D(P,R)\setminus \{P\}\), that \(f\) is not bounded in \(D(P,R/2)\setminus \{P\}\), and that there is a \(m\in \N \) such that the function \(g\) given by \(g(z)=(z-P)^m f(z)\) is bounded in \(D(P,R/2)\). Then \(f\) has a pole at \(P\).
Suppose that there is some \(N>0\) such that \(a_{-N}\neq 0\) and such that \(a_k=0\) for all \(k<-N\). Show that \(f\) has a pole at \(P\).
We may write\begin{equation*}f(z)=\sum _{k=-N}^\infty a_k(z-P)^k\end{equation*}for all \(z\in D(P,R)\setminus \{P\}\). Because \(a_{-N}\neq 0\), \(f\) does not have a removable singularity, and so \(f\) cannot be bounded in \(D(P,R/2)\setminus \{P\}\).
Then
\begin{equation*}(z-P)^Nf(z)=\sum _{k=-N}^\infty a_k(z-P)^{k+N}=\sum _{\ell =0}a_{\ell -N}(z-P)^\ell \end{equation*}for all \(z\in D(P,R)\setminus \{P\}\) and the series converges in that region. Thus the power series \(\sum _{k=-N}^\infty a_k(z-P)^{k+N}=\sum _{\ell =0}a_{\ell -N}(z-P)^\ell \) must yield a function holomorphic in \(D(P,R)\), and in particular bounded in the compact set \(\overline D(P,R/2)\). The result follows from Problem 4.15c.
Suppose that \(f\) has a pole at \(P\). Then there is some \(N>0\) such that \(a_{-N}\neq 0\) and such that \(f(z)=\sum _{k=-N}^\infty a_k (z-P)^k\) for all \(z\) in a punctured neighborhood of \(P\) (that is, for all \(z\) in in \(D(P,r)\setminus \{P\}\) for some \(r>0\)). We call \(N\) the order of the pole at \(P\). If \(N=1\) we say that \(f\) has a simple pole at \(P\).
If you write “pole of order 0”, I will assume that you mean “removable singularity”. If you write “zero of order 0 at \(P\)”, I will assume that you mean “holomorphic near \(P\) and nonzero at \(P\).” If you write “zero/pole of order \(-n\)”, for \(n\in \N \), I will assume that you mean a pole/zero of order \(n\) (possibly after the additional step of applying the Riemann removable singularities theorem).
Show that \(f\) has an essential singularity at \(P\) if and only if, for all \(N>0\), there is a \(k\in \Z \) with \(k<-N\) such that \(a_k\neq 0\).
Suppose that \(f\) has an isolated singularity at \(P\). Then \(f\) has an essential singularity if and only if it does not have either a pole or removable singularity. By the previous four problems, \(f\) has an essential singularity if and only if both of the following conditions are false:
- \(a_k=0\) for all \(k<0\),
- The previous statement is false, but there is a \(N\in \N \) such that if \(k<-N\) then \(a_k=0\).
Thus, \(f\) has a pole or removable singularity if and only if there is a \(N\in \N \) such that if \(k<-N\) then \(a_k=0\) (with a pole if \(a_k\neq 0\) for some \(-N\leq k<0\) and a removable singularity otherwise). The negation of this statement is precisely the condition given in the problem statement.
Suppose that \(f\) has a zero of order \(k\) at \(P\). Show that \(\frac {1}{(z-P)^k}f(z)\) has a removable singularity at \(P\) and that its limit at \(P\) is not zero.
By assumption \(f\) is holomorphic in \(D(P,r)\) for some \(r>0\), and so by Theorem 3.3.1 we may write \(f(z)=\sum _{n=0}^\infty a_n (z-P)^n\) in \(D(P,r)\) for some coefficients \(a_n\).By definition of order, we have that \(a_k\neq 0\) and \(a_n=0\) for all \(n<k\). Thus \(f(z)=\sum _{n=k}^\infty a_n (z-P)^n\) for all \(z\in D(P,r)\).
Thus \(\frac {1}{(z-P)^k}f(z)=\sum _{n=k}^\infty a_n (z-P)^{n-k}=\sum _{m=0}^\infty a_{m+k} (z-P)^m\) for all \(z\in D(P,r)\setminus \{P\}\). In particular, the sum converges in \(D(P,r)\), and so \(\sum _{m=0}^\infty a_{m+k} (z-P)^m\) is holomorphic in \(D(P,r)\). Thus \(\frac {1}{(z-P)^k}f(z)\) has a removable singularity at \(z=P\). Furthermore, since holomorphic functions are continuous,
\begin{align*}\lim _{z\to P} \frac {1}{(z-P)^k}f(z) &= \lim _{z\to P}\sum _{m=0}^\infty a_{m+k} (z-P)^m = a_{0+k}=a_k\neq 0.\end{align*}
Suppose that \(f\) has a pole of order \(k\) at \(P\). Show that \((z-P)^kf(z)\) has a removable singularity at \(P\) and that its limit at \(P\) is not zero.
By assumption \(f\) is holomorphic in \(D(P,R)\setminus \{P\}\) for some \(R>0\). By Proposition 4.3.3 and definition of order, we have that there are coefficients \(a_k\) such that if \(z\in D(P,R)\setminus \{P\}\) then\begin{equation*}f(z)=\sum _{n=-k}^\infty a_n(z-P)^n\end{equation*}and that \(a_{-k}\neq 0\). Then \(g(z)=(z-P)^kf(z)\) has an isolated singularity at \(P\) because \(f(z)\), \((z-P)^k\) are holomorphic in \(D(P,R)\setminus \{P\}\), and so \(g\) must also have a Laurent series. It is
\begin{equation*}g(z)=\sum _{n=-k}^\infty a_n(z-P)^{k+n}=\sum _{m=0}^\infty a_{m-k}(z-P)^m\end{equation*}which converges in \(D(P,R)\setminus \{P\}\). Thus by 2290Problem 2290 \(g\) has a removable singularity at \(P\). By Lemma 3.2.10, the power series converges to a function holomorphic (thus continuous) on \(D(P,R)\), and in particular satisfies
\begin{equation*}\lim _{z\to P} g(z)=a_{-k}\neq 0\end{equation*}as desired.
Suppose that \(f\) is holomorphic in \(D(P,r)\setminus \{P\}\) and that \((z-P)^kf(z)\) has a removable singularity at \(P\) for \(k\in \N \). Show that either \(f\) has a removable singularity at \(P\) or \(f\) has a pole of order at most \(k\) at \(P\). If in addition \(\lim _{z\to P} (z-P)^k f(z)\neq 0\) then \(f\) has a pole of order exactly \(k\).
We may write \(f(z)=\sum _{n=-\infty }^\infty a_n (z-P)^n\) in \(D(P,r)\setminus \{P\}\). Then \((z-P)^k f(z)=\sum _{m=-\infty }^\infty a_{m-k} (z-P)^m\). Because this function has a removable singularity, we have by 2280Problem 2280 that \(a_{m-k}=0\) for all \(m<0\); thus, \(a_n=0\) if \(n<-k\).Thus \(f(z)=\sum _{n=-k}^\infty a_n (z-P)^n\) in \(D(P,r)\setminus \{P\}\), and so either \(a_n=0\) for all \(n<0\) and so \(f\) has a removable singularity at \(P\) by 2290Problem 2290, or there is an \(m\) with \(1\leq m\leq k\) such that \(a_{-m}\neq 0\) and \(a_n=0\) if \(n<-m\), and so by 2310Problem 2310 and the definition of order \(f\) has a pole of order \(m\leq k\).
Furthermore, \(\lim _{z\to P} (z-P)^k f(z)=a_{-k}\), and so if \(\lim _{z\to P} (z-P)^k f(z)\neq 0\), then \(a_{-k}\neq 0\) and so \(f\) has a pole of order exactly \(k\).
Suppose that \(f\) has a pole of order \(k> 0\) at \(P\). Let \(m\geq -k\) be an integer. Let the Laurent series for \(f\) in a punctured neighborhood of \(P\) be \(\sum _{n=-k}^\infty a_n (z-P)^n\). Show that
Suppose that \(f\) is holomorphic in \(D(P,r)\setminus \{P\}\) for some \(P\in \C \), \(r>0\), and that
has a removable singularity at \(z=P\) for some integers \(m\) and \(\ell \) with \(m+\ell \geq 0\). Show that \(f\) has a removable singularity or pole of order at most \(\ell \) at \(P\) and that
Suppose that \(f\) is holomorphic in \(D(P,r)\setminus \{P\}\) and that \((z-P)^\ell f(z)\) has a removable singularity at \(P\) for some \(\ell \geq 0\). Let \(f(z)=\sum _{n=-\infty }^\infty a_n (z-P)^n\) in \(D(P,r)\setminus \{P\}\). If \(m\geq \ell \), show that
If \(z\in D(P,r)\setminus \{P\}\) then\begin{equation*}(z-P)^\ell f(z)=\sum _{n=-\infty }^\infty a_n (z-P)^{n+\ell }=\sum _{n=-\infty }^\infty a_{n-\ell }(z-P)^n.\end{equation*}By 2280Problem 2280, we have that \(a_{n-\ell }=0\) for all \(n<0\), that is, \(a_n=0\) for all \(n<-\ell \). Thus
\begin{equation*}f(z)=\sum _{n=-\ell }^\infty a_n (z-P)^{n}.\end{equation*}We compute
\begin{align*} (z-P)^{-m}f(z)-\sum _{n=-\ell }^{m-1} a_n (z-P)^{n-m} &= \sum _{n=m}^\infty a_n (z-P)^{n-m} = \sum _{n=0}^\infty a_{n+m}(z-P)^n.\end{align*}The series converges for such \(z\) and so by Lemma 3.2.3 the radius of convergence is at least \(r\); thus, the series converges to a holomorphic (thus continuous) function on \(D(P,r)\). In particular,
\begin{gather*}\lim _{z\to P} \Bigl ((z-P)^{-k}f(z)-\sum _{n=-\ell }^{k-1} a_n (z-P)^{n-k}\Bigr ) \quad =\lim _{z\to P} \sum _{m=0}^\infty a_{m+k}(z-P)^m=a_k\end{gather*}as desired.
The principal part of the Laurent series \(\sum _{k=-\infty }^\infty a_k(z-P)^k\) is \(\sum _{k=-\infty }^{-1} a_k(z-P)^k\).
Let \(f(z)=z/(z-1)\). Find the Laurent series for \(f\) about \(z=1\) by direct computation.
Find the Laurent series for \(f(z)=z/(z-1)\) at \(P=1\) by using Problem 4.29.
\(\lim _{z\to 1} (z-1)f(z)=1\), and so \(f\) has a pole at \(1\) of order \(1\). Thus\begin{equation*}a_k=\lim _{z\to 1}\frac {1}{(1+k)!} \biggl (\frac {\partial }{\partial z}\biggr )^{1+k}(z).\end{equation*}Thus \(a_{-1}=\frac {1}{0!} z\vert _{z=1}=1\), \(a_0=\frac {1}{1!}\frac {\partial }{\partial z} z=1\), and \(a_k=0\) for any \(k>0\) because \(\bigl (\frac {\partial }{\partial z}\bigr )^{1+k}(z)=0\). Thus
\begin{equation*}f(z)=1+\frac {1}{z-1}.\end{equation*}
Find the Laurent series for \(f(z)=\frac {e^z}{(z-4)^2}\) at \(P=4\).
\(\lim _{z\to 4} (z-4)^2f(z)=e^4\) exists and is not zero, so \(f\) must have a pole of order \(2\) at \(4\). Thus\begin{equation*}a_k=\lim _{z\to 4}\frac {1}{(2+k)!} \biggl (\frac {\partial }{\partial z}\biggr )^{2+k}(e^z)=\frac {e^4}{(2+k)!}.\end{equation*}Thus
\begin{equation*}f(z)=\sum _{n=-2}^\infty \frac {e^4}{(n+2)!}(z-4)^{n}.\end{equation*}
Find the principal part of the Laurent series for \(f(z)=\frac {e^z}{(z-1)(z-3)^2}\) at \(P=3\).
\(\frac {e^z}{z-1}\) is holomorphic in a neighborhood of \(3\), so \(f\) has a pole of order \(2\) at \(P=3\). We compute\begin{equation*}a_{-2}=((z-3)^2f(z))\bigg \vert _{z=3}=\frac {e^3}{2}\end{equation*}and
\begin{equation*}a_{-1}=\frac {1}{1!} \frac {\partial }{\partial z}\frac {e^z}{z-1}\bigg \vert _{z=3} =\frac {e^z(z-2)}{(z-1)^2}\bigg \vert _{z=3} =\frac {e^3}{4}. \end{equation*}Thus the principal part of the Laurent series for \(f(z)=\frac {e^z}{(z-1)(z-3)^2}\) at \(P=3\) is
\begin{equation*}\frac {e^3/2}{(z-3)^2}+\frac {e^3/4}{z-3}.\end{equation*}
Find the principal part of the Laurent series for \(f(z)=\frac {e^z}{\sin z}\) at \(z=0\).
\(\sin z\) has an isolated zero at \(0\) and \(e^z\) is continuous and nonzero at \(0\), and so \(\lim _{z\to 0} \bigl |\frac {e^z}{\sin z}\bigr |=\infty \). Thus \(f\) has a pole at \(0\). Therefore, by Problems 2300Problem 2300, 2290Problem 2290 and 2310Problem 2310, \(zf(z)\) has either a pole or a removable singularity at \(0\).\begin{equation*}\lim _{\substack {x\to 0\\x\in \R }} x\frac {e^x}{\sin x}=1\end{equation*}by l’Hôpital’s rule in the real numbers. Therefore \(\lim _{z\to 0} |zf(z)|\neq \infty \) and so \(zf(z)\) does not have a pole at \(0\). It must have a removable singularity and satisfy \(\lim _{z\to 0} zf(z)=\lim _{\substack {x\to 0\\x\in \R }}xf(x)=1\). So by 2350Problem 2350 \(f\) has a pole of order \(1\) at \(0\), and by Problem 4.29 \(a_{-1}=1\). Thus the principal part of the Laurent series is \(\frac {1}{z}\).
Let \((X,d)\) be a metric space and let \(Y\subset X\) be a closed subset. Suppose that \(F\subseteq Y\) is relatively closed, that is, closed in \((Y,d)\). Show that \(F\) is also closed in \((X,d)\).
Let \((X,d)\) be a metric space and let \(Y\subset X\) be an open subset. Suppose that \(G\subseteq Y\) is relatively open, that is, open in \((Y,d)\). Show that \(G\) is also open in \((X,d)\).
Let \(r:[0,1]\to (0,\infty )\) and \(\theta :[0,1]\to \R \) be two \(C^1\) functions. Let \(\psi (t)=r(t)e^{i\theta (t)}\). Show that \(\theta '(t)=\im (\psi '(t)/\psi (t))\) and \(r'(t)/r(t)=\re (\psi '(t)/\psi (t))\).
Suppose that \(\psi \) is a closed curve. What can you say about \(r(0)\), \(r(1)\), \(\theta (0)\), and \(\theta (1)\)? What is the geometrical significance of the number \(\frac {1}{2\pi }(\theta (1)-\theta (0))\)?
We have that \(\psi (0)=\psi (1)\), so \(r(0)=|\psi (0)|=|\psi (1)|=r(1)\) and \(\theta (0)=\theta (1)+2n\pi \) for some \(n\in \Z \). The number \(n\) denotes the number of times the curve wraps around the origin counterclockwise.
Suppose that \(\psi \) is a closed curve. Show that
We call this number the index of \(\psi \) with respect to \(0\), or the winding number of \(\psi \) about \(0\).
We compute that\begin{align*} \frac {1}{2\pi }(\theta (1)-\theta (0)) &= \frac {1}{2\pi }\int _0^1 \theta '(t)\,dt = \frac {1}{2\pi } \int _0^1 \im \frac {\psi '(t)}{\psi (t)}\,dt \end{align*}and
\begin{align*} 0 = \frac {1}{2\pi }\left (\ln r(1)-\ln r(0)\right ) &= \frac {1}{2\pi }\int _0^1 \frac {r'(t)}{r(t)}\,dt = \frac {1}{2\pi } \int _0^1 \re \frac {\psi '(t)}{\psi (t)}\,dt . \end{align*}Thus,
\begin{align*} \frac {1}{2\pi }(\theta (1)-\theta (0)) &=\frac {1}{2\pi i} \int _0^1 \frac {\psi '(t)}{\psi (t)}\,dt = \frac {1}{2\pi i}\oint _{\psi } \frac {1}{\zeta }\,d\zeta . \end{align*}
Suppose \(\gamma :[0,1]\to \C \setminus \{0\}\) is a \(C^1\) curve. Then there exist two \(C^1\) functions \(r:[0,1]\to (0,\infty )\) and \(\theta :[0,1]\to \R \) such that \(\gamma (t)=r(t)e^{i\theta (t)}\) for all \(t\in [0,1]\).
Begin the proof of 2480Lemma 2480 by letting \(r(t)=|\gamma (t)|\) and showing that \(r\) is a \(C^1\) function. (In particular, show that \(\frac {r'(t)}{r(t)}=\re \frac {\gamma '(t)}{\gamma (t)}\).)
We have that\begin{equation*}r(t)=\sqrt {(\re \gamma (t))^2+(\im \gamma (t))^2}. \end{equation*}Furthermore, \(\re \gamma \) and \(\im \gamma \) are real-valued \(C^1\) functions. Because \(\gamma (t)\neq 0\) for all \(t\), we have that the function \(R(t)=(\re \gamma (t))^2+(\im \gamma (t))^2\) maps \([0,1]\) to \((0,\infty )\) and is \(C^1\).
The function \(h(t)=\sqrt {t}\) is \(C^1\) (in fact, \(C^\infty \)) on \((0,\infty )\), and so by the chain rule, \(r\) is \(C^1\). Furthermore, again by the chain rule
\begin{equation*}r'(t)=\frac {(\re \gamma (t))(\re \gamma '(t))+(\im \gamma (t))(\im \gamma '(t))}{\sqrt {(\re \gamma (t))^2+(\im \gamma (t))^2}}.\end{equation*}Conversely,
\begin{align*}\frac {\gamma '(t)}{\gamma (t)} &=\frac {(\re \gamma '(t))+i(\im \gamma '(t))} {(\re \gamma (t))+i(\im \gamma (t))} =\frac {(\re \gamma '(t)+i\im \gamma '(t))(\re \gamma (t)-i\im \gamma (t))} {|\gamma (t)|^2} \\&=\frac {\re \gamma '(t)\re \gamma (t)+\im \gamma '(t)\im \gamma (t)} {|\gamma (t)|^2} +i\frac {\im \gamma '(t)\re \gamma (t)-\re \gamma '(t)\im \gamma (t)} {|\gamma (t)|^2} \end{align*}and so \(\frac {r'(t)}{r(t)}=\frac {r'(t)}{|\gamma (t)|} =\re \frac {\gamma '(t)}{\gamma (t)}\), as desired.
Show that there exists a \(C^1\) function \(\theta :[0,1]\to \R \) such that \(\gamma (t)=r(t)e^{i\theta (t)}\) for all \(t\in [0,1]\), where \(r(t)=|\gamma (t)|\) as in the previous problem. Hint: There is a \(\theta _0\in \R \) such that \(\gamma (0)=r(0)e^{i\theta _0}\). What do you think \(\theta '(t)\) ought to equal?
Let \(\gamma \) be a \(C^1\) closed curve and let \(P\in \C \setminus \widetilde \gamma \). Then
is an integer.
Prove Lemma 4.5.5.
We define \(\Ind _\gamma (P)=\frac {1}{2\pi i}\oint _\gamma \frac {1}{\zeta -P}\,d\zeta \); this is the index of \(\gamma \) with respect to \(P\), or the winding number of \(\gamma \) about \(P\).
A connected open set \(\Omega \subseteq \C \) is simply connected if, whenever \(\gamma :[0,1]\to \Omega \) is a closed curve, we have that \(\gamma \) is homotopic to a point (that is, to some constant function \(\gamma _0:[0,1]\to \C \)).
Suppose that \(\Omega \subseteq \C \) is open and simply connected, \(\gamma :[0,1]\to \Omega \) is a \(C^1\) closed curve, and \(P\in \C \setminus \widetilde \gamma \) satisfies \(\Ind _\gamma (P)\neq 0\). Show that \(P\in \Omega \).
Suppose that \(P\notin \Omega \). Then \(f(\zeta )=1/(\zeta -P)\) is holomorphic in \(\Omega \), and so \(\oint \frac {1}{\zeta -P}\,d\zeta =0\) by 1420Problem 1420. Taking the contrapositive, if \(\Ind _\gamma (P)\neq 0\) then \(P\in \Omega \).
Let \(\gamma :[0,1]\to \C \) be a \(C^1\) closed curve. Show that \(\Ind _\gamma \) is a continuous function on \(\C \setminus \widetilde \gamma \).
Pick \(P\in \C \setminus \widetilde \gamma \) and \(\varepsilon >0\). Because \(\widetilde \gamma \) is compact (and therefore closed), there is an \(r>0\) such that \(D(P,r)\subset \C \setminus \widetilde \gamma \).Let \(\delta =\min \left (r/2, \frac {r^2\pi \varepsilon }{\ell (\gamma )+1}\right )\). If \(w\in D(P,\delta )\), then \(w\in D(P,r/2)\subset D(P,r)\subset \C \setminus \widetilde \gamma \) and
\begin{align*} \left |\Ind _\gamma (w)-\Ind _\gamma (P)\right | &= \left |\frac {1}{2\pi i}\oint _\gamma \frac {1}{z-P}-\frac {1}{z-w}\,dz\right | \\&=\frac {1}{2\pi } \left |\oint _\gamma \frac {P-w}{(z-P)(z-w)}\,dz\right | . \end{align*}\begin{align*} \left |\Ind _\gamma (w)-\Ind _\gamma (P)\right | &\leq \frac {1}{2\pi }\ell (\gamma ) \sup _{z\in \widetilde \gamma } \frac {|w-P|}{|z-P||z-w|}. \end{align*}By assumption \(|w-P|<\delta \). If \(z\in \widetilde \gamma \) then \(z\notin D(P,r)\) and so \(|z-P|\geq r\). By the triangle inequality \(|w-z|\geq |w-P|-r>r/2\). Thus
\begin{align*} \left |\Ind _\gamma (w)-\Ind _\gamma (P)\right | &< \frac {1}{2\pi }\ell (\gamma ) \frac {2}{r^2} \delta \leq \varepsilon \end{align*}as desired.
Show that \(\Ind _\gamma \) is constant on every connected component of \(\C \setminus \widetilde \gamma \).
Let \(\Omega \) be such a connected component. Let \(z\in \Omega \), \(n=\Ind _\gamma (z)\). Let \(f=\Ind _\gamma \big \vert _\Omega \).If \(w\in \Omega \) and \(f(w)\in D(n,1/2)\), then because \(f(w)\) is a (real) integer we must have that \(f(w)=n\). Thus
\begin{equation*}f^{-1}(\{n\})=f^{-1}(D(n,1/2)).\end{equation*}But \(\{n\}\) is a closed set and \(D(n,1/2)\) is an open set, and so \(f^{-1}(\{n\})=f^{-1}(D(n,1/2))\) must be both relatively open and relatively closed in \(\Omega \). By definition of connected set, this implies that \(\Omega =f^{-1}(\{n\})\) and so \(f\equiv n\) (and in particular is constant) on all of \(\Omega \).
Suppose that \(\gamma _1\) and \(\gamma _2\) are homotopic closed curves in \(\C \setminus \{P\}\). Show that \(\Ind _{\gamma _1}(P)=\Ind _{\gamma _2}(P)\).
The function \(f(\zeta )=\frac {1}{\zeta -P}\) is holomorphic in \(\C \setminus \{P\}\). Thus \(\Ind _{\gamma _1}(P)=\frac {1}{2\pi i}\oint _{\gamma _1} \frac {d\zeta }{\zeta -P}=\frac {1}{2\pi i}\oint _{\gamma _2} \frac {d\zeta }{\zeta -P}=\Ind _{\gamma _2}(P)\) by 1410Problem 1410.
Show that if \(\widetilde \gamma =\partial D(P,r)\) is a circle traversed once counterclockwise, then \(\Ind _\gamma (z)=1\) if \(z\in D(P,r)\) and \(\Ind _\gamma (z)=0\) if \(z\notin \overline D(P,r)\).
The case \(z\in D(P,r)\) follows immediately from the Cauchy integral formula (Theorem 2.4.2).If \(z\notin \overline D(P,r)\), then \(f(\zeta )=\frac {1}{\zeta -z}\) is holomorphic in \(D(P,|\zeta -P|)\supset \overline D(P,r)\), and so the result follows from the Cauchy integral theorem (Theorem 2.4.3).
Let \(\gamma :[0,1]\to \C \) be a \(C^1\) closed curve, and let \(t\in (0,1)\) be such that \(\gamma '(t)\neq 0\) and such that \(\gamma (t)\neq \gamma (s)\) for any \(s\in [0,1]\setminus \{t\}\).
If in addition \(\gamma \) is linear in a small neighborhood of \(t\) (that is, if \(\gamma (s)=\gamma (t)+(s-t)\gamma '(t)\) whenever \(|s-t|\) is sufficiently small), show that \(\Ind _\gamma (\gamma (t)+i\tau \gamma '(t))=\Ind _\gamma (\gamma (t)-i\tau \gamma '(t))+1\) whenever \(\tau >0\) is sufficiently small.
Show that the previous problem still holds even without the assumption of linearity.
An open set \(\Omega \subseteq \C \) is simply connected if every closed curve \(\gamma :[0,1]\to \Omega \) is homotopic to a point (that is, to a constant curve).
If \(\Omega \subseteq \C \) is open, \(P\in \Omega \), and \(f:\Omega \setminus \{P\}\to \C \) is holomorphic, then \(\Res _f(P)\) is defined to be the coefficient of \((z-P)^{-1}\) in the Laurent expansion of \(f\) about \(P\).
Suppose that \(\Omega \subseteq \C \) is open and simply connected, \(\{P_1,P_2,\dots ,P_n\}\subset \Omega \) is a set of \(n\) distinct points, \(\gamma :[0,1]\to \Omega \setminus \{P_1,P_2,\dots ,P_n\}\) is a \(C^1\) closed curve, and \(f:\Omega \setminus \{P_1,P_2,\dots ,P_n\}\to \C \) is holomorphic. Then
By 1420Problem 1420, Theorem 4.5.3 is true in the special case where \(n=0\), that is, where \(f\) is holomorphic in all of \(\Omega \).
Suppose that \(f(z)=\sum _{k=-\infty }^{-1} a_k (z-P)^k\) and that the Laurent series converges on all of \(\C \setminus \{P\}\). Show that Theorem 4.5.3 is true for this value of \(f\) in the case \(n=1\) and \(P=P_1\) (for any open set \(\Omega \owns P\) and any \(C^1\) closed curve \(\gamma :[0,1]\to \Omega \setminus \{P\}\)).
By 580Problem 580 and 620Problem 620, if \(k\neq -1\) then the function \((z-P)^k\) has a holomorphic antiderivative in \(\C \setminus \{P\}\), and so by Proposition 2.1.6, \(\oint _\gamma (z-P)^k\,dz=0\).Because \(\widetilde \gamma \) is compact we have that the Laurent series for \(f\) converges uniformly on \(\widetilde \gamma \). By 1580Memory 1580,
\begin{align*}\oint _\gamma f(z)\,dz &=\oint _\gamma \sum _{k=-\infty }^\infty a_k(z-P)^k\,dz =\sum _{k=-\infty }^\infty \oint _\gamma a_k(z-P)^k\,dz \\&=a_{-1}\oint _\gamma \frac {1}{z-P}\,dz\end{align*}and the result follows by definition of \(\Ind _\gamma (P)\).
Suppose that \(\Omega \subseteq \C \) is open, \(P\in \Omega \), and \(f:\Omega \setminus \{P\}\to \C \) is holomorphic. Show that the principal part of the Laurent series for \(f\) at \(P\) converges absolutely for all \(z\in \C \setminus \{P\}\) to a function holomorphic in \(\C \setminus \{P\}\).
Because \(\Omega \) is open, there is a \(r>0\) with \(D(P,r)\subseteq \Omega \). By Theorem 4.3.2, there is a Laurent series \(\sum _{k=-\infty }^\infty a_k (z-P)^k\) that converges absolutely to \(f(z)\) for \(z\in D(P,r)\setminus \{P\}\). The principal part is \(\sum _{k=-\infty }^{-1} a_k(z-P)^k\); by definition of convergence of a doubly infinite series, it converges absolutely for \(z\in D(P,r)\setminus \{P\}\).If \(|w|>1/r\), then the series converges at \(z=P+1/w\), and by reindexing we see that \(\sum _{\ell =1}^{\infty } a_{-\ell }w^\ell \) converges. Thus by Lemma 3.2.3, \(\sum _{\ell =1}^{\infty } a_{-\ell }\zeta ^\ell \) converges for all \(\zeta \in \C \). Reindexing again we see that \(\sum _{k=-\infty }^{-1} a_k(z-P)^k\) converges for all \(z\in \C \setminus \{P\}\).
By 2100Problem 2100, \(\sum _{k=-\infty }^{-1} a_k (z-P)^k\) is holomorphic in the interior of the annulus of convergence, that is, in \(\C \setminus \{P\}\).
Suppose that \(h\) is holomorphic in \(D(P,r)\) and that \(g\) is holomorphic in \(D(P,r)\setminus \{P\}\). If \(f=g+h\) in \(D(P,r)\setminus \{P\}\), show that \(\Res _f(P)=\Res _g(P)\).
\(f\) is holomorphic in \(D(P,r)\setminus \{P\}\). By Theorem 3.3.1 and Theorem 4.3.2, there are constants \(a_k\), \(b_k\), and \(c_k\) such that\begin{gather*}f(z)=\sum _{k=-\infty }^\infty a_k(z-P)^k, \quad g(z)=\sum _{k=0}^\infty b_k(z-P)^k, \quad h(z)=\sum _{k=-\infty }^\infty c_k(z-P)^k \end{gather*}for all \(z\in D(P,r)\setminus \{P\}\). Define \(b_k=0\) for all \(k<0\); then \(g(z)=\sum _{k=-\infty }^\infty b_k(z-P)^k\) and so
\begin{align*}\sum _{k=-\infty }^\infty a_k(z-P)^k &=f(z)=g(z)+h(z) =\sum _{k=-\infty }^\infty (b_k+c_k)(z-P)^k\end{align*}for all \(z\in D(P,r)\setminus \{P\}\). By Proposition 4.2.4, we have that \(a_k=b_k+c_k\) for all \(k\); in particular, \(\Res _f(P)=a_{-1}=b_{-1}+c_{-1}=c_{-1}=\Res _h(P)\).
Prove Theorem 4.3.2.
By 2590Memory 2590 the theorem is true if \(n=0\).
Because \(\Omega \setminus \bigl (\{P_1,P_2,\dots ,P_n\}\setminus \{P_k\}\bigr )\) is open, for each \(1\leq k\leq n\) there is a \(r_k>0\) such that \(D(P_k,r_k)\subseteq \Omega \setminus \bigl (\{P_1,P_2,\dots ,P_n\}\setminus \{P_k\}\bigr )\), that is, such that \(D(P_k,r_k)\setminus \{P_k\}\subseteq \Omega \setminus \{P_1,P_2,\dots ,P_n\}\). Observe that \(f\) is holomorphic in \(D(P_k,r_k)\setminus \{P_k\}\) for each \(k\).
Suppose \(n\geq 1\) and the theorem is true for \(n-1\). Then there are coefficients \(a_k\) such that
\begin{equation*}f(z)=\sum _{k=-\infty }^\infty a_k(z-P_n)^k\text { for all $z\in D(P_n,r_n)\setminus \{P\}$.}\end{equation*}Let \(g(z)=\sum _{k=-\infty }^{-1} a_k(z-P_n)^k\); by 2610Problem 2610, \(g\) is holomorphic on \(\C \setminus \{P_n\}\), and by 2600Problem 2600,
\begin{equation*}\oint _\gamma g=2\pi i \Ind _\gamma (P_n)\,\Res _g(P_n).\end{equation*}Observe that \(\Res _g(P_n)=a_{-1}=\Res _f(P_n)\).
Define \(h:\Omega \setminus \{P_1,\dots ,P_{n-1}\}\to \C \) by
\begin{equation*}h(z)=\begin {cases}f(z)-g(z),&z\neq P_n,\\ a_0,&z=P_n.\end {cases}\end{equation*}We then have that \(h(z)=\sum _{k=0}^\infty a_k(z-P)^k\) and the series converges for all \(z\in D(P_n,r_n)\), and so by Lemma 3.2.10, \(h\) is holomorphic in \(D(P_n,r_n)\), and thus in \(\Omega \setminus \{P_1,\dots ,P_{n-1}\}\). Thus by our induction hypothesis
\begin{equation*}\oint _{\gamma } h=2\pi i\sum _{k=1}^{n-1}\Res _h(P_k)\Ind _\gamma (P_k).\end{equation*}Because \(P_n\notin \widetilde \gamma \) we have that \(f=g+h\) on \(\widetilde \gamma \), and so
\begin{equation*}\oint _{\gamma } f=2\pi i\Bigl (\sum _{k=1}^{n-1}\Res _h(P_k)\Ind _\gamma (P_k)+\Res _f(P_n)\Ind _\gamma (P_k)\Bigr ).\end{equation*}The proof follows by 2620Problem 2620.
The best way to draw contours in LaTeX is probably the TikZ package:
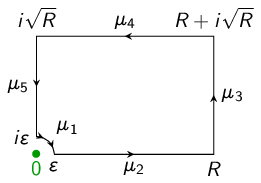
If you would like to use the above picture on your homework, you may generate it as follows.
Add the following code to your document preamble (that is, put the following code between the \documentclass{article} and the \begin{document}):
\usepackage{tikz}
\usetikzlibrary{decorations.pathreplacing, decorations.markings, positioning}
\tikzset{
% style to apply some styles to each segment of a path
on each segment/.style={
decorate,
decoration={
show path construction,
moveto code={},
lineto code={
\path [#1]
(\tikzinputsegmentfirst) -- (\tikzinputsegmentlast);
},
curveto code={
\path [#1] (\tikzinputsegmentfirst)
.. controls
(\tikzinputsegmentsupporta) and (\tikzinputsegmentsupportb)
..
(\tikzinputsegmentlast);
},
closepath code={
\path [#1]
(\tikzinputsegmentfirst) -- (\tikzinputsegmentlast);
},
},
},
% style to add an arrow in the middle of a path
mid arrow/.style={postaction={decorate,decoration={
markings,
mark=at position .5 with {\arrow[#1]{stealth}}
}}},
}
Add the following code in your document body, where you want the picture to appear:
\begin{tikzpicture}
%
\node at (0,0) {$\bullet$};
\node [below] at (0,0) {$0$};
%
\path [draw,postaction={on each segment={mid arrow}}]
(0.3,0) node [below] {$\varepsilon$}
-- node [below] {$\mu_2$}
(3,0) node [below] {$R$}
-- node [right]{ $\mu_3$}
(3,2) node [above] {$R+i\sqrt{R}$}
-- node [above] {$\mu_4$}
(0,2) node [above] {$i\sqrt{R}$}
-- node [left] {$\mu_5$}
(0,0.3) node [left] {$i\varepsilon$}
arc (90:45:.3) node [above right] {$\mu_1$}
arc (45:1:0.3)
;
\end{tikzpicture}
Note: The code in the \tikzset{} and \usetikzlibrary{}, as well as the complicated
command
\path [draw,postaction={on each segment={mid arrow}}]
(instead of the simple command \draw) produce arrowheads on the contours. For the
sake of simplicity, when TikZ code is provided in the following examples, this will be
omitted; the code will be displayed as
\usepackage{tikz}
...
\begin{tikzpicture}
\node at (0,0) {$\bullet$};
\node [below] at (0,0) {$0$};
%
\draw
(0.3,0) node [below] {$\varepsilon$}
-- node [below] {$\mu_2$}
(3,0) node [below] {$R$}
-- node [right]{ $\mu_3$}
(3,2) node [above] {$R+i\sqrt{R}$}
-- node [above] {$\mu_4$}
(0,2) node [above] {$i\sqrt{R}$}
-- node [left] {$\mu_5$}
(0,0.3) node [left] {$i\varepsilon$}
arc (90:45:.3) node [above right] {$\mu_1$}
arc (45:1:0.3)
;
\end{tikzpicture}
By Problem 4.29, if \(f\) has a pole of order \(k\) at \(P\), then
In particular, if \(f\) has a simple pole at \(P\), then
L’Hôpital’s rule is valid for quotients of meromorphic functions.
That is, let \(r>0\) and \(P\in \C \). Suppose that \(f\) and \(g\) are both holomorphic in \(D(P,r)\setminus \{P\}\), and that neither \(f\) nor \(g\) has an essential singularity at \(P\). Finally suppose that \(g\) is not a constant in \(D(P,r)\setminus \{P\}\).
Then there is a \(\varrho \) with \(0<\varrho \leq r\) such that \(g(z)\neq 0\neq g'(z)\) for all \(z\in D(P,\varrho )\setminus \{P\}\). Furthermore, the functions \(f/g\) and \(f'/g'\), which are holomorphic in \(D(P,\varrho )\setminus \{P\}\), do not have essential singularities at \(P\).
Finally, if \(f\) and \(g\) both have poles at \(P\) or if \(\lim _{z\to P} f(z)=0=\lim _{z\to P} g(z)\), then \(f/g\) has a pole at \(P\) if and only if \(f'/g'\) has a pole at \(P\), and if \(f'/g'\) has a removable singularity then \(\lim _{z\to P} f(z)/g(z)=\lim _{z\to P} f'(z)/g'(z)\).
Consider the integral \(\int _{-\infty }^\infty \frac {x^2}{x^4+4}\,dx\). Write down a family of closed \(C^1\) curves \(\gamma _R\) and a function \(f\) holomorphic in a neighborhood of \(\widetilde \gamma _R\) such that \(\lim _{R\to \infty }\oint _{\gamma _R} f=\int _{-\infty }^\infty \frac {x^2}{x^4+4}\,dx\).
Then find \(\int _{-\infty }^\infty \frac {x^2}{x^2+4} dx\) by finding \(\oint _{\psi _R} f\) for all \(R\) large enough.
Compute \(\int _{-\infty }^\infty \frac {\cos x}{x^2+4} \,dx\). Hint: Recall that \(\re \int _a^b f(x)\,dx=\int _a^b \re f(x)\,dx\).
Let \(f(z)=\frac {e^{iz}}{z^2+4}\). Then \(f\) has two poles, at \(\pm 2i\), and both are of order one.Let \(\psi _R:[-R,R]\to \C \) be given by \(\psi _R(t)=t\). Let \(\theta _R:[0,\pi ]\to \C \) be given by \(\theta _R(t)=Re^{it}\). Then \(\psi _R\) and \(\theta _R\) are two \(C^1\) curves with \(\psi _R(R)=\theta _R(0)\), and so we can combine them using 1050Problem 1050 to get a \(C^1\) curve \(\gamma _R:[-1,1]\to \C \). Because \(\gamma _R(-1)=\psi _R(-R)=-R=Re^{i\pi }=\theta _R(\pi )=\gamma _R(1)\), \(\gamma _R\) is a closed curve.
Here are the traces of the curves \(\psi _R\) and \(\theta _R\) together with the singularities of \(f\):
If you would like to use the above picture on your homework, you may generate it with the following code:
\usepackage{tikz} ... \begin{tikzpicture} [scale=0.3] \node at (0,4) {$\bullet$}; \node [below] at (0,4) {$2i$}; % \node at (0,-4) {$\bullet$}; \node [above] at (0,-4) {$-2i$}; % \draw (-3,0)-- node [below] {$\widetilde\psi_R$} (3,0) node [below] {$R$} arc (0:45:3) node [above right] {$\widetilde\theta_R$} arc (45:90:3) arc (90:180:3); \end{tikzpicture}Then
\begin{align*}\int _{-\infty }^\infty \frac {\cos x}{x^2+4}\,dx &=\lim _{R\to \infty }\int _{-R}^R \frac {\cos x}{x^2+4}\,dx =\lim _{R\to \infty }\int _{-R}^R \frac {\re e^{ix}}{x^2+4}\,dx \\&=\lim _{R\to \infty }\re \int _{-R}^R \frac { e^{ix}}{x^2+4}\,dx =\lim _{R\to \infty } \re \oint _{\psi _R} f.\end{align*}As before
\begin{equation*}\biggl |\oint _{\theta _R} f\biggr | \leq \ell (\theta _R) \sup _{\widetilde \theta _R} |f| \leq \pi R\frac {1}{R^2-4}\end{equation*}and so \(\lim _{R\to \infty } \oint _{\theta _R} f=0\).
By 1050Problem 1050 \(\oint _{\gamma _R} f=\oint _{\theta _R} f+\oint _{\psi _R} f\), and so
\begin{equation*}\int _{-\infty }^\infty \frac {\cos x}{x^2+4}\,dx =\lim _{R\to \infty } \re \oint _{\gamma _R} f.\end{equation*}But by Theorem 4.5.3, if \(R>2\) then
\begin{equation*}\oint _{\gamma _R} f = 2\pi i \Res _f(2i) \Ind _{\gamma _R}(2i)=2\pi i\Res _f(2i).\end{equation*}We find
\begin{align*}\Res _f(2i) &=\lim _{z\to 2i} (z-2i)f(z)=\lim _{z\to 2i} \frac {(z-2i)e^{iz}}{z^2+4} =\lim _{z\to 2i}\frac {e^{iz}}{z+2i} =\frac {e^{-2}}{4i}.\end{align*}Thus
\begin{equation*}\int _{-\infty }^\infty \frac {\cos x}{x^2+4}\,dx =\re 2\pi i \frac {e^{-2}}{4i}=\frac {e^{-2}\pi }{2}.\end{equation*}
Compute \(\int _{0}^\infty \frac {\sin x}{x}\,dx\) by using the following contour:
The code for generating this picture is given in the previous section.
(A verbatim presentation of Example 4.6.3 will not be accepted, but you may read Example 4.6.3 for inspiration.)
Let \(f(z)=\frac {e^{iz}}{z}\).Define the curves \(\mu _j\) to have the traces given above, with the curve \(\mu \) given by 1050Problem 1050 oriented counterclockwise.
Then \(\oint _\mu f =0\) because \(f\) is holomorphic on \(\C \setminus \{0\}\).
By definition of line integral and 1010Problem 1010, and parameterizing the reverse of \(\mu _1\) by \(\hat \mu _1(t)=\varepsilon e^{it}\), we see that
\begin{equation*}\oint _{\mu _1} f = -\int _0^{\pi /2} f(\varepsilon e^{it}) i\varepsilon e^{it}\,dt = -i\int _0^{\pi /2}e^{i\varepsilon e^{it}}\,dt .\end{equation*}Because \(e^{i\varepsilon e^{it}}\to 1\), uniformly in \(t\), as \(\varepsilon \to 0^+\), we have that
\begin{equation*}\lim _{\varepsilon \to 0^+}\oint _{\mu _1} f = -i\frac {\pi }{2}.\end{equation*}By the definition of line integral and of integral of complex function, using the natural parameterization of \(\mu _2\), we have that
\begin{equation*}\int _0^\infty \frac {\sin x}{x}\,dx = \im \lim _{R\to \infty } \lim _{\varepsilon \to 0^+} \oint _{\mu _2} f.\end{equation*}We compute
\begin{align*} \left |\oint _{\mu _3} f\right | &\leq \ell (\mu _3)\sup _{\widetilde \mu _3} |f| =\sqrt {R}\cdot \frac {1}{R}=\frac {1}{\sqrt {R}} ,\\ \left |\oint _{\mu _4} f\right | &\leq \ell (\mu _4)\sup _{\widetilde \mu _4} |f| =R\cdot \frac {e^{-\sqrt {R}}}{\sqrt {R}} \end{align*}and so \(\lim _{R\to \infty } \oint _{\mu _3} f=\lim _{R\to \infty } \oint _{\mu _4} f=0\).
Finally, parameterizing the reverse of \(\mu _5\) by \(\hat \mu _5(t)=it\),
\begin{equation*}\oint _{\mu _5} f =-\int _\varepsilon ^R f(it)\,i\,dt = -\int _\varepsilon ^R \frac {e^{-t}}{it} i\,dt \end{equation*}is an entirely real integral, and so \(\im \oint _{\mu _5} f=0\).
Combining the above results, we have that
\begin{align*} 0&=\lim _{R\to \infty }\lim _{\varepsilon \to 0^+}\im \oint _\mu f \\&= \lim _{\varepsilon \to 0^+}\im \oint _{\mu _1} f +\lim _{R\to \infty }\lim _{\varepsilon \to 0^+}\im \oint _{\mu _2} f \\&\qquad +\lim _{R\to \infty }\im \oint _{\mu _3} f +\lim _{R\to \infty }\im \oint _{\mu _4} f +0 \\&=-\frac {\pi }{2}+\int _0^\infty \frac {\sin x}{x}\,dx. \end{align*}Thus
\begin{equation*}\int _0^\infty \frac {\sin x}{x}\,dx=\frac {\pi }{2}.\end{equation*}
If \(\Omega =\C \setminus \{te^{i\theta _0}:t\in \R ,\>t\geq 0\}\), and if \(F:\Omega \to \C \) is holomorphic and satisfies \(\frac {\partial }{\partial z} F(z)=\frac {1}{z}\) in \(\Omega \), then there is a constant \(C\in \C \) such that, if \(r>0\) and \(\theta _0<\theta <\theta _0+2\pi \), then
Furthermore, there is a constant \(\alpha \) such that \(\exp (F(z))=\alpha z\) for all \(z\in \Omega \).
Let \(n\in \N \) and let \(\theta _0\in \R \). Define \(z^{1/n}\) with branch cut at angle \(\theta _0\) by \((re^{i\theta })^{1/n}=r^{1/n} e^{i\theta /n}\) for all \(r>0\) and all \(\theta _0\leq \theta <\theta _0+2\pi \). Show that \(z^{1/n}\) is holomorphic on \(\C \setminus \{te^{i\theta _0}:t\in \R ,\>t\geq 0\}\) and that \(\p {z} z^{1/n}=\frac {1}{n (z^{1/n})^{n-1}}\).
That \(z^{1/n}\) is well defined follows from Problem 1.25 in your book and from 370Problem 370.The domain \(\Omega =\C \setminus \{te^{i\theta _0}:t\in \R ,\>t\geq 0\}\) is simply connected, and thus by 1420Problem 1420, if \(\gamma \) is a \(C^1\) closed curve in \(\Omega \) and \(f\) is holomorphic then \(\oint _\gamma f=0\). Thus by 1470Problem 1470 the function \(f(z)=1/z\) has a holomorphic antiderivative in \(\Omega \). By the above homework problem we have that, if \(F(re^{i\theta })=\ln r+i\theta \) whenever \(r>0\) and \(\theta _0<\theta <\theta _0+2\pi \), then \(F\) is the holomorphic antiderivative of \(1/z\) in \(\Omega \); in particular, \(F\) is indeed holomorphic in \(\Omega \).
Observe that
\begin{equation*}z^{1/n} = \exp (F(z)/n)\end{equation*}and so \(z^{1/n}\) is holomorphic, as it is a composition of holomorphic functions.
Find \(\int _{0}^\infty \frac {x^{1/3}}{x^2+2x+1}\,dx\).
If \(0<\varepsilon <\pi /2<R<\infty \), define the contours \(\eta _k\) as shown below. \(\eta _2\) is oriented counterclockwise, and \(\widetilde \eta _4\) is a subset of the circle of radius \(1/R\) centered at \(0\).
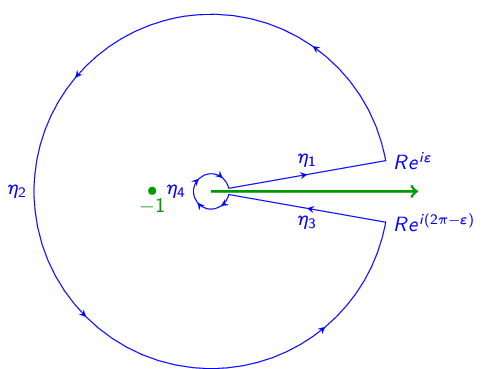
\usepackage{tikz} ... \begin{tikzpicture} \draw (10:0.3) -- node [above] {$\eta_1$} (10:3) node [right]{$Re^{i\varepsilon}$} arc (10:180:3) node[left] {$\eta_2$} arc (180:350:3) node [right]{$Re^{i(2\pi-\varepsilon)}$} -- node [below] {$\eta_3$} (-10:0.3) arc (-10:-180:0.3) node [left] {$\eta_4$} arc (-180:-350:0.3); \end{tikzpicture}Let \(f(z)=\frac {z^{1/3}}{(z+1)^2}\) where the branch cut of \(z^{1/3}\) is taken to be at \(\theta _0=0\), that is, the positive real axis.
We may then compute that \(f\) is holomorphic in a neighborhood of \(\widetilde \eta \) for any such \(\varepsilon \) and \(R\) and has only one singularity in the interior of \(\eta \), namely \(z=-1\). Because \(f\) has a pole of order \(2\) at \(z=-1\), we compute using Problem 4.29 that
\begin{equation*}\Res _f(-1) = \lim _{z\to -1}\p {z} z^{1/3} = \frac {1}{3}e^{-2\pi i/3} \end{equation*}and so
\begin{equation*} \frac {2\pi i}{3}e^{-2\pi i/3} = \oint _\eta f = \oint _{\eta _1} f+\oint _{\eta _2} f+\oint _{\eta _3} f+\oint _{\eta _4} f.\end{equation*}By Proposition 2.1.8, if \(R>1\) then
\begin{equation*}\biggl |\oint _{\eta _2} f\biggr |\leq 2\pi R \frac {\sqrt [3]{R}}{(R-1)^2}, \qquad \biggl |\oint _{\eta _4} f\biggr |\leq 2\pi \frac {1}{R}\frac {\sqrt [3]{1/R}}{(1-1/R)^2} \end{equation*}and so \(\lim _{R\to \infty } \oint _{\eta _2} f+\oint _{\eta _4} f=0\). Thus
\begin{equation*} \frac {2\pi i}{3}e^{-2\pi i/3} = \lim _{R\to \infty }\oint _{\eta _1} f+\oint _{\eta _3} f.\end{equation*}By definition of line integral,
\begin{equation*}\oint _{\eta _1} f=\int _{1/R}^R \frac {\sqrt [3]{t}e^{i\varepsilon /3}}{(te^{i\varepsilon }+1)^2} e^{i\varepsilon } dt \end{equation*}and so
\begin{align*}\int _0^\infty \frac {x^{1/3}}{x^2+2x+1}\,dx &= \lim _{R\to \infty } \int _{1/R}^R \frac {x^{1/3}}{x^2+2x+1}\,dx =\lim _{R\to \infty } \lim _{\varepsilon \to 0^+} \oint _{\eta _1} f.\end{align*}By 1010Problem 1010
\begin{align*}\oint _{\eta _3} f &= -\int _{1/R}^R \frac {\sqrt [3]{t}e^{i(2\pi /3-\varepsilon /3)}} {(te^{i(2\pi -\varepsilon )}+1)^2} e^{i(2\pi -\varepsilon )} dt = e^{-i\pi /3}\int _{1/R}^R \frac {\sqrt [3]{t}e^{i(-\varepsilon /3)}} {(te^{i(2\pi -\varepsilon )}+1)^2} e^{i(2\pi -\varepsilon )} dt \end{align*}and so
\begin{align*} e^{-\pi i/3}\int _0^\infty \frac {x^{1/3}}{x^2+2x+1}\,dx &= e^{-\pi i/3}\lim _{R\to \infty } \int _{1/R}^R \frac {x^{1/3}}{x^2+2x+1}\,dx = \lim _{R\to \infty } \lim _{\varepsilon \to 0^+} \oint _{\eta _3} f.\end{align*}Thus
\begin{align*} (1+e^{-i\pi /3})\int _0^\infty \frac {x^{1/3}}{x^2+2x+1}\,dx &=\lim _{R\to \infty } \lim _{\varepsilon \to 0^+} \oint _{\eta _1} f+\oint _{\eta _3} f =\frac {2\pi i}{3}e^{-2\pi i/3}\end{align*}and so
\begin{align*} \int _0^\infty \frac {x^{1/3}}{x^2+2x+1}\,dx &=\frac {2\pi i}{3}e^{-2\pi i/3} \frac {1}{1+e^{-i\pi /3}} =\frac {\pi }{3} \frac {2}{e^{i\pi /6}+e^{-i\pi /6}} \\&=\frac {\pi }{3\cos (\pi /6)} =\frac {2\pi }{3\sqrt {3}} \end{align*}
Use the calculus of residues to compute \(\int _0^\infty \frac {dx}{x^2+5x+6}\).
Define \(\log :\C \setminus [0,\infty )\to \C \) by \(\log (re^{i\theta })=\ln r+i\theta \) whenever \(r>0\) and \(0<\theta <2\pi \); this is well defined by 370Problem 370, and as shown in the solution to 2680Problem 2680 is holomorphic on \(\C \setminus [0,\infty )\).Define \(g(z)=\frac {\log z}{z^2+5z+6}\). Let \(\eta _k\) be as in the previous problem.
We can show as usual that \(\lim _{R\to \infty } \oint _{\eta _2} g=\lim _{R\to \infty } \oint _{\eta _4} g=0\).
Observe that
\begin{equation*}\oint _{\eta _1} g = \int _{1/R}^R \frac {\log t+i\varepsilon }{t^2e^{2i\varepsilon }+5te^{i\varepsilon }+6}\,dt\end{equation*}and
\begin{equation*}\oint _{\eta _3} g = -\int _{1/R}^R \frac {\log t+2\pi i -i\varepsilon }{t^2e^{-2i\varepsilon }+5te^{-i\varepsilon }+6}\,dt.\end{equation*}Fix \(R\). The integrands converge uniformly as \(\varepsilon \to 0^+\), and so
\begin{equation*}\lim _{\varepsilon \to 0^+}\biggl (\oint _{\eta _1} g+\oint _{\eta _3} g\biggr ) = \int _{1/R}^R \frac {-2\pi i}{t^2+5t+6}\,dt.\end{equation*}Thus
\begin{align*} \int _0^\infty \frac {1}{x^2+5x+6}\,dx &= -\frac {1}{2\pi i} \lim _{R\to \infty } \lim _{\varepsilon \to 0^+} \oint _\eta g \\&= -\Res _g(-2)-\Res _g(-3) \\&=-\frac {\log 2 + i\pi }{-2+3} - \frac {\log 3+i\pi }{-3+2} \\&=-\log 2+\log 3. \end{align*}
Find \(\int _0^\infty \frac {\sqrt [5]{x}}{x^7+1}\,dx\).
Let \(\eta _1\), \(\eta _2\), \(\eta _3\), and \(\eta _4\) (the small unlabeled contour) be as shown, and let \(\eta \) be the contour obtained by 1050Problem 1050.
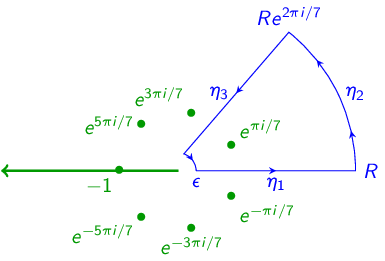
\usepackage{tikz} ... \begin{tikzpicture} \draw (0:0.3) node [below] {$\epsilon$} -- node [below] {$\eta_1$} (0:3) node [right]{$R$} arc (0:25.714285:3) node[right] {$\eta_2$} arc (25.714285:51.428571:3) node [above] {$Re^{2\pi i/7}$} -- node [left] {$\eta_3$} (72:0.3) arc (72:0:0.3) ; \draw [very thick, ->(0,0)--(-3,0); \node [above right] at (25.714285:1) {$e^{\pi i/7}$}; \node at (25.714285:1) {$\bullet$}; \node [above left] at (77.142857:1) {$e^{3\pi i/7}$}; \node at (77.142857:1) {$\bullet$}; \node [left] at (128.571428:1) {$e^{5\pi i/7}$}; \node at (128.571428:1) {$\bullet$}; \node [below left] at (180:1) {$-1$}; \node at (180:1) {$\bullet$}; \node [below right] at (-25.714285:1) {$e^{-\pi i/7}$}; \node at (-25.714285:1) {$\bullet$}; \node [below] at (-77.142857:1) {$e^{-3\pi i/7}$}; \node at (-77.142857:1) {$\bullet$}; \node [below left] at (-128.571428:1) {$e^{-5\pi i/7}$}; \node at (-128.571428:1) {$\bullet$}; \end{tikzpicture}
Let \(f(z)=\frac {z^{1/5}}{z^7+1}\), where \(z^{1/5}=r^{1/5}e^{i\theta /5}\) where \(r\) and \(\theta \) are the unique real numbers with \(r\geq 0\), \(-\pi < \theta <\pi \) and \(z=re^{i\theta }\). A standard argument shows that
\begin{equation*}\lim _{R\to \infty }\oint _{\eta _2} f = 0 =\lim _{\varepsilon \to 0^+}\oint _{\eta _4} f\end{equation*}and
\begin{equation*}\oint _\eta f = 2\pi i\Res _f(e^{\pi i/7}).\end{equation*}Thus
\begin{equation*}2\pi i\Res _f(e^{\pi i/7}) = \lim _{R\to \infty ,\varepsilon \to 0^+} \oint _{\eta _1} f +\oint _{\eta _2} f.\end{equation*}We compute that
\begin{align*} \oint _{\eta _1} f &= \int _\varepsilon ^R \frac {x^{1/5}}{x^7+1}dx,\\ \oint _{\eta _2} f &= -\int _\varepsilon ^R \frac {(xe^{2\pi i/7})^{1/5}}{x^7+1}e^{2\pi i/7}dx\\ &= -e^{12\pi i/35}\int _\varepsilon ^R \frac {x^{1/5} }{x^7+1}dx\\ \end{align*}so
\begin{align*} (1-e^{12\pi i/35})\int _0^\infty \frac {x^{1/5}}{x^7+1}\,dx =2\pi i\Res _f(e^{\pi i/7}) .\end{align*}We now consider
\begin{equation*}\lim _{z\to e^{i\pi /7}} (z-e^{i\pi /7})f(z) =\lim _{z\to e^{i\pi /7}} \frac {(z-e^{i\pi /7})z^{1/5}}{z^7+1}.\end{equation*}The numerator and denominator are both holomorphic in a neighborhood of \(e^{i\pi /7}\) and equal zero at \(e^{i\pi /7}\). Thus we may apply l’Hôpital’s rule. We observe that
\begin{equation*}\p {z} z^{1/n}=\p {x} z^{1/n}\end{equation*}by Proposition 1.4.3, and so \(\p {z}z^{1/n}=\frac {1}{n}z^{1/n-1}\) if \(z\) is a positive real number. By Corollary 3.6.3 this implies that \(\p {z}z^{1/n}=\frac {1}{n}z^{1/n-1}\) for all \(z\) in the domain of \(z^{1/n}\). Thus
\begin{align*} \lim _{z\to e^{i\pi /7}} (z-e^{i\pi /7})f(z) &=\lim _{z\to e^{i\pi /7}} \frac {z^{1/5}+(1/5)z^{-4/5}(z-e^{i\pi /7})}{7z^6} =\frac {e^{i\pi /35}}{7e^{6i\pi /7}} .\end{align*}Thus \(f\) has a simple pole at \(e^{i\pi /7}\) (this may also be seen by factoring the denominator) and the residue is given by the above limit, and so
\begin{align*} \int _0^\infty \frac {x^{1/5}}{x^7+1}\,dx &= \frac {2\pi i}{1-e^{12\pi i/35}}\frac {e^{i\pi /35}}{7e^{6i\pi /7}} \\&=\frac {2 i} {e^{29i\pi /35}-e^{41\pi i/35}}\frac {\pi }{7} .\end{align*}But \(e^{41\pi i/35}=e^{41\pi i/35-2\pi i}=e^{-29\pi i/35}\), so
\begin{align*} \int _0^\infty \frac {x^{1/5}}{x^7+1}\,dx &= \frac {2 i} {e^{29i\pi /35}-e^{-29\pi i/35}}\frac {\pi }{7} =\frac {\pi }{7}\csc (29\pi /35) .\end{align*}Because \(\sin (x+\pi )=-\sin (x)\) for all \(x\in \R \), we compute that \(\csc (29\pi /35) = -\csc (29\pi /35-\pi )=-\csc (-6\pi /35)=\csc (6\pi /35)\). Thus
\begin{align*} \int _0^\infty \frac {x^{1/5}}{x^7+1}\,dx &= \frac {\pi }{7}\csc (6\pi /35) .\end{align*}
Compute \(\int _0^{2\pi } \frac {d\theta }{3+\sin \theta }\).
Recall that \(\sin \theta = \frac {e^{i\theta }-e^{-i\theta }}{2i}\). Thus,\begin{align*} \int _0^{2\pi } \frac {d\theta }{3+\sin \theta } &=\int _0^{2\pi } \frac {2i\,d\theta }{6i+2i\sin \theta } \\&=\int _0^{2\pi } \frac {2i\,d\theta }{6i+e^{i\theta }-e^{-i\theta }} \\&=\int _0^{2\pi } \frac {2ie^{i\theta }\,d\theta }{6ie^{i\theta }+e^{2i\theta }-1} \\&=\int _0^{2\pi } \frac {2ie^{i\theta }\,d\theta }{6ie^{i\theta }+(e^{i\theta })^2-1} . \end{align*}Let \(\gamma (t)=e^{it}\), \(0\leq t\leq 2\pi \). Let \(f(z)=\frac {2}{6iz+z^2-1}\). Then
\begin{equation*}\oint _\gamma f = \int _0^{2\pi } f(\gamma (t))\gamma '(t)\,dt =\int _0^{2\pi } \frac {2}{6ie^{it}+e^{2it}-1} ie^{it}\,dt.\end{equation*}Thus
\begin{align*} \int _0^{2\pi } \frac {d\theta }{3+\sin \theta } &=\oint _\gamma f. \end{align*}The function \(f\) has poles at \((-3\pm \sqrt {8})i\). The point \((-3-\sqrt 8)i\) lies outside the unit disc, while the point \((-3+\sqrt 8)i\) lies inside the unit disc. Thus
\begin{align*} \int _0^{2\pi } \frac {d\theta }{3+\sin \theta } &=\oint _\gamma f =2\pi i \Res _f(i(\sqrt {8}-3)) \\&= 2\pi i \lim _{z\to i(\sqrt 8-3)} (z-i(\sqrt 8-3)) f(z) \\&= 2\pi i \lim _{z\to i(\sqrt 8-3)} (z-i(\sqrt 8-3)) \frac {2}{z^2+6iz-1} \\&= 2\pi i \lim _{z\to i(\sqrt 8-3)} \frac {2(z-i(\sqrt 8-3)) }{(z-i(\sqrt 8-3))(z-(i(-\sqrt 8-3)))} \\&= 2\pi i \frac {2}{(i(\sqrt 8-3)-(i(-\sqrt 8-3)))} \\&= \frac {2\pi }{\sqrt 8} = \frac {\pi }{\sqrt 2} . \end{align*}
Let \(\cot z=\frac {\cos z}{\sin z}\). Show that \(\cot \) is holomorphic on \(\C \setminus \{n\pi :n\in \Z \}\), that \(\cot \) has a simple pole at \(n\pi \) for each \(n\in \Z \), and that \(\Res _{\cot {}}(n\pi )=1\) for all \(n\in \Z \).
Recall that \(\sin z= \frac {e^{iz}+e^{-iz}}{2i}\), while \(\cos z=\frac {e^{iz}+e^{-iz}}{2}\). Thus, \(\cot z=i\frac {e^{iz}+e^{-iz}}{e^{iz}-e^{-iz}}\).If \(x\), \(y\in \R \), then
\begin{equation*}\cot (x+iy) =i\frac {e^{i(x+iy)}+e^{-i(x+iy)}}{e^{i(x+iy)}-e^{-i(x+iy)}} =i\frac {e^{ix-y}+e^{-ix+y}}{e^{ix-y}-e^{-ix+y}} .\end{equation*}The singularities occur when (and only when) the denominator equals zero, that is, when
\begin{equation*}e^{ix-y}=e^{-ix+y}.\end{equation*}Recall that \(e^{ix-y}=e^{ix}e^{-y}=(\cos x+i\sin x)e^{-y}\). Thus, singularities occur when
\begin{equation*}(\cos x+i\sin x)e^{-y}=(\cos (-x)+i\sin (-x))e^y.\end{equation*}Because \(\cos \) is an even function and \(\sin \) is an odd function, singularities occur precisely when
\begin{equation*}(\cos x+i\sin x)e^{-y}=(\cos x-i\sin x)e^y.\end{equation*}Taking the real and imaginary parts of this equation, we see that \(\cot \) has a pole at \(x+iy\) if and only if
\begin{equation*}e^{-y}\cos x=e^y\cos x\quad \text {and}\quad e^{-y}\sin x = -e^y\sin x.\end{equation*}Considering the second equation, we can solve to see
\begin{equation*}(e^y+e^{-y})\sin x=0.\end{equation*}Since \(e^y+e^{-y}>0\) for all real numbers \(y\), we see that \(\sin x=0\), so \(x=n\pi \) for some \(n\in \Z \).
Considering the second equation, we see that \(\cos x=\pm 1\). In particular, \(\cos x\neq 0\), so \(e^{-y}=e^y\). This is true only for \(y=0\).
Thus, \(\cot z\) has singularities only at \(z=n\pi \) for \(n\in \Z \).
Now, choose some \(n\in \Z \). By l’Hôpital’s rule,
\begin{align*} \lim _{z\to n\pi } (z-n\pi )\cot z &=\lim _{z\to n\pi } \frac {(z-n\pi )\cos z}{\sin z} \\&=\lim _{z\to n\pi } \frac {\cos z-(z-n\pi )\sin z}{\cos z} =1 \end{align*}because \(\sin (n\pi )=0\) and \(\cos (n\pi )=\pm 1\neq 0\) for all \(n\in \Z \). This is a nonzero finite complex number and so \(\cot \) must have a simple pole at \(z=n\pi \). Furthermore, \(\Res _{\cot }(n\pi )=1\) for all \(n\in \Z \).
Show that \(\cot (x+iy)\) converges to \(-i\) as \(y\to \infty \) and to \(i\) as \(y\to -\infty \), uniformly in \(x\in \R \).
If \(x\), \(y\in \R \), then\begin{align*} \cot (x+iy)+i&= i\frac {e^{ix-y}+e^{-ix+y}}{e^{ix-y}-e^{-ix+y}} +i \\&=i\frac {e^{ix}e^{-y}+e^{-ix}e^{y}}{e^{ix}e^{-y}-e^{-ix}e^{y}} +i \\&=i\frac {2e^{ix}e^{-y}}{e^{ix}e^{-y}-e^{-ix}e^{y}} .\end{align*}By the reverse triangle inequality \(|e^{ix}e^{-y}-e^{-ix}e^{y}|\geq |e^{-ix}e^{y}|-|e^{ix}e^{-y}|=e^y-e^{-y}\). Thus, for all \(x\in \R \) and all \(y>0\) we have that
\begin{align*} |\cot (x+iy)+i|&\leq \frac {2e^{-y}}{e^{y}-e^{-y}} =\frac {2}{e^{2y}-1} .\end{align*}We know from real analysis that \(\lim _{y\to \infty } \frac {2}{e^{2y}-1}=0\), that is, for every \(\varepsilon >0\) there is a \(N\in \R \) such that if \(y>0\) then \(\frac {2}{e^{2y}-1}<\varepsilon \). Thus, if \(y>N\), then for all \(x\in \R \) we have that \(|\cot (x+iy)+i|<\varepsilon \), and so \(\cot (x+iy)\to -i\) as \(y\to \infty \) uniformly in \(x\). A similar argument yields the limit as \(y\to -\infty \).
Show that if \(x=(k+1/2)\pi \) for some \(k\in \Z \), then \(|\cot (x+iy)|<1\) for all \(y\in \R \).
Recall\begin{equation*}\cot (x+iy)=i\frac {e^{ix-y}+e^{-ix+y}}{e^{ix-y}-e^{-ix+y}} =i\frac {e^{ix}e^{-y}+e^{-ix}e^{y}}{e^{ix}e^{-y}-e^{-ix}e^{y}} .\end{equation*}Multiplying on the top and bottom by \(e^{ix}\), we see that
\begin{equation*}\cot (x+iy) =i\frac {e^{2ix}e^{-y}+e^{y}}{e^{2ix}e^{-y}-e^{y}} .\end{equation*}If \(x=(k\pi +\pi /2)\), then \(2x=2k\pi +\pi \) and so \(e^{2ix}=e^{2k\pi i+\pi i}=-1\). Thus
\begin{equation*} \cot ((k+1/2)\pi +iy) =i\frac {-e^{-y}+e^{y}}{-e^{-y}-e^{y}} .\end{equation*}Note that \(e^{-y}-e^y\) is a real number with \(|e^{-y}-e^y|< e^{-y}+e^y\), and so
\begin{equation*}|\cot ((n+1/2)\pi +iy)| =\frac {|e^{-y}-e^{y}|}{e^{-y}+e^{y}} < 1.\end{equation*}
In the remainder of this section we will compute \(\sum _{n=1}^\infty \frac {1}{n^2}\). We now begin the computation. Let \(\gamma _k:[0,1]\to \C \) be a \(C^1\) parameterization of the rectangle with corners at \(\pm (k\pi +\frac {\pi }{2})\pm ik\), for \(k\in \N \). Let \(f(z)=\frac {\cot z}{z^2}\). Show that \(\lim _{k\to \infty } \oint _{\gamma _k} f=0\).
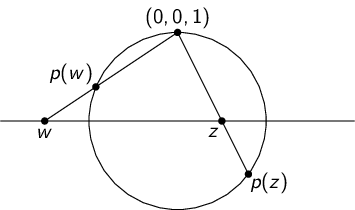
\usepackage{tikz} ... \begin{tikzpicture} \draw (-5,-2) node [below left] {$-k\pi-\frac{\pi}{2}-ik$} -- node [below] {$\psi_k$} (5,-2) node [below right] {$k\pi+\frac{\pi}{2}-ik$} -- node [right] {$\varphi_k$} (5,2) node [above right] {$k\pi+\frac{\pi}{2}+ik$} -- node [above] {$\eta_k$} (-5,2) node [above left] {$k\pi+\frac{\pi}{2}+ik$} -- node [left] {$\theta_k$} cycle ; \end{tikzpicture}Let \(\psi _k\), \(\varphi _k\), \(\eta _k\), and \(\theta _k\) be the four indicated straight-line contours; observe that we may combine these four contours to the contour \(\gamma _k\) using 1050Problem 1050. Then
\begin{equation*}\oint _{\gamma _k}f = \oint _{\psi _k}f + \oint _{\varphi _k}f + \oint _{\eta _k}f + \oint _{\theta _k}f.\end{equation*}By Proposition 2.1.8, we have that
\begin{equation*}\biggl |\oint _{\psi _k}f| \leq \ell (\psi _k)\sup _{\widetilde {\psi _k}} |f| \leq (2k\pi +\pi ) \frac {1}{k^2}\sup _{x\in \R } |\cot (x-ik)|.\end{equation*}But by 2740Problem 2740 \(\cot (x+iy)\to i\) as \(y\to -\infty \), uniformly in \(x\); thus if \(k\) is sufficiently large then \(|\cot (x-ik)-i|<1\) and so \(|\cot (x-ik)|<1+|i|=2\) for all \(x\in \R \). Thus
\begin{equation*}\biggl |\oint _{\psi _k}f| \leq \frac {4k\pi +2\pi }{k^2}\end{equation*}whenever \(k\) is large enough, and so \(\lim _{k\to \infty } \oint _{\psi _k}f=0\). Similarly \(\lim _{k\to \infty } \oint _{\eta _k}f=0\).
Again by Proposition 2.1.8, we have that
\begin{equation*}\biggl |\oint _{\varphi _k}f| \leq \ell (\varphi _k)\sup _{\widetilde {\varphi _k}} |f| \leq (2k) \frac {1}{k^2}\sup _{y\in \R } |\cot (k\pi +\pi /2+iy)|\end{equation*}which by 2750Problem 2750 is at most \(\frac {2k}{k^2}\). Thus \(\lim _{k\to \infty } \oint _{\varphi _k}f=0\). Similarly \(\lim _{k\to \infty } \oint _{\theta _k}f=0\) and the proof is complete.
Find the residue of \(f\) at zero.
First observe that\begin{align*} \lim _{z\to 0} z^3f(z)&=\lim _{z\to 0} z\cot z=\lim _{z\to 0} \frac {z\cos z}{\sin z} \\&=\lim _{z\to 0}\frac {\cos z-z\sin z}{\cos z} = 1 \end{align*}by l’Hôpital’s rule. This is a nonzero finite complex number, so \(f\) must have a pole of order \(3\) at \(0\).
We write the Laurent series of \(f\) about \(z=0\) as
\begin{equation*}f(z)=\sum _{k=-3}^\infty a_kz^k.\end{equation*}Note that \(a_{-3}=1\). Thus
\begin{equation*}f(z)-\frac {1}{z^3}=\sum _{k=-2}^\infty a_k z^k\end{equation*}and
\begin{align*}a_{-2} &=\lim _{z\to 0}\sum _{k=-2}^\infty a_k z^{k+2} =\lim _{z\to 0}z^2\sum _{k=-2}^\infty a_k z^{k} \\&=\lim _{z\to 0} z^2\left (f(z)-\frac {1}{z^3}\right ) = \lim _{z\to 0} \cot z-\frac {1}{z} \\&=\lim _{z\to 0} \frac {z\cos z-\sin z}{z\sin z} =\lim _{z\to 0} \frac {-z\sin z}{\sin z+z\cos z} \\&=\lim _{z\to 0} \frac {-\sin x-z\cos z}{2\cos z-z\sin z}=0. \end{align*}Thus,
\begin{align*} \Res _f(0)=a_{-1} &=\lim _{z\to 0} z\left (f(z)-\frac {1}{z^3}-\frac {0}{z^2}\right ) =\lim _{z\to 0} \frac {\cot z}{z}-\frac {1}{z^2} \\&=\lim _{z\to 0} \frac {z\cot z-1}{z^2} =\lim _{z\to 0} \frac {z\cos z-\sin z}{z^2\sin z} \end{align*}and repeated applications of l’Hôpital’s rule yield that
\begin{align*} \Res _f(0)&=\lim _{z\to 0} \frac {-z\sin z}{2z\sin z+z^2\cos z} \\&=\lim _{z\to 0} \frac {-\sin z-z\cos z}{2\sin z+4\,z\cos z-z^2\sin z} \\&=\lim _{z\to 0} \frac {-2\cos z+z\sin z}{6\cos z-6\,z\sin z-z^2\cos z} =-\frac {1}{3}. \end{align*}
Find all the remaining singularities of \(f\) and then find the residues of \(f\) at each such singularity.
By 2730Problem 2730 we have that \(\cot \) is holomorphic on \(\C \setminus \{n\pi :n\in \Z \}\). The function \(g(z)=\frac {1}{z^2}\) is holomorphic on \(\C \setminus \{0\}\), and so the function \(f\) must also be holomorphic on \(\C \setminus \{n\pi :n\in \Z \}\).We thus need only find \(\Res _{f}(n\pi )\) for \(n\in \Z \), \(n\neq 0\).
If \(n\neq 0\) then \(\lim _{z\to n\pi } \frac {1}{z^2}=\frac {1}{n^2\pi ^2}\). By 2730Problem 2730 \(\cot \) has a simple pole at \(n\pi \) and has residue \(1\), and so \(\lim _{z\to n\pi } (z-n\pi )\cot (z)=1\). Thus
\begin{equation*}\frac {1}{n^2\pi ^2} = \Bigl (\lim _{z\to n\pi } \frac {1}{z^2}\Bigr )\Bigl (\lim _{z\to n\pi } (z-n\pi )\cot (z)\Bigr ).\end{equation*}Because both limits exist the limit of the product is the product of the limits, and so
\begin{equation*}\frac {1}{n^2\pi ^2}=\lim _{z\to n\pi } \frac {1}{z^2}(z-n\pi )\cot z = \lim _{z\to n\pi } (z-n\pi )f(z) .\end{equation*}Thus \(f\) has a simple pole at \(n\pi \) for each \(n\in \Z \setminus \{0\}\) and \(\Res _f(n\pi )=\frac {1}{n^2\pi ^2}\).
Use the above results to compute \(\sum _{n=1}^\infty \frac {1}{n^2}\).
By Theorem 4.5.3, and because the singular set for \(f\) is \(\{n\pi :n\in \Z \}\), we have that\begin{equation*}\oint _{\gamma _k} f = 2\pi i\Bigl (\sum _{n=-k}^k \Res _f(\pi n)\Bigr ).\end{equation*}But \(\lim _{k\to \infty } \oint _{\gamma _k} f=0\) by 2760Problem 2760, and so we must have that
\begin{equation*}0=\lim _{k\to \infty } \sum _{n=-k}^k \Res _f(\pi n).\end{equation*}Rewriting the right hand side we see that
\begin{align*} 0&=\Res _f(0)+\lim _{k\to \infty } \sum _{n=1}^k (\Res _f(\pi n)+\Res _f(-\pi n)) =\Res _f(0)+\sum _{n=1}^\infty (\Res _f(\pi n)+\Res _f(-\pi n)) .\end{align*}By 2780Problem 2780 and 2770Problem 2770,
\begin{equation*}0=-\frac {1}{3}+\sum _{n=1}^\infty \frac {1}{(n\pi )^2}+\frac {1}{(-n\pi )^2} .\end{equation*}Simple algebra yields that
\begin{equation*}\sum _{n=1}^\infty \frac {1}{(n\pi )^2}=\frac {\pi ^2}{6}.\end{equation*}
Let \(\Omega \subseteq \C \) be open. A function \(f\) is said to be meromorphic on \(\Omega \) if there is a set \(S\) such that
We call \(S\) the singular set for \(f\).3
Let \(\Omega \) be a connected open set and let \(f:\Omega \to \C \) be holomorphic and not constant. Then the set \(S=\{z\in \Omega :f(z)=0\}\subset \Omega \) has no accumulation points in \(\Omega \).
Let \(\Omega \subseteq \C \) be open and let \(S\subset \Omega \) have no accumulation points in \(\Omega \). Show that \(\Omega \setminus S\) is both open and dense in \(\Omega \).
Let \(z\in \Omega \). Then there is an \(r>0\) such that \(D(z,r)\subseteq \Omega \).\(z\) is not an accumulation point for \(S\), and so there is an \(\varepsilon >0\) such that \(D(z,\varepsilon )\setminus \{z\}\) contains no points of \(S\).
Let \(\varrho =\min (r,\varepsilon )\); since \(r>0\) and \(\varepsilon >0\) we have that \(\varrho >0\) as well.
If \(z\in \Omega \setminus S\) then \(D(z,\varrho )\subset \Omega \setminus S\) and \(\varrho >0\). This is true for all \(z\in \Omega \setminus S\), and so \(\Omega \setminus S\) is open.
If \(z\in \Omega \), let \(\delta >0\). Then \(D(z,\min (\delta ,\varrho ))\setminus \{z\}\) is not empty because \(\min (\delta ,\varrho )>0\) and it lies entirely within \(\Omega \setminus S\); thus, in particular \(D(z,\delta )\) contains at least one point of \(\Omega \setminus S\) (all of the points in \(D(z,\min (\delta ,\varrho ))\setminus \{z\}\)), and so \(\Omega \setminus S\) is dense in \(\Omega \).
Let \(K\subset \Omega \) be compact. Then \(K\cap S\) is finite.
Suppose in addition that \(\Omega \) is connected. Show that \(\Omega \setminus S\) is connected.
Recall that any connected open set in \(\R ^2=\C \) is path connected. Let \(z\), \(w\in \Omega \setminus S\) and let \(\gamma :[0,1]\to \Omega \) be continuous with \(\gamma (0)=z\) and \(\gamma (1)=w\).We may assume that \(\gamma \) is one-to-one. Because \(\gamma \) is continuous and \([0,1]\) is compact, we have that \(\gamma ([0,1])\) is compact, and so by Problem 3.42 we have that \(\gamma ([0,1])\) contains at most finitely many points of \(S\).
Define \(\psi \) as follows. Let \(\{t_1,t_2,\dots ,t_n\}=\gamma ^{-1}(S)\). For each \(k\) there is an \(r_k>0\) such that \(D(\gamma (t_k),r_k)\subset \Omega \) and \(D(\gamma (t_k),r_k)\cap S=\{\gamma (t_k)\}\).
Let \(\varepsilon >0\) be such that \(\varepsilon <r_k\) and also \(\varepsilon <|t_k-t_\ell |\) for all \(k\) and \(\ell \). Because \(\gamma \) is one-to-one and there are at most finitely many \(t_k\)s, we may find such a positive \(\varepsilon >0\). Because \(\gamma \) is continuous on a connected set, it is uniformly continuous; let \(\delta >0\) be such that if \(|t-s|<\delta \) then \(|\gamma (t)-\gamma (s)|<\varepsilon /4\).
We may then let \(\psi (t)=\gamma (t)\) if \(t\notin \bigcup _k (t_k-\delta ,t_k+\delta )\), and define \(\psi \) such that \(\psi (t)\in D(\gamma (t_k),\varepsilon /3)\) for all \(t\in (t_k-\delta ,t_k+\delta )\) but such that \(\psi (t)\neq \psi (t_k)\). In particular \(\psi (t)\notin S\) and \(\psi (t)\in \Omega \) for all \(t\in (t_k-\delta ,t_k+\delta )\), and thus for all \(t\in [0,1]\).
Then \(\psi \) is a continuous path in \(\Omega \setminus S\) from \(z\) to \(w\). Because \(z\) and \(w\) were arbitrary this implies that \(\Omega \setminus S\) is path connected, and therefore connected.
If \(\Omega \subseteq \C \) is open, and if \(S\) and \(Z\) are two subsets of \(\Omega \) with no accumulation points in \(\Omega \), show that \(S\cup Z\) has no accumulation points in \(\Omega \).
In particular, let \(f\) be meromorphic and non-constant in \(\Omega \) for some \(\Omega \subseteq \C \) open and connected. Let \(S\) be the singular set for \(f\) and let \(Z=\{z\in \Omega \setminus S:f(z)=0\}\) be the zero set. Show that \(S\cup Z\) has no accumulation points in \(\Omega \).
Let \(z\in \Omega \). \(z\) is not an accumulation point for \(S\), and so there is a \(r_S>0\) such that \(S\cap D(z,r_S)\setminus \{z\}=\emptyset \). Similarly, there is a \(r_Z>0\) such that \(Z\cap D(z,r_Z)\setminus \{z\}=\emptyset \). Letting \(r=\min (r_S,r_Z)\), we see that \(r>0\) and that \((S\cup Z)\cap D(z,r)\setminus \{z\}=\emptyset \), as desired.
The sum of two meromorphic functions is meromorphic.
The product of two meromorphic functions is meromorphic.
Show that the derivative of a meromorphic function is meromorphic.
Let \(S\) be the singular set for \(\Omega \); by definition of meromorphic \(S\subset \Omega \) and \(S\) has no accumulation points in \(\Omega \). Then \(f\) is holomorphic in \(\Omega \setminus S\). \(\Omega \setminus S\) is open by 2870Problem 2870, and so by Corollary 3.1.2 \(f'\) is also holomorphic in \(\Omega \setminus S\).We need only show that, if \(s\in S\), then \(f'\) has a pole at \(s\). Because \(\Omega \) is open and the points of \(S\) are isolated, if \(s\in S\) then there is a \(r>0\) such that \(D(s,r)\subset \Omega \) and \(D(s,r)\cap S=\{s\}\). Therefore \(f\) has a Laurent series in \(D(s,r)\setminus \{s\}\). By assumption \(f\) has a pole at \(S\), and so by 2300Problem 2300 there is a \(n>0\) such that \(a_{-n}\neq 0\) and such that
\begin{equation*}f(z)=\sum _{k=-n}^\infty a_k(z-s)^k\end{equation*}for all \(z\in D(s,r)\setminus \{s\}\).
By Proposition 4.3.3 and Corollary 3.5.2, if \(z\in D(s,r)\setminus \{s\}\) then
\begin{equation*}f'(z)=\sum _{k=-n}^\infty ka_k(z-s)^{k-1} =\sum _{j=-n-1}^\infty (j+1)a_{j+1}(z-s)^{j}\end{equation*}and so by 2310Problem 2310 \(f'\) has a pole at \(s\).
Suppose that \(f\) is meromorphic in \(\Omega \). Then the function obtained by extending \(1/f\) as much as possible using the Riemann removable singularities theorem is meromorphic in \(\Omega \).
Suppose that \(\Omega \), \(W\subseteq \C \) are open and connected, that \(f:\Omega \to W\) is holomorphic and not constant, and that \(S\subset W\) has no accumulation points in \(W\). Show that \(f^{-1}(S)\) has no accumulation points in \(\Omega \).
Suppose not. Let \(T=f^{-1}(S)\) and let \(\zeta \in \Omega \). Then \(f(\zeta )\in W\) and so \(f(\zeta )\) is not an accumulation point of \(S\). There is thus a \(\varepsilon >0\) such that \(D(f(\zeta ),\varepsilon )\cap S\subseteq \{f(\zeta )\}\) (that is, the intersection is either empty or the single point \(f(z)\)).Suppose that \(\zeta \) is an accumulation point for \(T\). Let \(\{s_k\}_{k=1}^\infty \) be a sequence of distinct points in \(T\) with \(s_k\to \zeta \). Then by continuity of \(f\) we have that \(f(s_k)\to f(\zeta )\in W\). Thus, there is a \(N\in \N \) such that if \(k>N\) then \(f(s_k)\in D(f(\zeta ),\varepsilon )\).
By definition of \(T\), \(f(s_k)\in S\) for all \(k\). Thus if \(k>N\) then \(f(s_k)\in D(f(\zeta ),\varepsilon )\cap T\subseteq \{f(\zeta )\}\), and so we must have \(f(s_k)=f(\zeta )\) for all \(k>N\). Thus \(\{z\in \Omega :f(z)=f(\zeta )\}\) has an accumulation point, namely \(\zeta \); by Theorem 3.6.1 \(f\) is a constant, contradicting our assumption.
Thus \(T\subset \Omega \) has no accumulation points in \(\Omega \).
Suppose that \(\Omega \), \(W\subseteq \C \) are open and connected, that \(f:\Omega \to W\) is holomorphic and not constant, and that \(g:W\to \C \) is meromorphic in \(W\). Show that \(g\circ f\) is meromorphic in \(\Omega \).
Let \(S_g\subset W\) be the singular set for \(g\). Let \(S=f^{-1}(S_g)=\{z\in \Omega :f(z)\in S_g\}\). By the previous problem \(S\) has no accumulation points in \(\Omega \).By Problem 1.49 in your book, \(g\circ f\) is holomorphic in \(\Omega \setminus S\).
Now, let \(s\in S\). We need only show that \(g\circ f\) has a pole at \(s\).
Because \(s\) is not an accumulation point of \(S\) there is a \(r>0\) such that \(D(s,r)\cap S=\{s\}\).
We know that \(f(s)\in S_g\), and so \(g\) has a pole at \(f(s)\). Thus \(\lim _{w\to f(s)}|g(w)|=\infty \): for any \(N\in \R \) there is a \(\varepsilon >0\) such that if \(0<|w-f(s)|<\varepsilon \) then \(|g(w)|>N\). But \(f\) is continuous at \(s\), and so there is a \(\delta >0\) such that if \(|z-s|<\delta \) then \(|f(z)-f(s)|<\varepsilon \).
Thus if \(0<|z-s|<\min (\delta ,r)\) then \(z\notin S\) and so \(f(z)\notin S_g\), and so \(f(z)\neq f(s)\in S_g\). Thus \(0<|f(z)-f(s)|<\varepsilon \) and so \(|g(f(z))|>N\), as desired.
Let \(X=\C \cup \{\infty \}\) (where \(\infty \) is a single point not in \(\C \)) and define \(d:X\times X\to [0,\infty )\) by
This is called the spherical metric on \(X\). Then \((X,d)\) is a metric space. (See Problem 4.32 in your book.)
This metric arises as follows. If \(z=\xi +i\eta \), where \(\xi \), \(\eta \in \R \), then we let the stereographic projection \(p(z)\) be the point in \(\R ^3\) that lies on the unit sphere \(\{(x,y,t):x^2+y^2+t^2=1\}\) and also lies on the line through \((0,0,1)\) (the north pole) and the point \((\xi ,\eta ,0)\). See the following figure. Then \(d(z,w)=\|p(z)-p(w)\|\) (if \(z\), \(w\in \C \) and \(\|\,\cdot \,\|\) denotes the standard Euclidean metric in \(\R ^3\)) and \(d(z,\infty )=\|(0,0,1)-p(z)\|\).
The subspace \((\C ,d)\) is equivalent to \((\C ,|\cdot -\cdot |)\) (that is, \(\C \) equipped with the standard metric) in the sense that, if \(x\), \(x_n\in \C \), then \(x_n\to x\) in \((\C ,d)\) if and only if \(x_n\to x\) in \((\C ,|\cdot -\cdot |)\).
The subspace \((\C ,d)\) is equivalent to \((\C ,|\cdot -\cdot |)\) in the sense that if \(z\in \Omega \subseteq \C \) and \(f\) is a function defined on \(\Omega \), then \(f\) is continuous at \(z\) as a function on \((\Omega ,d)\) if and only if \(f\) is continuous at \(z\) as a function on \((\Omega ,|\cdot -\cdot |)\).
The subspace \((\C ,d)\) is equivalent to \((\C ,|\cdot -\cdot |)\) in the sense that if \(f:Y\to \C \) is a function defined on a metric space \(Y\) and \(a\in Y\), then \(f\) is continuous at \(a\) as a function mapping into \((X,d)\) (or \((\C ,d)\)) if and only if \(f\) is continuous at \(a\) as a function mapping into \((\C ,|\cdot -\cdot |)\).
If \(\{x_n\}_{n=1}^\infty \subset \C \), then \(x_n\to \infty \) in \((X,d)\) if and only if \(\lim _{n\to \infty } |x_n|=\infty \) in the sense of real analysis.
If \(\Omega \subseteq \C \) is unbounded and \(f:\Omega \to Y\) for some metric space \((Y,\rho )\), we may define \(\lim _{z\to \infty } f(z)\) in \((\C ,|\cdot -\cdot |)\) as follows: \(\lim _{z\to \infty } f(z)=L\) if, for every \(\varepsilon >0\), there is a \(N>0\) such that if \(z\in \Omega \) and \(|z|>N\), then \(\rho (f(z),L)<\varepsilon \). Show that \(\lim _{z\to \infty } f(z)=L\) in \((\C ,|\cdot -\cdot |)\) if and only if \(\lim _{z\to \infty } f(z)=L\) in \((X,d)\).
If \((Y,\rho )\) is a metric space, \(a\in Y\), and \(f:Y\setminus \{a\}\to C\), then we say that \(\lim _{y\to a} f(y)=\infty \) in \((\C ,|\cdot -\cdot |)\) if for every \(R>0\) there is a \(\delta >0\) such that if \(0<\rho (a,y)<\delta \) then \(|f(y)|>R\). Show that \(\lim _{y\to a} f(y)=\infty \) in \((\C ,|\cdot -\cdot |)\) if and only if \(\lim _{y\to a} f(y)=\infty \) in \((X,d)\).
Suppose that \(\Omega \subseteq \C \) is open and that \(S\subset \Omega \) has no accumulation points in \(\Omega \). Show that \(f\) is meromorphic in \(\Omega \) with singular set \(S\) if and only if \(f\) is holomorphic in \(\Omega \setminus S\) and if the function \(\hat f\) given by
is continuous as a function from \(\Omega \) to \((X,d)\), where \((X,d)\) is the metric space in 2930Problem 2930.
Let \(\Omega \subseteq \C \) be open. Suppose that there is some \(R>0\) such that
If \(f\) is holomorphic on \(\Omega \), then we say that \(f\) has an isolated singularity at \(\infty \).
Let \(W=\{z\in \C \setminus \{0\}:1/z\in \Omega \}\) and define \(g:W\to \C \) by \(g(z)=f(1/z)\).
If \(f\) has a removable singularity or pole at \(\infty \), we say that \(f\) is meromorphic at \(\infty \).
If \(f\) is holomorphic on an open set \(\Omega \), and \(\Omega \supseteq D(0,\infty )\setminus \overline D(0,R)=\{z\in \C :|z|>R\}\), then there is a unique Laurent series \(\sum _{n=-\infty }^\infty a_n z^n\) that converges to \(f\) on \(\{z\in \C :|z|>R\}\).
If there is an \(R>0\) such that \(\sum _{n=-\infty }^\infty a_n z^n\) that converges to \(f\) on \(\{z\in \C :|z|>R\}\), then we call \(\sum _{n=-\infty }^\infty a_n z^n\) the Laurent expansion of \(f\) around \(\infty \).
Let \(f\) have an isolated singularity at \(\infty \).
If \(f\) has an isolated singularity at \(\infty \), and the Laurent expansion of \(f\) about \(\infty \) is \(f(z)=\sum _{n=-\infty }^\infty a_nz^n\) for all \(|z|>R\), then the rows in this table all contain three equivalent statements.
\(f\) has a removable singularity at \(\infty \)
\(\displaystyle \limsup _{z\to \infty } |f(z)|<\infty \) (this means that there is a \(r>0\) such that \(\sup _{|z|>r} |f(z)|<\infty \)). Alternatively, \(\displaystyle \lim _{z\to \infty } f(z)=L\) for some \(L\in \C \).
\(a_n=0\) for all \(n>0\)
\(f\) has a pole at \(\infty \)
\(\displaystyle \lim _{z\to \infty }|f(z)|=\infty \)
There is a \(n\in \N \) (with \(n>0\)) such that \(a_n\neq 0\) and \(a_k=0\) for all \(k>n\)
\(f\) has an essential singularity at \(\infty \)
\(\displaystyle \limsup _{z\to \infty } |f(z)|=\infty \) and \(\displaystyle \liminf _{z\to \infty } |f(z)|=0\) (or \(\displaystyle \limsup _{z\to \infty } |f(z)|\neq \liminf _{z\to \infty } |f(z)|\))
If \(n\in \N \) then there is a \(k\in \N \) with \(k>n\) and \(a_k\neq 0\)
Let \(\Omega \), \(W\subset \C \) be open. Suppose that \(f\) is meromorphic and not constant in \(\Omega \) and that \(g\) is meromorphic in \(W\). If \(f\) has any poles, we require that \(g\) be meromorphic at \(\infty \); that is, there is an \(R>0\) such that\(\{z\in \C :|z|>R\}\subseteq W\) and \(g\) has no poles in \(\{z\in \C :|z|>R\}\), and furthermore that \(g\) has either a removable singularity or a pole at \(\infty \). Suppose furthermore that \(f(\Omega \setminus S_f)\subseteq W\) where \(S_f\) is the singular set for \(f\). Show that \(g\circ f\) is meromorphic on \(\Omega \) (possibly after “filling in” removable singularities).
Suppose that \(\Omega \subseteq \C \) is open and that \(S\subset \Omega \) has no accumulation points in \(\Omega \). Further suppose that there is some \(R>0\) such that \(\{z\in \C :|z|>R\}\subseteq \Omega \setminus S\). Show that \(f\) is meromorphic in \(\Omega \) and at \(\infty \) with singular set \(S\) if and only if \(f\) is holomorphic in \(\Omega \setminus S\) and if the function \(\hat f\) given by
is continuous as a function from \(\Omega \cup \{\infty \}\subseteq X\) (with the metric \(d\)) to \((X,d)\), where \((X,d)\) is the metric space in 2930Problem 2930.
Suppose that \(f:\C \to \C \) is entire and is also meromorphic at \(\infty \). Then \(f\) is a polynomial.
Prove Theorem 4.7.5.
Because \(f\) is entire, \(f\) has a power series\begin{equation*}f(z)=\sum _{n=0}^\infty a_n z^n\end{equation*}for all \(z\in \C \). This is then the Laurent expansion about \(\infty \) of \(f\), and so by 3010Problem 3010 we have that there is a \(N\in \N _0\) such that \(a_n=0\) for all \(n>N\). Thus
\begin{equation*}f(z)=\sum _{n=0}^N a_n z^n\end{equation*}and so \(f\) is a polynomial.
Suppose that \(f\) is meromorphic in \(\C \) and also is meromorphic at \(\infty \). Then there are two polynomials \(p\) and \(q\) such that the singular set of \(f\) is equal to the zero set of \(q\) and such that \(f(z)=\frac {p(z)}{q(z)}\) for all \(z\) in \(\C \) outside of the singular set.
Prove Theorem 4.7.7.
Because \(f\) is meromorphic at \(\infty \), we have that \(f\) has an isolated singularity at \(\infty \); that is, there is a \(R>0\) such that if \(S\) is the singular set for \(f\) then \(S\cap \{z\in \C :|z|>R\}=\emptyset \).Thus \(S\subset \overline D(0,R)\). \(\overline D(0,R)\) is compact and \(S\) has no accumulation points, so by Problem 3.42 \(\overline D(0,R)\) contains only finitely many points of \(S\). But \(\overline D(0,R)\) contains all points of \(S\), so \(S\) is finite. Let \(S=\{s_1,s_2,\dots ,s_m\}\).
Let \(n_k\) be the order of the pole of \(f\) at \(s_k\). Then \(q(z)=\prod _{k=1}^m (z-s_k)^{n_k}\) is a polynomial. By 2330Problem 2330 and 2340Problem 2340, \(q(z)f(z)\) has removable singularities at each \(s_k\). We may extend \(qf\) using the Riemann removable singularities theorem to an entire function \(p\).
The function \(f\) has a Laurent expansion \(\sum _{k=-\infty }^n a_kz^k\) about \(\infty \); because \(f\) is meromorphic at \(\infty \), we have that \(n<\infty \). Multiplying by a polynomial yields that the Laurent expansion of \(p\) about \(\infty \) is \(\sum _{k=-\infty }^{n+m} b_kz^k\) where \(m\) is the degree of the polynomial \(q(z)\); thus \(p\) is also meromorphic at \(\infty \).
Because \(p\) is meromorphic at \(\infty \) and also entire, \(p\) is a polynomial by Theorem 4.7.5. Then
\begin{equation*}f(z)=\frac {p(z)}{q(z)}\end{equation*}where \(p\) and \(q\) are polynomials, as desired.
(Argument principle for meromorphic functions.) Let \(\Omega \subseteq \C \) be open and let \(f\) be meromorphic in \(\Omega \). Let \(\overline D(P,r)\subset \Omega \). Suppose that \(f\) has no poles on \(\partial D(P,r)\) and that \(f(z)\neq 0\) for all \(z\in \partial D(P,r)\). Then
where \(n_1,\dots n_p\) are the multiplicities of the zeroes \(z_1,\dots ,z_p\) of \(f\) in \(D(P,r)\) and where \(m_1,\dots m_q\) are the orders of the poles \(w_1,\dots ,w_q\) of \(f\) in \(D(P,r)\).
Suppose that \(\Omega \subseteq \C \) is open, \(f\) is meromorphic in \(\Omega \), and \(\overline D(P,r)\subset \Omega \). Then \(f\) has at most finitely many poles and at most finitely many zeroes in \(\overline D(P,r)\).
Prove Theorem 5.1.4. Here is a suggested approach. Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be meromorphic and not uniformly zero. Let \(g(z)=\frac {f'(z)}{f(z)}\); then \(g\) is meromorphic in \(\Omega \).
Suppose that \(f\) has a zero or pole at \(\zeta \). Let \(n\) be the order of the zero or the negative of the order of the pole; then \((z-\zeta )^{-n}f(z)\) has a removable singularity at \(\zeta \) and \(\lim _{z\to \zeta } f(z)\neq 0\). Let \(h(z)\) be the extension of \((z-\zeta )^{-n}f(z)\) given by the Riemann removable singularities theorem.
Then \(f(z)=(z-\zeta )^nh(z)\) in a punctured neighborhood of \(\zeta \), and so
\begin{equation*}\frac {f'(z)}{f(z)} = \frac {n(z-\zeta )^{n-1}h(z)+(z-\zeta )^nh'(z)}{(z-\zeta )^{n}h(z)} = \frac {n}{z-\zeta }+\frac {h'(z)}{h(z)}.\end{equation*}But \(h(\zeta )\neq 0\) and \(h\) is continuous, so \(h\neq 0\) in a neighborhood of \(\zeta \) and so \(h'/h\) is holomorphic in that neighborhood. Thus \(\Res _{f'/f}(\zeta )=n+\Res _{h'/h}(\zeta )=n\).
The conclusion follows from the residue theorem (Theorem 4.5.3).
Write down a version of the argument principle that allows us to count the number of solutions to \(f(z)=3\) in \(D(P,r)\).
If \(\gamma \) is a \(C^1\) curve and \(f\) is holomorphic in a neighborhood of \(\widetilde \gamma \) then \(f\circ \gamma \) is also a \(C^1\) curve. Clearly, if \(\gamma \) is closed then so is \(f\circ \gamma \).
Suppose that \(\gamma \) is the standard counterclockwise parameterization of \(\partial D(P,r)\), that \(f\) is holomorphic in \(D(P,R)\) for some \(R>r\), and that \(f(\partial D(P,r))\subset \C \setminus \{0\}\). Show that \(\Ind _{f\circ \gamma }(0)\) is equal to the number of solutions to \(f(z)=0\) in \(D(P,r)\) (counted with multiplicity). Hint: Use the argument principle.
Recall that, if \(\eta \) is a closed path and \(w\in \C \setminus \widetilde \eta \), then \(\Ind _\eta (w)\) is defined to be\begin{equation*}\Ind _\eta (w)=\frac {1}{2\pi i} \oint _\eta \frac {1}{\zeta -w}\,d\zeta .\end{equation*}Thus
\begin{equation*}\Ind _{f\circ \gamma }(0) =\frac {1}{2\pi i} \oint _{f\circ \gamma }\frac {1}{\zeta }\,d\zeta =\frac {1}{2\pi i} \oint _{f\circ \gamma }g \end{equation*}where \(g(z)=\frac {1}{z}\).
Because \(f\) is continuous and \(\partial D(P,r)\) is compact, we have that there exist \(r_1\), \(R_1\) with \(0<r_1<r<R_1<R\) such that \(f\) is nonzero on \(\Omega =D(P,R_1)\setminus \overline D(P,r_1)\), that is, \(f:\Omega \to W=\C \setminus \{0\}\). Observe that \(g\) is continuous on \(W\).
By our change of variable result 1060Problem 1060 with \(u\) replaced by \(f\) and \(f\) replaced by \(g\), we have that
\begin{equation*}\Ind _{f\circ \gamma }(0) =\frac {1}{2\pi i} \oint _{f\circ \gamma }g =\frac {1}{2\pi i}\oint _\gamma g\circ f\,f' =\frac {1}{2\pi i} \oint _\gamma \frac {f'}{f} .\end{equation*}The argument principle completes the proof.
You are given that \(f\) is holomorphic in \(D(0,2)\) and that there are at most finitely many points \(w\) such that \(f(z)=w\) for more than one \(z\in \partial D(0,1)\). Illustrated are the three points \(0\), \(-3\), and \(5\) and the set \(f(\partial D(0,1))\).
We must have that \(f(z)=-3\) has three solutions and \(f(z)=5\) has two solutions (counted with multiplicity). The multiplicity of the zero at \(0\) must be \(3\).
You are given that \(g\) is holomorphic in \(D(0,2)\). Illustrated is the point \(0\) and the set \(g(\partial D(0,1))\). You are given that there are four solutions to the equation \(g(z)=0\) in \(D(0,1)\). How is this possible?
The curve \(g\circ \gamma \), where \(\gamma :[0,2\pi ]\to \C \) and \(\gamma (t)=e^{it}\), must be \(2\)-to-1 at most points; that is, most points in \(g(\partial D(0,1))\) must have two preimages instead of one.
Let \(X\) be a compact metric space and let \(f:X\to Z\) be a continuous function. Then \(f(X)\) is compact.
Let \(K\subseteq \C \) be compact and let \(\Omega \subseteq \C \) be a connected component of \(\C \setminus K\). Then \(\Omega \) is open.
(The open mapping theorem.) Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic. Then either \(f(\Omega )=\{Q\}\) for some \(Q\in \C \) or \(f(\Omega )\) is an open subset of \(\C \).
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic and not constant. Let \(P\in \Omega \) and let \(Q=f(P)\). Then there is a \(r>0\) such that \(\overline D(P,r)\subset \Omega \) and such that \(f(\zeta )\neq Q\) for all \(\zeta \in \partial D(P,r)\).
[Redacted]
Prove the open mapping theorem. Hint: Assume \(f\) is not constant, \(P\in \Omega \), and \(Q=f(P)\). Let \(r>0\) be as in 2030Problem 2030. Consider \(\C \setminus f(\partial D(P,r))\) and use 880Memory 880, 3120Memory 3120, 3090Problem 3090, and 2540Problem 2540 to show that \(f(\Omega )\) contains an open neighborhood of \(Q\).
The set \(\partial D(P,r)\) is compact. By 880Memory 880 and 3120Memory 3120, the connected components of \(\C \setminus f(\partial D(P,r))\) are all open. By our choice of \(r\) (that is, by 2030Problem 2030), we have that \(f(\zeta )\neq Q\) for all \(\zeta \in \partial D(P,r)\), that is, that \(Q\in \C \setminus f(\partial D(P,r))\).Let \(U\) be the connected component of \(\C \setminus f(\partial D(P,r))\) containing \(Q\). Then \(U\) is open. Thus we need only prove that \(U\subseteq f(\Omega )\).
We have that there is (counted with multiplicity) at least one solution to \(f(z)=Q\) in \(D(P,r)\), namely \(z=P\). Thus, by 3090Problem 3090, \(\Ind _{f\circ \gamma }(Q)>0\).
By 2540Problem 2540, \(\Ind _{f\circ \gamma }\) is constant on connected components of
\begin{equation*}\C \setminus \widetilde {f\circ \gamma }=\C \setminus f(\widetilde \gamma )=\C \setminus f(\partial D(P,r)).\end{equation*}In particular, \(\Ind _{f\circ \gamma }(w)=\Ind _{f\circ \gamma }(Q)>0\) for all \(w\in U\). Using 3090Problem 3090 again, we see that if \(w\in U\) then \(w=f(\zeta )\) for at least one \(\zeta \in D(P,r)\subset \Omega \). Thus \(w\in f(\Omega )\) for all \(w\in U\) and so \(U\subseteq f(\Omega )\), as desired.
Give an example of an open set \(\Omega \subseteq \R ^2\) and a non-constant \(C^\infty \) function \(f:\Omega \to \R ^2\) such that \(f(\Omega )\) is not open.
Let \(f(x,y)=(x^2+y^2,2xy)\) and let \(\Omega =\R ^2\). Then \((0,0)=f(0,0)\in f(\R ^2)\) but \(f(\R ^2)\subseteq [0,\infty )\times \R \), so \((0,0)\in f(\R ^2)\) is a boundary point of \(f(\R ^2)\) and so \(f(\R ^2)\) cannot be open.
Let \(\Omega \subseteq \C \) be open, let \(P\in \Omega \), and let \(f:\Omega \setminus \{P\}\to \C \) be holomorphic. Suppose that \(f\) has an essential singularity at \(P\). If \(r>0\), show that \(f\) is not one-to-one on \(D(P,r)\cap \Omega \setminus \{P\}\).
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic and not constant. Let \(P\in \Omega \) and let \(Q=f(P)\).
Then there exists a \(\delta _0>0\) such that, if \(0<\delta <\delta _0\), then there exists a \(\varepsilon >0\) such that if \(w\in D(Q,\varepsilon )\setminus \{Q\}\) then there is at least one \(z\in D(P,\delta )\) such that \(f(z)=w\).
Let \(\Omega \subset \C \) be open, connected, and bounded, and let \(f:\overline \Omega \to \C \) be continuous on \(\overline \Omega \) and holomorphic in \(\Omega \). Show that \(\partial (f(\Omega ))\subseteq f(\partial \Omega )\).
What can you say if \(\Omega \) is unbounded?
If \(\Omega =\emptyset \) or \(f(\Omega )=\{Q\}\) then \(\partial (f(\Omega )) = f(\Omega )=f(\overline \Omega )=f(\partial \Omega )\) and so we are done.Otherwise, let \(z\in \partial (f(\Omega ))\). Because \(\partial (f(\Omega ))\subset \overline {f(\Omega )}\), we have that
\begin{equation*}z=\lim _{n\to \infty } f(\zeta _n)\end{equation*}for some \(\zeta _n\in \Omega \).
By the open mapping theorem \(f(\Omega )\) is open and so contains none of its boundary points, and so \(z\neq f(\xi )\) for any \(\xi \in \Omega \).
If \(\{\zeta _n\}_{n=1}^\infty \) has a bounded subsequence \(\{\zeta _{n_k}\}_{k=1}^\infty \), then it has a convergent sub-subsequence \(\{\zeta _{n_{k_\ell }}\}_{\ell =1}^\infty \). Let \(\zeta =\lim _{\ell \to \infty } \zeta _{n_{k_\ell }}\). Then each \(\zeta _{n_{k_\ell }}\) is in \(\Omega \) and so \(\zeta \in \overline \Omega \). By continuity of \(f\) on \(\overline \Omega \) we have that
\begin{equation*}f(\zeta )=\lim _{\ell \to \infty } f(\zeta _{n_{k_\ell }})=\lim _{n\to \infty } f(\zeta _n)=z\end{equation*}because the limit of a subsequence must be the limit of the parent sequence if it exists. But \(z\neq f(\xi )\) for all \(\xi \in \Omega \), so \(\zeta \notin \Omega \). But \(\zeta \in \overline \Omega \) because each \(\zeta _{n_{k_\ell }}\in \Omega \), and so \(z=f(\zeta )\) for some \(\zeta \in \partial \Omega \).
If \(\Omega \) is bounded then \(\{\zeta _n\}_{n=1}^\infty \) has a bounded subsequence, and so by the above argument \(z=f(\zeta )\) for some \(\zeta \in \partial \Omega \). This completes the argument for 3170Problem 3170.
If \(\Omega \) is not bounded, we are left with the possibility that \(\{\zeta _n\}_{n=1}^\infty \) has no bounded subsequences. An elementary real analysis argument shows that \(\lim _{n\to \infty } |\zeta _n|=\infty \). Thus in this case
\begin{equation*}\partial (f(\Omega ))\subseteq f(\partial \Omega )\cup \{\lim _{n\to \infty } f(\zeta _n): \lim _{n\to \infty }|\zeta _n|=\infty \}.\end{equation*}In particular, if \(\lim _{|z|\to \infty } f(z)\) exists, then
\begin{equation*}\partial (f(\Omega ))\subseteq f(\partial \Omega )\cup \Bigl \{\lim _{|z|\to \infty } f(z)\Bigr \}.\end{equation*}
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic and not constant. Then \(P\in \Omega \) is a multiple point of \(f\) if the function \(g(z)=f(z)-f(P)\) has a zero of multiplicity at least \(2\) at \(P\). If \(f(P)=Q\) and \(g\) has a zero of multiplicity \(k\), we say that \(f(P)=Q\) with order \(k\).
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic and not constant. Then \(P\in \Omega \) is a simple point of \(f\) if it is not a multiple point of \(f\), that is, if the function \(g(z)=f(z)-f(P)\) has a zero of multiplicity \(1\) at \(P\). If \(f(P)=Q\), we say that \(f(P)=Q\) with order \(1\).
Let \(\Omega \subseteq \C \) be open and connected and let \(f:\Omega \to \C \) be holomorphic and not constant. Let \(P\in \Omega \) and let \(Q=f(P)\) with order \(k\).
Then there exists a \(\delta _0>0\) such that, if \(0<\delta <\delta _0\), then there exists a \(\varepsilon >0\) such that if \(w\in D(Q,\varepsilon )\setminus \{Q\}\) then there are exactly \(k\) points \(z_1,\dots ,z_k\in D(P,\delta )\) such that \(f(z_j)=w\). Furthermore, each \(z_j\) is a simple point.
In this problem we begin the proof of Theorem 5.2.2. Show that if \(P\in \Omega \), then \(P\) is a multiple point of \(f\) if and only if \(f'(P)=0\). Use this fact to show that, if \(P\in \Omega \), then there is a \(\varrho >0\) such that there are no multiple points in \(D(P,\varrho )\setminus \{P\}\subset \Omega \).
By Theorem 3.3.1, we have that there is an \(r>0\) such that \(D(P,r)\subseteq \Omega \) and such that\begin{equation*}f(z)=\sum _{n=0}^\infty \frac {f^{(n)}(P)}{n!}(z-P)^n\end{equation*}for all \(z\in D(P,r)\). The function \(g(z)=f(z)-f(P)\) satisfies
\begin{equation*}g(z)=\sum _{n=1}^\infty \frac {f^{(n)}(P)}{n!}(z-P)^n\end{equation*}for all \(z\in D(P,r)\). By definition, the order of the zero of \(g\) at \(P\) is the smallest \(n\) such that the coefficient \(\frac {f^{(n)}(P)}{n!}\) is nonzero, that is, the smallest \(n\geq 1\) such that \(f^{(n)}(P)\neq 0\). Thus \(P\) is a simple point for \(f\) if and only if \(f'(P)\neq 0\).
By Corollary 3.1.2 \(f'\) is holomorphic. By assumption \(f\) is not constant and so \(f'\) is not identically zero in \(\Omega \). Thus by 2030Problem 2030 there is a \(\varrho >0\) such that \(D(P,\varrho )\subseteq \Omega \) ans such that \(f'\) has no zeroes, and thus \(f\) has no multiple points, in \(D(P,\varrho )\setminus \{P\}\).
Let \(R>0\) be such that \(z=P\) is the only solution in \(D(P,R)\) to \(f(z)=f(P)\). Such an \(R\) must exist by 2030Problem 2030. Let \(\varrho \) be as in 3190Problem 3190, and let \(0<\delta <\min (R,\varrho )\). Let \(U\) be the connected component of \(\C \setminus f(\partial D(P,\delta ))\) containing \(Q\); recall from 3120Memory 3120 that \(U\) is open. Suppose that \(w\in U\setminus \{Q\}\). Show that there are exactly \(k\) points \(z_1,\dots ,z_k\in D(P,\delta )\setminus \{P\}\) with \(f(z_j)=w\).
As in the proof of the Open Mapping Theorem, we have that \(\Ind _{f\circ \gamma } (w)=k\) for every \(w\in Q\), and so the number of solutions (with multiplicity) to \(f(z)=w\) in \(D(P,r)\) must be \(k\). But because every point in \(D(P,r)\setminus \{P\}\) is simple, this must mean \(k\) distinct solutions.
Prove Theorem 5.2.2.
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be holomorphic. Let \(P\in \Omega \) and suppose that \(f'(P)\neq 0\). Show that there is a \(r>0\) with \(D(P,r)\subseteq \Omega \) and such that \(f\) is one-to-one on \(D(P,r)\).
Let \(Q=f(P)\). By 3190Problem 3190, \(P\) is a simple point of \(f\). Thus, by Theorem 5.2.2, there is a \(\varepsilon >0\) and a \(\delta >0\) such that if \(w\in D(Q,\varepsilon )\) then there is exactly one solution \(z\in D(P,\delta )\) to the equation \(f(z)=w\). Let \(U=f^{-1}(D(Q,\varepsilon ))\cap D(P,\delta )\); observe that \(f\) is continuous and so \(\Omega \) is open. Thus, there is a \(r>0\) such that \(D(P,r)\subseteq U\).If \(\zeta \in D(P,r)\subseteq D(P,\delta )\), then there is precisely one solution \(z\) in \(D(P,\delta )\) to \(f(z)=f(\zeta )\); it is necessarily \(z=\zeta \). Thus, \(f\) must be one-to-one on \(D(P,r)\).
This may also be established using the Inverse Function Theorem of real analysis, but this proof is shorter and involves techniques that you have probably seen more recently.
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be holomorphic. Let \(P\in \Omega \) and suppose that \(f'(P)=0\). Show that there does not exist a \(r>0\) with \(D(P,r)\subseteq \Omega \) and such that \(f\) is one-to-one on \(D(P,r)\).
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \) be holomorphic and one-to-one. Let \(W=f(\Omega )\). Show that \(f^{-1}:W\to \Omega \) is continuous.
The statement is vacuous if \(\Omega =\emptyset \) so we assume \(\Omega \) is not empty; because it is open each connected component must contain infinitely many points. Because \(f\) is one-to-one, \(f\) cannot be constant on any connected component.By the Open Mapping Theorem, if \(U\subseteq \Omega \) is open, then \((f^{-1})^{-1}(U)=f(U)\) is open. Thus, the preimages of all open sets in \((f^{-1})(W)=\Omega \) under \(f^{-1}\) are open. Thus, \(f^{-1}\) is continuous.
Let \(\Omega \) be open and connected and let \(f:\Omega \to \C \) be holomorphic and injective. Then \(f^{-1}:f(\Omega )\to \Omega \) is also holomorphic.
[Rouché’s theorem.] Let \(\Omega \subseteq \C \) be open. Let \(f:\Omega \to \C \) and \(g:\Omega \to \C \) be holomorphic. Suppose that \(\overline D(P,r)\subseteq \Omega \) and that
for all \(z\in \partial D(P,r)\). Then \(f\) and \(g\) have the same number of zeroes (counted with multiplicities) in \(D(P,r)\).
In this problem we show an example of an application of Rouché’s theorem. The polynomial \(p(z)=z^{7}+4z^2+2\) has seven zeroes (with multiplicity). Use Rouché’s theorem to determine how many of these zeroes are in the disc \(D(0,1)\).
The polynomial \(p(z)=z^{7}+3z^2+2\) has seven zeroes (with multiplicity). Use Rouché’s theorem to determine how many of these zeroes are in the disc \(D(0,1)\).
Let \(g(z)=3z^2\) and let \(\Omega =\C \). Then \(g\) and \(p\) are holomorphic in \(\Omega \) and \(\overline D(0,1)\subset \Omega \). To use Rouché’s theorem we need only show that \(|g(z)-p(z)|<|g(z)|+|p(z)|\) for all \(z\in \partial D(0,1)\).We have that \(g(z)-p(z)=z^7+2\) and so \(|g(z)-p(z)|\leq |z^7|+2\) for all \(z\in \C \); if \(z\in \partial D(0,1)\) then \(|z|=1\) and so \(|g(z)-p(z)|\leq 3\).
Suppose that \(|g(z)-p(z)|=3\) and \(|z|=1\). Then \(|z^7+2|=3\). Thus
\begin{equation*}9=|z^7+2|^2=(z^7+2)(\overline z^7+2)=|z|^{14}+4\re (z^7)+4\end{equation*}and so \(\re z^7=1\). But \(|z^7|=1=\sqrt {(\re z^7)^2+(\im z^7)^2}\) and so \(\im z^7=0\). Thus \(z^7=1\) and so \(z=e^{2\pi ik/7}\) for some \(k\in \Z \).
If \(z=e^{2\pi ik/7}\) for some \(k\in \Z \), then \(p(z)=z^{7}+3z^2+2=3+3z^2=3(1+e^{4\pi ik/7})\). There is no \(k\in \Z \) such that \(e^{4\pi ik/7}=-1=e^{i\pi }\), and so if \(|g(z)-p(z)|=3\) then \(|p(z)|\neq 0\).
Thus, if \(|z|=1\) then either \(|g(z)-p(z)|<3=|g(z)|\leq |g(z)|+|p(z)|\), or \(|g(z)-p(z)|=3=|g(z)|<|g(z)|+|p(z)|\). In either case \(|g(z)-p(z)|<|g(z)|+|p(z)|\) and so we may apply Rouché’s theorem to see that \(g\) and \(p\) have the same number of zeroes (with multiplicity) in \(D(0,1)\). Since \(g\) has a single zero of multiplicity 2 at \(z=0\), we know that \(p\) has two zeroes (with multiplicity) in \(D(0,1)\).
In this problem we begin the proof of Rouché’s theorem. Let \(\eta \), \(\phi :[0,1]\to \C \) be two \(C^1\) closed curves. Suppose that
for all \(0\leq t\leq 1\). Show that \(\eta \) and \(\phi \) are homotopic in \(\C \setminus \{0\}\).
Let \(\Psi (t,s)=s\eta (t)+(1-s)\phi (t)\). Then \(\Psi \) is clearly \(C^1\) in both \(t\) and \(s\) and satisfies \(\Psi (t,0)=\phi (t)\), \(\Psi (t,1)=\eta (t)\), so \(\Psi \) is a \(C^1\) homotopy between \(\phi \) and \(\eta \).It remains to show that \(\Psi :[0,1]\times [0,1]\to \C \setminus \{0\}\), that is, that \(0\) is not in the image of \(\Psi \). Suppose for the sake of contradiction that \(\Psi (t,s)=0\). Then
\begin{equation*}0=s\eta (t)+(1-s)\phi (t).\end{equation*}If \(s=0\) then \(\phi (t)=0\) and so \(|\eta (t)-\phi (t)|=|\eta (t)|=|\eta (t)|+|\phi (t)|\), which is a contradiction.
If \(s\neq 0\) then \(\eta (t)=\frac {s-1}{s}\phi (t)\). Then
\begin{equation*} |\eta (t)-\phi (t)| =\biggl |\biggl (\frac {s-1}{s}-1\biggr )\phi (t)\biggr | =\biggl |\frac {1}{s}\biggr ||\phi (t)|.\end{equation*}But \(s>0\), so \(|\frac {1}{s}|=\frac {1}{s}\) and so
\begin{align*}|\eta (t)-\phi (t)|&=\frac {1}{s}|\phi (t)| =(1+\frac {1-s}{s})|\phi (t)| =|\phi (t)|+\frac {1-s}{s}|\phi (t)|.\end{align*}But \(s\leq 1\), so \(\frac {1-s}{s}\geq 0\) and so \(\frac {1-s}{s}=|\frac {1-s}{s}|\). Thus
\begin{equation*}|\eta (t)-\phi (t)|=|\phi (t)|+|\eta (t)| .\end{equation*}This is again a contradiction.
Prove Rouché’s theorem. Hint: Use 2550Problem 2550 and 3090Problem 3090.
Let \(\gamma (t)=P+re^{it}\), \(0\leq t\leq 2\pi \). Then \(\gamma \) is a \(C^1\) closed curve. If \(\eta =f\circ \gamma \) and \(\phi =g\circ \gamma \), then by the multivariable chain rule \(\eta \) and \(\phi \) are also \(C^1\) closed curves.But
\begin{align*}|\phi (t)-\eta (t)| &=|f(\gamma (t))-g(\gamma (t))| \neq |f(\gamma (t))|+|g(\gamma (t))|=|\phi (t)|+|\eta (t)| \end{align*}because \(\gamma (t)\in \partial D(P,r)\) for all \(t\), and so by the previous problem \(\eta \) and \(\phi \) are homotopic in \(\C \setminus \{0\}\).
Thus by 2550Problem 2550 \(\Ind _\eta (0)=\Ind _\phi (0)\).
But by 3090Problem 3090 \(\Ind _\eta (0)\) is the number of zeroes of \(f\) in \(D(P,r)\) with multiplicity and \(\Ind _\phi (0)\) is the number of zeroes of \(g\) in \(D(P,r)\), so they must be equal, as desired.
(The maximum modulus principle.) Let \(\Omega \subseteq \C \) be a connected open set and let \(f:\Omega \to \C \) be holomorphic. Suppose that there is a \(w\in \Omega \) such that \(|f(w)|\geq |f(z)|\) for all \(z\in \Omega \). Then \(f\) is constant.
Prove the maximum modulus principle. Hint: Show that \(f(\Omega )\) is not open.
We will prove the contrapositive. Suppose that \(f\) is not constant and \(w\in \Omega \); we need only show that \(|f(z)|>|f(w)|\) for some \(z\in \Omega \).By Theorem 5.2.1, \(f(\Omega )\) is open and thus there is a \(r>0\) such that \(D(f(w),r)\subseteq f(\Omega )\). In particular, \(\zeta =f(w)+r\frac {f(w)}{|f(w)|}\in f(\Omega )\) if \(f(w)\neq 0\) and \(\zeta =r/2\in f(\Omega )\) if \(f(w)=0\).
But then either \(|\zeta |=|f(w)+r\frac {f(w)}{|f(w)|}|=|f(w)|(1+r/2|f(w)|)>|f(w)|\) or \(|\zeta |=|r/2|=r/2>0=|f(w)|\), and so in either case \(|\zeta |>|f(w)|\).
But by definition of \(f(\Omega )\) we have that \(\zeta =f(z)\) for some \(z\in \Omega \), and so \(|f(z)|>|f(w)|\) for some \(z\in \Omega \), as desired.
(The maximum modulus principle, sharpened.) Let \(\Omega \subseteq \C \) be a connected open set and let \(f:\Omega \to \C \) be holomorphic. Suppose that there is a \(r>0\) and a \(w\in \Omega \) such that \(D(w,r)\subseteq \Omega \) and such that \(|f(w)|\geq |f(z)|\) for all \(z\in D(w,r)\). Then \(f\) is constant.
Prove Theorem 5.4.4.
(The maximum modulus theorem.) Let \(\Omega \subseteq \C \) be a bounded open set. Let \(f:\overline \Omega \to \C \) be continuous on \(\overline \Omega \) and holomorphic on \(\Omega \). Then there is a \(w\in \partial \Omega \) such that \(|f(w)|\geq |f(z)|\) for all \(z\in \overline \Omega \).
Prove Corollary 5.4.3.
\(\overline \Omega \) is a closed bounded subset of \(\C =\R ^2\), and so by the Heine-Borel theorem \(\overline \Omega \) is compact.Since \(f\) is continuous on \(\overline \Omega \), so is \(|f|\). Because real-valued continuous functions on compact sets attain their maxima, there is a \(\zeta \in \overline \Omega \) such that \(|f(\zeta )|\geq |f(z)|\) for all \(z\in \Omega \).
If \(\zeta \in \partial \Omega \) then we may choose \(w=\zeta \) and so are done. Otherwise, by the maximum modulus principle \(f\) is constant on the connected component \(U\) of \(\Omega \) containing \(\zeta \). Because \(\Omega \) is bounded, there is at least one point \(w\in \partial U\). It is an elementary argument in real analysis to show that \(\partial U\subseteq \partial \Omega \). Because \(f\) is continuous on \(\overline \Omega \supseteq \overline U\), we have that \(|f(w)|=|f(\zeta )|\geq |f(z)|\) for all \(z\in \overline \Omega \). This completes the proof.
Give an example of an unbounded connected open set \(\Omega \) with nonempty boundary and a continuous function \(f:\overline \Omega \to \C \) such that \(f\) is holomorphic in \(\Omega \) and such that \(|f(w)|<\sup _{z\in \overline \Omega } |f(z)|\) for all \(w\in \overline \Omega \). Bonus: Can you give an example in which \(f\) is bounded in \(\Omega \) and another example in which \(f\) is bounded on \(\partial \Omega \) but unbounded in \(\Omega \)?
Let \(\Omega =\{x+iy:x>0\}\) be the right half plane and let \(f(z)=\exp (z)\). Then \(|f(z)|=1\) for all \(z\in \partial \Omega \) but \(|f|\) is unbounded in \(\Omega \).Now let \(g(z)=\frac {z}{z+1}\). Then \(\lim _{z\to \infty } |g(z)|=1\) and so we may find \(z\) such that \(|g(z)|\) is arbitrarily close to \(1\), but if \(|g(z)|\geq 1\) then \(\re z\leq -1/2\) and so \(|g|\) cannot achieve its maximum in \(\overline \Omega \).
(The minimum modulus principle.) Let \(\Omega \subseteq \C \) be a connected open set and let \(f:\Omega \to \C \) be holomorphic. Suppose that there is a \(w\in \Omega \) such that \(|f(w)|\leq |f(z)|\) for all \(z\in \Omega \). Then either \(f\) is constant or…
Finish the statement of Proposition 5.4.5 and prove that your claim is correct.
Either \(f\) is constant or \(f(w)=0\).The proof is as follows. If \(f(w)=0\) then we are done, so suppose that \(f(w)\neq 0\). Then \(0<|f(w)|\leq |f(z)|\) for all \(z\in \Omega \), and so \(f\) is never zero.
Let \(g(z)=1/f(z)\); then \(g\) is also holomorphic in \(\Omega \). Furthermore, \(|g(z)|=1/|f(z)|\leq 1/|f(w)|=|g(w)|\) for all \(z\in \Omega \), and so by the maximum modulus principle (Theorem 5.4.2) \(g\) is constant. Thus \(f\) is constant, as desired.
Let \(h:D(0,R)\to \C \) be holomorphic for some \(R>0\). If \(|h(z)|=1\) for all \(z\in \partial \D \), then \(h\) is a rational function.
[Hurwitz’s theorem.] Let \(\Omega \subseteq \C \) be a connected open set. If \(k\in \N \), let \(f_k:\Omega \to \C \setminus \{0\}\) be a nowhere zero holomorphic function. Suppose that \(f_k\to f\), uniformly on compact subsets of \(\Omega \). Suppose that \(f(w)\neq 0\) for at least one \(w\in \Omega \). Then \(f(z)\neq 0\) for all \(z\in \Omega \).
Give an example of a connected open set \(\Omega \subseteq \C \) and a sequence of holomorphic functions \(f_k:\Omega \to \C \setminus \{0\}\) such that \(f_k(z)\neq 0\) for all \(z\in \Omega \) and all \(k\in \N \) but such that \(f_k\to 0\) uniformly on all compact subsets of \(\Omega \).
Let \(\Omega =\C \) and let \(f_k(z)=\frac {1}{k}e^z\). Then \(f_k\to 0\) uniformly on all compact sets, but \(f_k(z)\neq 0\) for all \(k\) and \(z\).
Prove Hurwitz’s theorem.
By Theorem 3.5.1, \(f\) is holomorphic. Suppose that \(f\) is not identically zero, and for the sake of contradiction suppose that \(f(P)=0\) for some \(P\in \Omega \).Then by 2030Problem 2030 (a corollary of Theorem 3.6.1), the zeroes of \(f\) are isolated. Thus, there is a \(R>0\) such that \(f\neq 0\) in \(D(P,R)\setminus \{P\}\).
Let \(0<r<R\). Then \(f\neq 0\) on \(\partial D(P,r)\). \(|f|\) is continuous, so \(|f|\) attains its minimum on the compact set \(\partial D(P,r)\). Let \(m=\min _{z\in \partial D(P,r)} |f(z)|>0\) and let \(\varepsilon =m/3\).
The set \(\overline D(P,r)\) is compact and so \(f_k\to f\) uniformly on \(\overline D(P,r)\). In particular, there is a \(k\in \N \) such that \(|f_k(z)-f(z)|<\varepsilon \) for all \(z\in \overline D(P,r)\).
By the triangle inequality, \(|f_k(z)|\geq |f(z)|-\varepsilon \geq 2m/3\) for all \(z\in \partial D(P,r)\). Because \(f_k\neq 0\), the minimum modulus principle applies in \(D(P,r)\) and so \(|f_k|\geq 2m/3\) in \(D(P,r)\). In particular \(|f_k(P)|\geq 2m/3\). Again by the triangle inequality \(|f(P)|\geq |f_k(P)|-|f_k(P)-f(P)| > m/3>0\) and so \(f(P)\neq 0\), contradicting our assumption. This completes the proof.
Let \(\Omega \subseteq \C \) be a connected open set. If \(k\in \N \), let \(f_k:\Omega \to \C \) be an injective holomorphic function. Suppose that \(f_k\to f\), uniformly on compact subsets of \(\Omega \). Show that \(f\) is either constant or injective.
We will let \(\D =D(0,1)\).
(Schwarz’s lemma.) Let \(f:\D \to \C \) be a function such that
Then we have that both of the following statements are true:
If in addition either
then there is a \(\theta \in \R \) such that \(f(z)=ze^{i\theta }\) for all \(z\in \D \).
Let \(f:\D \to \D \) be holomorphic with \(f(0)=0\). Begin the proof of Schwarz’s lemma by proving that \(|f'(0)|\leq 1\) and that \(|f(z)|\leq |z|\) for all \(z\in \D \).
Define\begin{equation*}g(z)=\begin {cases}f(z)/z, &z\in \D \setminus \{0\},\\f'(0),&z=0.\end {cases}\end{equation*}\(g\) is clearly holomorphic on \(\D \setminus \{0\}\). By definition of the complex derivative and because \(f(0)=0\),
\begin{equation*}f'(0)=\lim _{z\to 0} \frac {f(z)-f(0)}{z-0}=\lim _{z\to 0}\frac {f(z)}{z}\end{equation*}and in particular the limit exists. Thus by Theorem 2.3.3 and Corollary 3.1.2 we have that \(g\) is holomorphic at \(0\) and thus on \(\D \).
If \(0<\varepsilon <1\) and \(|z|=1-\varepsilon \), then \(|g(z)|= \frac {|f(z)|}{|z|}\leq \frac {1}{1-\varepsilon }\). \(g\) is holomorphic on \(D(0,1-\varepsilon )\) and continuous on \(\overline D(0,1-\varepsilon )\), and so we may apply the maximum modulus principle to see that \(|g(z)|\leq \frac {1}{1-\varepsilon }\) for all \(z\in D(0,1-\varepsilon )\). Taking the limit as \(\varepsilon \to 0^+\) we have that \(|g(z)|\leq 1\) for all \(z\in \D \). Recalling the definition of \(g\) completes the proof.
Complete the proof of Schwarz’s lemma. That is, suppose that in addition either \(|f(z)|=|z|\) for some \(z\in \D \) or \(|f'(0)|=1\). Show that there is a \(\theta \in \R \) such that \(f(z)=ze^{i\theta }\) for all \(z\in \D \).
Let \(g\) be as in the previous proof. By the previous problem, \(|g(z)|\leq 1\) for all \(z\in \D \). If \(|f'(0)|=1\) or \(|f(w)|=|w|\) for some \(w\in \D \setminus \{0\}\), then \(|g(w)|=1\) for some \(w\in \D \). By the maximum modulus principle \(g\) is constant in \(\D \), so there is an \(\alpha \in \C \) such that \(g(z)=\alpha \) or \(f(z)=\alpha z\) for all \(z\in \D \). Since \(\alpha =g(w)\), we have \(|\alpha |=|g(w)|=1\) and so \(\alpha =e^{i\theta }\) for some \(\theta \in \R \).
Let \(c\in \D \) and define
Then \(\phi _c\) is a holomorphic bijection from \(\D \) to itself, a continuous bijection from \(\partial \D \) to itself, and a continuous bijection from \(\overline \D \) to itself.
In this problem we begin the proof of 3390Lemma 3390. Show that \(\phi _c\) is holomorphic on \(\D \) and continuous on \(\overline \D \).
Show that \(\phi _c(\D )\subseteq \D \) and that \(\phi _c(\partial \D )\subseteq \partial \D \).
Let \(z\in \partial \D \); then \(z=e^{i\theta }\) for some \(\theta \in \R \). We compute\begin{equation*} \phi _c(e^{i\theta })=e^{i\theta }\frac {1-ce^{-i\theta }}{1-\overline ce^{i\theta }}.\end{equation*}Let \(w=1-ce^{-i\theta }\); because \(|c|<1\) we have that \(w\neq 0\) and so \(|w|=|\bar w|\neq 0\). Thus
\begin{equation*}|\phi _c(e^{i\theta })=\left |e^{i\theta }\frac {w}{\bar w}\right |=1.\end{equation*}Since \(z=e^{i\theta }\) was an arbitrary point of \(\partial \D \), we have that \(\phi _c(\partial \D )\subseteq \partial \D \).
We now observe that \(\phi _c\) is not a constant function. In particular, \(\phi _0(z)=z\), and if \(c\neq 0\) then \(\phi _c(c)=0\) and \(\phi _c(0)=-c\), so in either case \(\phi _c\) is not a constant.
Because \(\phi _c\) is holomorphic and not constant in \(\D \) and continuous on \(\overline \D \), by the maximum modulus principle and the maximum modulus theorem we have that if \(z\in \D \) then \(|\phi _c(z)|< \sup _{\partial \D } |\phi _c|=1\). So \(\phi _c(\D )\subseteq \D \).
Show that \(\phi _c(\phi _{-c}(z))=z\) for all \(z\in \overline \D \).
Because \(\phi _{-c}(\overline \D )\subseteq \overline \D \) and \(\phi _c\) is defined on \(\overline \D \), we have that \(\phi _{-c}\circ \phi _c\) is well defined on \(\overline \D \). For all such \(z\),\begin{align*} \phi _c(\phi _{-c}(z)) &=\frac {\phi _{-c}(z)-c}{1-\overline c \phi _{-c}(z)} \\&=\frac {(1+\overline c z)\phi _{-c}(z)-c(1+\overline c z)}{(1+\overline c z)-(1+\overline c z)\overline c \phi _{-c}(z)} \\&=\frac {z+c-c(1+\overline c z)}{(1+\overline c z)-(c+z)\overline c } \\&=\frac {z(1-c\overline c)}{1-c\overline c} =z. \end{align*}
Show that \(\phi _c(\D )=\D \) and that \(\phi _c(\partial \D )=\partial \D \). This completes the proof of 3390Lemma 3390.
We have shown that \(\phi _c(\D )\subseteq \D \). Conversely, let \(w\in \D \). Then \(\phi _{-c}(w)\in \D \) so \(w=\phi _c(\phi _{-c}(w))\in \phi _c(\D )\). Thus \(\D \subseteq \phi _c(\D )\) and so \(\D =\phi _c(\D )\).Similarly \(\phi _c(\partial \D )=\partial \D \).
We will now establish some further properties of \(\phi _c\). Show that
If \(\theta \in \R \), show that \(\phi _c(e^{i\theta }z) = e^{i\theta } \phi _{ce^{-i\theta }}(z)\).
If \(c\), \(w\in \D \), show that \(\phi _c\circ \phi _w=e^{i\theta }\phi _b\) for some \(b\in \D \) and some \(\theta \in \R \).
We compute\begin{align*} \phi _c(\phi _{w}(z)) &=\frac {\phi _{w}(z)-c}{1-\overline c \phi _{w}(z)} \\&=\frac {(1-\overline w z)\phi _{w}(z)-c(1-\overline w z)}{(1-\overline w z)-(1-\overline w z)\overline c \phi _{w}(z)} \\&=\frac {(z- w)-c(1-\overline w z)}{(1-\overline w z)-(z- w)\overline c } \\&=\frac {z(1+c\overline w)- (w+c)}{1+ w\overline c-(\overline w +\overline c)z } \\&= \frac {1+c\overline w}{1+ w\overline c} \frac {z- b}{1-\overline b z } \end{align*}where \(b=\frac {c+w}{1+c\overline w}=\phi _{-w}(c)\in \D \). Because \(\overline {1+c\overline w}=1+w\overline c\), we have that \(|\frac {1+c\overline w}{1+ w\overline c}|=1\) and so \(\frac {1+c\overline w}{1+ w\overline c}=e^{i\theta }\) for some \(\theta \in \R \).
Let \(G=\{f:f(z)=e^{i\theta }\phi _c(z)\) for some \(\theta \in \R \) and some \(c\in \D \}\). Show that \(G\) is a group (with function composition as the group action) and is a subgroup of the group of all holomorphic bijections from \(\D \) to itself.
Let \(f:\D \to \D \) be holomorphic. Let \(a\in \D \) and let \(b=f(a)\). Let \(g=\phi _b\circ f\circ \phi _{-a}\). Show that \(g\) satisfies the conditions of Schwarz’s lemma (Theorem 5.5.1).
By 3390Lemma 3390 we have that \(\phi _{-a}:\D \to \D \) and is holomorphic. By assumption \(f:\D \to \D \) and is holomorphic. Again by 3390Lemma 3390 we have that \(\phi _b:\D \to \D \) and is holomorphic. Thus \(g:\D \to \D \), and by Problem 1.49 in your book \(g\) is holomorphic.Finally, \(g(0)=\phi _b(f(\phi _{-a}(0)))=\phi _b(f(a))=\phi _b(b)=0\).
Apply Schwarz’s lemma to \(g\) to derive an upper bound on \(|f'(a)|\).
By Schwarz’s lemma \(|g'(0)|\leq 1\), and if \(|g'(0)|=1\), then \(g\) is a rotation.By the chain rule (Problem 1.49 in your book), \(g'(0)=\phi _b'(f(\phi _{-a}(0)))\cdot f'(\phi _{-a}(0))\cdot \phi _{-a}'(0)\). So
\begin{align*} 1&\geq |g'(0)| =|\phi _b'(b)||f'(a)||\phi _{-a}'(0)| \\&=\frac {1}{1-|b|^2} |f'(a)| \frac {1-|a|^2}{1} . \end{align*}This simplifies to
\begin{equation*}|f'(a)|\leq \frac {1-|f(a)|^2}{1-|a|^2}.\end{equation*}
Under what conditions (on \(f\)) is it the case that \(|g'(0)|=1\)? If these conditions hold, what must be true about \(f\)?
We observe that \(|g'(0)|=1\) if and only if \(|f'(a)|= \frac {1-|f(a)|^2}{1-|a|^2}\).Thus, if \(|f'(a)|=\frac {1-|b|^2}{1-|a|^2}\) then there is a \(\theta \in \R \) such that \(g(z)=e^{i\theta } z\).
We observe that \(f(z)=\phi _{-b}(g(\phi _a(z))) = \phi _{-b}(e^{i\theta }(\phi _a(z)))\). By 3450Problem 3450 and 3460Problem 3460, we have that \(f(z)=e^{i\alpha } \phi _c(z)\) for some \(c\in \D \) and some \(\alpha \in \R \), and so in particular \(f\) is a holomorphic bijection from \(\D \) to itself.
Let \(w\in \D \setminus \{a\}\). What does Schwarz’s lemma tell you about \(f(a)\) and \(f(w)\)?
Recall \(\phi _a(w)\in \D \). By Schwarz’s lemma, \(|g(\phi _a(w))|\leq |\phi _a(w)|\) and so\begin{align*} \left |\frac {f(w)-f(a)}{1-\overline {f(a)}\,f(w)}\right | &=\left |\frac {f(w)-b}{1-\overline {b}\, f(w)}\right | = |\phi _b(f(w))| =|\phi _b(f(\phi _{-a}(\phi _a(w))))| =|g(\phi _a(w))| \\&\leq |\phi _a(w)| =\left |\frac {w-a}{1-\overline a w}\right | .\end{align*}Furtermore, if we have equality then \(g\) must be a rotation, and so as in the previous problem there is an \(\alpha \in \R \) and a \(c\in \D \) such that \(f(z)=e^{i\alpha }\phi _c(z)\) for all \(z\in \D \).
[The Schwarz-Pick lemma.] Let \(f:\D \to \C \) be a function such that
Then we have that
If a nontrivial equality holds (either \(|f'(a)|=\frac {1-|f(a)|^2}{1-|z|^2}\) for some \(a\in \D \), or \(\left |\frac {f(a)-f(w)}{1-\overline {f(a)}f(w)}\right | = \left |\frac {a-w}{1-\overline {a}w}\right |\) for some \(a\), \(w\in \D \) with \(a\neq w\)), then there is a \(\theta \in \R \) and a \(c\in \D \) such that
for all \(z\in \D \).
Suppose that \(ad-bc\neq 0\). Show that if \(z\in \C \) and \(az+b=0\) then \(cz+d\neq 0\).
We say that a function \(f:\C \cup \{\infty \}\to \C \cup \{\infty \}\) is a fractional linear transformation if there exist numbers \(a\), \(b\), \(c\), \(d\in \C \) such that \(ad-bc\neq 0\) and such that
Let \(a\), \(b\), \(c\), and \(d\in \C \) with \(ad-bc\neq 0\). Let \(f\) be the fractional linear transformation given in Definition 6.3.1.
Then \(f\) is continuous as a function from \(\C \cup \{\infty \}\) to itself if we use the metric in 2930Problem 2930.
Furthermore, \(f\) is a bijection from \(\C \cup \{\infty \}\) to itself and its inverse is a fractional linear transformation.
Finally, if \(g\) is another fractional linear transformation then so is \(f\circ g\).
Begin the proof of Theorem 6.3.4 by showing that \(f\) is continuous as a function from \(\C \cup \{\infty \}\) to itself if we use the metric in 2930Problem 2930. Furthermore, show that \(f\) is the only continuous function from \(\C \cup \{\infty \}\) to itself that also satisfies \(f(z)=\frac {az+b}{cz+d}\) for all \(z\in \C \) such that \(cz+d\neq 0\).
Continue the proof of Theorem 6.3.4 by showing that \(f\) is one-to-one on \(\C \cup \{\infty \}\).
Suppose that \(f(z_1)=f(z_2)\) for some \(z_1\), \(z_2\in \C \cup \{\infty \}\).If \(f(z_1)=\infty \) then either \(z_1=\infty =z_2\) (if \(c=0\)) or \(z_1=-d/c=z_2\) (if \(c\neq 0\)). So in this case \(z_1=z_2\).
If \(f(z_1)=a/c=f(z_2)\) (implying \(c\neq 0\)), then either \(z_1=\infty \) or \(\frac {az_1+b}{cz_1+d}=a/c\), \(cz_1+d\neq 0\). But if \(\frac {az_1+b}{cz_1+d}=a/c\) then \(c(az_1+b)=a(cz_1+d)\), which may be simplified to \(ad-bc=0\), contradicting the definition of fractional linear transformation. Therefore \(z_1=\infty \). Similarly \(z_2=\infty \). Thus in this case \(z_1=z_2\).
Finally, suppose that \(f(z_1)=f(z_2)\neq \infty \) and \(f(z_1)=f(z_2)\neq a/c\). We must then have that \(cz_1+d\neq 0\neq cz_2+d\) and so \(\frac {az_1+b}{cz_1+d}=f(z_1)=f(z_2)=\frac {az_2+b}{cz_2+d}\). Cross-multiplying yields that \((az_1+b)(cz_2+d)=(az_2+b)(cz_1+d)\), which may be simplified to \((ad-bc)z_1=(ad-bc)z_2\). Because \(ad-bc\neq 0\), we may cancel the terms \(ad-bc\) to see that \(z_1=z_2\).
Thus, in any case, if \(f(z_1)=f(z_2)\) then \(z_1=z_2\).
Continue the proof of Theorem 6.3.4 by showing that the composition of two fractional linear transformations is a fractional linear transformation.
More precisely, let \(f\) and \(g\) be two fractional linear transformations and let \(a\), \(b\), \(c\), \(d\), \(\alpha \), \(\beta \), \(\gamma \), \(\delta \) be the complex numbers such that
Let \(\zeta \), \(\eta \), \(\theta \), \(\kappa \) be the complex numbers that satisfy
Show that \(\zeta \kappa -\eta \theta \neq 0\) and that, if \(h\) is the fractional linear transformation such that
then \(h=f\circ g\).
First observe that\begin{equation*}\zeta \kappa -\eta \theta =\det \begin {pmatrix}\zeta &\eta \\\theta &\kappa \end {pmatrix}\end{equation*}which we know from linear algebra to be equal to
\begin{equation*}\det \begin {pmatrix}a&b\\c&d\end {pmatrix} \cdot \det \begin {pmatrix}\alpha &\beta \\\gamma &\delta \end {pmatrix} .\end{equation*}Because \(f\) and \(g\) are fractional linear transformations, we know that
\begin{equation*}\det \begin {pmatrix}a&b\\c&d\end {pmatrix} \neq 0\neq \det \begin {pmatrix}\alpha &\beta \\\gamma &\delta \end {pmatrix} \end{equation*}and so \(\zeta \kappa -\eta \theta \neq 0\). Thus \(h\) is a fractional linear transformation; we need only show that \(h=f\circ g\).
To prove this, let \(\Omega =\{z\in \C :g(z)\in \C \) and \(f(g(z))\in \C \}\). The set \(\{z\in \C :g(z)\notin \C \}\) contains at most one point. Because \(f\) is one-to-one and maps \(\C \cup \{\infty \}\) to \(\C \cup \{\infty \}\), we have that \(\{z\in \C :g(z)\in \C ,\>f(g(z))\notin \C \}=\{z\in \C :g(z)\in \C ,\>g(z)=f^{-1}(\infty )\}\). But because \(g\) is one-to-one there is at most one \(z\in \C \) with \(g(z)=f^{-1}(\infty )\), and so \(\C \setminus \Omega \) contains at most two points.
If \(z\in \Omega \), then \(g(z)=\frac {\alpha z+\beta }{\gamma z+\delta }\) (because \(z\in \C \) and \(g(z)\neq \infty \)) and also \(f(g(z))=\frac {ag(z)+b}{cg(z)+d}\) (because \(g(z)\in \C \) and \(f(g(z))\neq \infty \)). It is then straightforward to compute that \(f(g(z))=h(z)\) for such \(z\).
We are left with the at most three points \(\infty \), \(g^{-1}(\infty )\), and \(g^{-1}(f^{-1}(\infty ))\). But \(h\) and \(f\circ g\) are continuous in the metric space of 2930Problem 2930, and so if they are equal on a dense set then they must be equal everywhere.
Let \(f\) be a fractional linear transformation. By 3540Problem 3540 \(f\) is one-to-one on \(\C \cup \{\infty \}\). Show that \(f\) is also surjective \(\C \cup \{\infty \}\mapsto \C \cup \{\infty \}\) and that \(f^{-1}\) is also a fractional linear transformation.
Let \(g(z)=\frac {dz-b}{-cz+a}\) if \(z\in \C \), \(-cz+a\neq 0\). Then \(da-(-b)(-c)=ad-bc\neq 0\) and so \(g\) is a fractional linear transformation. By 3550Problem 3550, the composition \(h=f\circ g\) satisfies \(h(z)=\frac {\zeta z+\eta }{\theta z+\kappa }\) whenever \(z\in \C \), and \(\theta z+\kappa \neq 0\), where\begin{equation*} \begin {pmatrix}\zeta &\eta \\\theta &\kappa \end {pmatrix} =\begin {pmatrix}a&b\\c&d\end {pmatrix} \begin {pmatrix}d&-b\\-c&a\end {pmatrix} =\begin {pmatrix}ad-bc&0\\0&ad-bc\end {pmatrix} .\end{equation*}Thus \(h(z)=z\) for all \(z\in \C \) (and \(h(\infty )=\infty \)), and so \(f\circ g(z)=z\) for all \(z\in \C \cup \{\infty \}\). Similarly \(g\circ f(z)=z\) for all \(z\in \C \cup \{\infty \}\). Thus \(f\) must be surjective and its inverse \(f^{-1}=g\) is another fractional linear transformation.
Let \(S\subset \C \cup \{\infty \}\).
If there is a \(w\in \C \) and a positive real number \(r>0\) such that \(S=\{z:|z-w|^2=r^2\}\), then we say that \(S\) is a circle. (Observe that circles by definition have positive radius.)
If there are real numbers \(\ell \), \(m\), and \(s\), with \(\ell \) and \(m\) not both zero, such that \(S=\{\infty \}\cup \{x+iy:x\in \R ,\>y\in \R ,\>\ell x+my=s\}\), then we say that \(S\) is a line. (Observe that lines include the point at \(\infty \) and circles do not.)
Let \(f\) be a fractional linear transformation and let \(S\subset \C \cup \{\infty \}\). If \(S\) is a circle, then \(f(S)\) is either a line or a circle, and if \(S\) is a line, then \(f(S)\) is either a line or a circle.
In this problem we begin the proof of Theorem 6.3.7. Specifically, we begin by examining the preimages of the particular circle \(\partial \D \) under fractional linear transformations. Let \(f\) be a fractional linear transformation. Let \(S=\{z\in \C \cup \{\infty \}:|f(z)|=1\}\). Show that \(S\cap \C \) and \(\C \setminus S\) both contain infinitely many points.
Let \(f\) be a fractional linear transformation and let \(a\), \(b\), \(c\), \(d\) be such that \(f(z)=\frac {az+b}{cz+d}\) whenever \(cz+d\neq 0\). Let \(S=\{z\in \C \cup \{\infty \}:|f(z)|=1\}\). Show that there exist real numbers \(\alpha \), \(\beta \), and \(\gamma \) such that
Suppose that \(z=x+iy\in S\cap \C \). If \(|f(z)|=1\), then \(f(z)\neq \infty \) and so \(cz+d\neq 0\).But if \(cz+d\neq 0\) and \(z\neq \infty \), then
\begin{equation*}f(z)=\frac {az+b}{cz+d}\end{equation*}and so if \(|f(z)|=1\) then \(|az+b|=|cz+d|\). Conversely, if \(|az+b|=|cz+d|\) then by 3520Problem 3520 we cannot have \(cz+d=0\) and so \(|f(z)|=1\).
Thus \(|f(z)|=1\) if and only if \(|az+b|=|cz+d|\). Because both sides are nonnegative real numbers, we have that \(|f(z)|=1\) if and only if \(|az+b|^2=|cz+d|^2\). Recalling that \(|w|^2=w\bar w\), we compute that \(|f(z)|=1\) if and only if
\begin{equation*}(az+b)(\bar a\bar z+\bar b)=(cz+d)(\bar c\bar z+\bar d).\end{equation*}We may easily see that this equation is equivalent to
\begin{equation*}(|a|^2-|c|^2)|z|^2+(a\bar b-c\bar d) z+(\bar a b-\bar c d) \bar z = (|d|^2-|b|^2) .\end{equation*}Let \(\gamma =|d|^2-|b|^2\); then \(\gamma \) is real.
The complex number \(2\bar ab-2\bar cd\) has real and imaginary parts; we may write \(2\bar ab-2\bar cd=\alpha +i\beta \) for \(\alpha \), \(\beta \in \R \). Then \(a\bar b-c\bar d\) is the conjugate of \(\bar a b-\bar c d\) and so \(a\bar b-c\bar d=\frac {1}{2}(\alpha -i\beta )\). Recall that if \(z=x+iy\), \(x\), \(y\in \R \), then \(|z|^2=x^2+y^2\). Then \(|f(z)|=1\) if and only if
\begin{align*} (|a|^2-|c|^2)(x^2+y^2)&+ \frac {1}{2}(\alpha -i\beta )(x+iy)+\frac {1}{2}(\alpha +i\beta )(x-iy) = \gamma .\end{align*}Multiplying out we have that \(|f(z)|=1\) if and only if
\begin{equation*}(|a|^2-|c|^2)(x^2+y^2)+ \alpha x+\beta y = \gamma \end{equation*}as desired.
If \(|a|\neq |c|\), show that \(S\) is a circle (of positive radius).
First observe that \(f(\infty )=a/c\) (if \(c\neq 0\)) or \(f(\infty )=\infty \) (if \(c=0\)), and so in either case, if \(|a|\neq |c|\), then \(|f(\infty )|\neq 1\). Thus \(S=S\cap \C \).By the previous problem we have that
\begin{equation*} S=\{x+iy:x\in \R ,\>y\in \R , \>(|a|^2-|c|^2)(x^2+y^2) +\alpha x+\beta y=\gamma \}.\end{equation*}Because \(|a|\neq |c|\) we may divide the equation by \(|a|^2-|c|^2\) to see that
\begin{equation*} S=\{x+iy:x\in \R ,\>y\in \R , \>x^2+y^2 +2\widetilde \alpha x+2\widetilde \beta y=\widetilde \gamma \}\end{equation*}for suitable real numbers \(\widetilde \alpha \), \(\widetilde \beta \) and \(\widetilde \gamma \). Completing the square, we see that
\begin{equation*} S=\{x+iy:x\in \R ,\>y\in \R , \>(x+\widetilde \alpha )^2+(y+\widetilde \beta )^2 =\delta \} \end{equation*}where \(\delta = \widetilde \gamma + \widetilde \alpha ^2 + \widetilde \beta ^2\). If \(\delta <0\) then \(S=\emptyset \). This contradicts 3560Problem 3560. If \(\delta =0\) then \(S=\{-\widetilde \alpha -i\widetilde \beta \}\) contains a single point, again contradicting 3560Problem 3560. Thus we must have \(\delta >0\) and so \(S\) is a circle, as desired.
If \(|a|=|c|\), show that \(S\) is a line (recall this means that \(\infty \in S\)).
Because \(ad-bc\neq 0\), we cannot have \(a=0=c\) and so we cannot have \(|a|=0=|c|\). Thus we must have \(|a|=|c|>0\) and so in particular \(c\neq 0\). Thus \(f(\infty )=a/c\), and so \(|f(\infty )|=|a|/|c|=1\), and so \(\infty \in S\).By 3570Problem 3570, if \(|a|=|c|\) then there are real numbers \(\alpha \), \(\beta \) and \(\gamma \) such that
\begin{equation*} S\cap \C =\{x+iy:x\in \R ,\>y\in \R , \>\alpha x+\beta y=\gamma \}.\end{equation*}If \(\alpha =\beta =0\), then \(\alpha x+\beta y =0\) for all \(x+iy\in \C \), and so either \(S\cap \C =\C \) (if \(\gamma =0\)) or \(S\cap \C =\emptyset \) (if \(\gamma \neq 0\)). In either case we have a contradiction to 3560Problem 3560. Thus we must have that at least one of \(\alpha \) and \(\beta \) is nonzero, and so we must have that \(S\) is a line, as desired.
Let \(S\subset \C \cup \{\infty \}\) be a circle of positive radius. Show that there is a fractional linear transformation \(f\) such that \(S=\{z\in \C \cup \{\infty \}:|f(z)|=1\}=f^{-1}(\partial \D )\).
If \(S\) is a circle, then \(S=\{z\in \C :|z-w|=r\}\) for some \(w\in \C \) and some \(r>0\). Let \(f(z)=\frac {z-w}{r}=\frac {1z-w}{0z+r}\); then \(r\neq 0 \) so \(1r-0(-w)\neq 0\) and \(f\) is a fractional linear transformation. Then \(1=|f(z)|=\left |\frac {z-w}{r}\right |=\frac {|z-w|}{r}\) if and only if \(|z-w|=r\) and so \(z\in S\), so \(S= \{z\in \C :|f(z)|=1\}\).
Let \(S\) be a line in \(\C \cup \{\infty \}\). Show that there is a fractional linear transformation \(f\) such that \(S=f^{-1}(\R \cup \{\infty \})\).
Recall that \(S\subset \C \cup \{\infty \}\) is a line if there are real numbers \(\ell \), \(m\) and \(s\), with \(\ell \) and \(m\) not both zero, such that\begin{equation*}S=\{\infty \}\cup \{x+iy:x\in \R ,\>y\in \R ,\>\ell x+my=s\}.\end{equation*}Observe that \(\ell x+my -s = \im ((m+i\ell )(x+iy)-is)\), and so we may write \(S=\{\infty \}\cup \{z\in \C :\im (\alpha z+\beta )=0\}\) for some \(\alpha \), \(\beta \in \C \) with \(\alpha \neq 0\).
Let \(f(z)=\alpha z+\beta \). Clearly \(f\) is a fractional linear transformation. If \(z\in \C \) then \(z\in S\) if and only if \(\im f(z)=0\), that is, if and only if \(f(z)\in \R \). Observe that \(f(\infty )=\infty \) and so \(\infty \in f^{-1}(\R \cup \{\infty \})\). Thus \(S=f^{-1}(\R \cup \{\infty \})\), as desired.
Let \(g(z)=\frac {z-i}{z+i}\) and let \(\H =\{z\in \C :\im z>0\}\). Then
Prove Theorem 6.3.6 and also show that \(\R \cup \{\infty \}=g^{-1}(\partial \D )\).
First, \(g(\infty )=1\in \partial \D \) and \(g(-i)=\infty \notin \partial \D \).If \(z\in \C \), \(z\neq -i\), then
\begin{align*} |g(z)|^2 &=\biggl (\frac {z-i}{z+i}\biggr ) \biggl (\frac {\bar z+i}{\bar z-i}\biggr ) = \frac {|z|^2 +1+iz-i\bar z}{|z|^2+1-iz+i\bar z} = \frac {|z|^2 +1-2\im z}{|z|^2+1+2\im z} .\end{align*}The numerator and denominator are equal if and only if \(\im z=0\); thus \(\R =g^{-1}(\partial \D )\setminus \{\infty \}\). We have seen \(\infty \in g^{-1}(\partial \D )\), and so \(\R \cup \{\infty \}=g^{-1}(\partial \D )\), as desired.
Because \(g\) is a bijection we have that \(g(\R \cup \{\infty \})=\partial \D \).
Because \(g\) is continuous, \(g(\H )\) is connected. Because \(g\) is one-to-one and \(g(\R \cup \{\infty \})=\partial \D \), we have \(g(\H )\cap \partial \D =\emptyset \). Thus \(g(\H )\) is contained in a connected component of \(\C \setminus \partial \D \), that is, either \(g(\H )\subseteq \D \) or \(g(\H )\subseteq \C \cup \{\infty \}\setminus \overline \D \). But \(i\in \H \) and \(g(i)=0\in \D \), so \(g(\H )\subseteq \D \).
By 3180Problem 3180 we have that \(\partial g(\H )\subseteq g(\partial \H )\cup \{\lim _{z\to \infty } g(z)\}\). But \(\partial \H =\R \) and \(\lim _{z\to \infty } g(z)=1\), and so \(\partial g(\H )\subseteq \partial \D \).
\(\D \) is connected, so if \(g(\H )\subsetneq \D \) then \(\partial g(\H )\) contains points of \(\D \). This is not true, so we must have \(g(\H )=\D \), as desired.
Let \(S\subset \C \cup \{\infty \}\) be a straight line. Show that there is a fractional linear transformation \(f\) such that \(S=\{z\in \C \cup \{\infty \}:|f(z)|=1\}=f^{-1}(\partial \D )\).
Let \(S\) be our arbitrary line. By the previous problems we can find fractional linear transformations \(h\) and \(g\) such that \(S=h^{-1}(\R \cup \{\infty \})\) and \(\R \cup \{\infty \}=g^{-1}(\partial \D )\). Then \(f=g\circ h\) is a fractional linear transformation and \(S=h^{-1}(\R \cup \{\infty \})=h^{-1}(g^{-1}(\partial \D )) =(g\circ h)^{-1}(\partial \D )\), as desired.
Complete the proof of Theorem 6.3.7 by showing that if \(f\) is any fractional linear transformation and \(S\) is either a line or a circle, then \(f(S)\) is also either a line or a circle.
By the above problems there is a fractional linear transformation \(h\) such that \(S=h^{-1}(\partial \D )\). Thus \(f(S)=(f\circ h^{-1})(\partial \D )\). But \(f\circ h^{-1}\) is a fractional linear transformation. Let \(\varphi =(f\circ h^{-1})^{-1}\), which is also a fractional linear transformation. Then \(f(S)=\varphi ^{-1}(\partial \D )\), which we have seen is either a line or a circle.
Let \(f(z)=\frac {z+1}{iz-i}\). Show that \(f(\D )=\H \), where \(\H =\{x+iy:x\in \R , y\in (0,\infty )\}\).
Let \(f(z)=\frac {z-1}{iz+i}\). Show that \(f(\{z\in \C :|z|<1,\>\im z>0\})=\{x+iy:x,y\in (0,\infty )\}\).
Find a fractional linear transformation \(f\) such that \(f(\{x+iy:x,y\in \R , x>y\})=D(3,4)\).
If \(f\) is a fractional linear transformation, \(c\) and \(C\) are concentric circles, and \(f(c)\) and \(f(C)\) are also concentric circles, then the ratio of the radii of \(c\) and \(C\) is equal to the ratio of the radii of \(f(c)\) and \(f(C)\).
State the Bolzano-Weierstraß theorem in \(\R ^p\). What does this tell you about bounded sequences in \(\C \)?
Show that every sequence in a compact set has a convergent subsequence.
Give an example of a sequence of bounded continuous real-valued functions on \([0,1]\subset \R \) that do not have a convergent subsequence.
Let \(\{f_n\}_{n=1}^\infty \) be a sequence of functions from \((X,d)\) to \((Y,\varrho )\), where \((X,d)\) and \((Y,\varrho )\) are two metric spaces. Suppose that for each \(x\in X\) and each \(\varepsilon >0\) there is a \(\delta =\delta _{\varepsilon ,x}>0\) such that if \(y\in X\) with \(d(x,y)<\delta _{\varepsilon ,x}\) then \(\sup _{n\in \N } \varrho (f_n(x),f_n(y))<\varepsilon \) (that is, \(\varrho (f_n(x),f_n(y))<\varepsilon \) for all \(n\in \N \), and \(\delta _{\varepsilon ,x}\) cannot depend on \(n\).) Then we say that the sequence \(\{f_n\}_{n=1}^\infty \) is equicontinuous.
If \(\delta =\delta _\varepsilon \) may be taken to be independent of \(x\), then the sequence is uniformly equicontinuous.
Suppose that \(\{f_n\}_{n=1}^\infty \) is an equicontinuous sequence of functions and that their common domain \((X,d)\) is compact. Show that \(\{f_n\}_{n=1}^\infty \) is uniformly equicontinuous.
The Arzelà-Ascoli Theorem. Let \((\Psi ,d)\) and \((Y,\rho )\) be compact metric spaces.4 Let \(\{f_n\}_{n=1}^\infty \) be an equicontinuous sequence of functions from \(\Psi \) to \(Y\). Then there is a subsequence \(\{f_{n_k}\}_{k=1}^\infty \) of \(\{f_n\}_{n=1}^\infty \) that converges uniformly on \(\Psi \).
In this problem we begin the proof of the Arzelà-Ascoli theorem. This problem is a strengthening of the known fact that compact sets are separable. Suppose that \(\Psi \) is compact and that for each positive number \(\varepsilon >0\) and each \(z\in \Psi \) we are given a positive number \(\delta _{\varepsilon ,z}>0\). Further suppose that if \(z\in \Psi \) and \(\varepsilon \leq \eta \) then \(\delta _{\varepsilon ,z}\leq \delta _{\eta ,z}\). Show that there exists a sequence \(\{z_m\}_{m=1}^\infty \subset \Psi \) such that, for each \(\varepsilon >0\), there is a \(M\in \N \) such that \(\Psi \subseteq \bigcup _{m=1}^M B(z_m,\delta _{\varepsilon ,z_m})\).
For each \(k\in \N \), the set \(\{B(z,\delta _{2^{-k},z}):z\in \Psi \}\) is an open cover of \(\Psi \). Thus it has a finite subcover. Let \(\{z_{k,j}:1\leq j\leq N_k\}\) be a set of finitely many points such that \(\Psi =\bigcup _{j=1}^{N_k} B(z_{k,j},\delta _{2^{-k},z})\).We may then define \(z_m\) such that \(z_m=z_{1,m}\) if \(1\leq m\leq N_1\), \(z_m=z_{2,m-N_1}\) if \(N_1<m\leq N_2\), and in general \(z_m=z_{k,m-N_1-\dots -N_{k-1}}\) for \(k\) the unique number such that \(N_1+\dots +N_{k-1}<m\leq N_1+\dots +N_k\).
If \(\varepsilon >0\), there is then a \(k\) such that \(2^{-k}<\varepsilon \); choosing \(M=N_1+\dots +N_k\) completes the proof.
Let \(\Psi \), \(Y\), and \(f_n\) be as in the Arzelà-Ascoli theorem. Let \(\{z_m\}_{m=1}^\infty \subseteq \Psi \) be a sequence. Show that there is one subsequence \(\{f_{n_k}\}_{k=1}^\infty \) of \(\{f_n\}_{n=1}^\infty \) (with \(n_k\) independent of \(m\)) such that \(\{f_{n_k}(z_m)\}_{k=1}^\infty \) is a convergent sequence for each \(m\in \N \).
Because \(\{f_n(z_1):n\in \N \}\) is bounded and (closed bounded subsets of) \(Y\) are compact, we have that some subsequence \(\{f_{n_{1,k}}(z_1)\}_{k=1}^\infty \) is convergent.Now, suppose that the strictly increasing sequence of natural numbers \(\{n_{j,k}\}_{k=1}^\infty \) has been defined and that \(\{f_{n_{j,k}}(z_m)\}_{k=1}^\infty \) converges for all \(m\leq j\). Then the sequence \(\{f_{n_{j,k}}(z_{j+1})\}_{k=1}^\infty \) is bounded, and so some subsequence converges. Define \(\{n_{j+1,k}\}_{k=1}^\infty \) to be a subsequence such that \(\{f_{n_{j+1,k}}(z_{j+1})\}_{k=1}^\infty \) converges; because \(\{n_{j+1,k}\}_{k=1}^\infty \) is a subsequence of \(\{n_{j,k}\}_{k=1}^\infty \), we have that \(\{f_{n_{j,k}}(z_m)\}_{k=1}^\infty \) converges for all \(m\leq j\) and thus all \(m\leq j+1\).
Define \(n_\ell \) by \(n_{\ell }=n_{\ell ,\ell }\). Because \(\{n_{j+1,k}\}_{k=1}^\infty \) is a subsequence of \(\{n_{j,k}\}_{k=1}^\infty \), we must have that \(n_{j+1,k+1}>n_{j+1,k}\) for all \(k\in \N \); in particular, \(n_{\ell +1,\ell +1}>n_{\ell +1,\ell }\). A straightforward induction argument shows that, because \(\{n_{\ell +1,k}\}_{k=1}^\infty \) is a subsequence of \(\{n_{\ell ,k}\}_{k=1}^\infty \), we must have \(n_{\ell +1,k}\geq n_{\ell ,k}\) for all \(k\in \N \); in particular \(n_{\ell +1,\ell }\geq n_{\ell ,\ell }\). Thus
\[n_{\ell +1}=n_{\ell +1,\ell +1}>n_{\ell +1,\ell }\geq n_{\ell ,\ell }\]and so \(\{n_\ell \}_{\ell =1}^\infty \) is a strictly increasing sequence of natural numbers; thus \(\{f_{n_\ell }\}_{\ell =1}^\infty \) is a subsequence of \(\{f_n\}_{n=1}^\infty \).
If \(m\in \N \), then \(\{n_\ell \}_{\ell =m}^\infty \) is a subsequence of \(\{n_{m,k}\}_{k=1}^\infty \), and therefore we must have that \(\{f_{n_{\ell }}(z_m)\}_{\ell =1}^\infty \) converges.
Let \((X,d)\) and \((Y,\varrho )\) be two metric spaces and suppose that \((Y,\varrho )\) is complete. Let \(f_n:X\to Y\) and suppose that \(\{f_n\}_{n=1}^\infty \) is uniformly Cauchy: for every \(\varepsilon >0\) there is a \(N\in \N \) such that if \(\ell \), \(k>N\) then \(\varrho (f_\ell (x),f_k(x))<\varepsilon \) for all \(x\in X\). Then \(\{f_n\}_{n=1}^\infty \) converges uniformly on \(X\).
Suppose in addition that \(z_m\) is as in 3690Problem 3690. Let \(\delta _{\varepsilon ,z}\) be as in the definition of equicontinuous sequence; we may assume without loss of generality that \(\delta _{\varepsilon ,z}\) is nondecreasing in \(\varepsilon \). Show that \(\{f_{n_k}\}_{k=1}^\infty \) is uniformly convergent on \(\Psi \).
Pick \(\varepsilon >0\).Let \(M\in \N \) be such that \(\Psi = \bigcup _{m=1}^M B(z_m,\delta _{\varepsilon ,z_m})\); by 3690Problem 3690, such an \(M\) exists.
Now, for each \(m\), the sequence \(\{f_{n_k}(z_m)\}_{k=1}^\infty \) converges in \(Y\), and therefore is a Cauchy sequence. By the definition of convergence, there is a \(N_m\) such that if \(k\), \(\ell \geq N_m\) then \(\rho (f_{n_k}(z_m),f_{n_\ell }(z_m))<\varepsilon \). Because \(M\) is finite, so is \(N=\max \{N_1,\dots ,N_M\}\).
Pick some \(k\), \(\ell \geq N\) and some \(z\in \Psi \). Then \(z\in B(z_\mu ,\delta _{\varepsilon ,z_\mu })\) for some \(\mu \leq M\) by definition of \(M\). We may then compute that
\begin{align*} \rho (f_{n_k}(z),f_{n_\ell }(z)) &\leq \rho (f_{n_k}(z),f_{n_k}(z_\mu )) \\&+\rho (f_{n_k}(z_\mu ),f_{n_\ell }(z_\mu )) \\&+\rho (f_{n_\ell }(z_\mu ),f_{n_\ell }(z)) \\&<3\varepsilon . \end{align*}Thus, for any \(\varepsilon >0\) there is a \(N\in \N \) (depending on \(\varepsilon \) alone) such that if \(k\), \(\ell \geq N\) then \(\rho (f_{n_k}(z),f(z))<3\varepsilon \) for all \(z\in \Psi \); thus \(\{f_{n_k}\}_{k=1}^\infty \) is uniformly Cauchy on \(\Psi \), and therefore by completeness of \(Y\) is uniformly convergent.
If \(\{f_n\}_{n=1}^\infty \) is a sequence of functions from an open set \(\Omega \subseteq \C \) to \(\C \), we say that \(\{f_n\}_{n=1}^\infty \) converges normally to \(f\) if \(\{f_n\}_{n=1}^\infty \) converges to \(f\) uniformly on compact subsets \(K\) of \(\Omega \).
If \(\mathcal {F}\) is a family of functions such that \(f:\Omega \to \C \) for each \(f\in \mathcal {F}\), and if every sequence in \(\mathcal {F}\) has a subsequence that converges normally, we say that \(\mathcal {F}\) is a normal family.
If each \(f_n\) is holomorphic and \(f_n\to f\) normally then \(f\) is holomorphic.
If each \(f_n\) is holomorphic and \(f_n\to f\) normally then \(f_n'\to f'\) normally.
[Montel’s theorem, first version.] Suppose that \(\mathcal {F}\) is a family of functions that are holomorphic on some open set \(\Omega \). Suppose that there is a constant \(M>0\) such that, if \(f\in {\mathcal {F}}\) and \(z\in \Omega \), then \(\abs {f(z)}\leq M\). Then \(\mathcal {F}\) is a normal family.
In this problem we begin the proof of Montel’s theorem. Let \(\{f_n\}_{n=1}^\infty \) be a sequence of holomorphic functions defined on an open set \(\Omega \subset \C \). Suppose that there is a \(M\in \R \) such that \(|f_n(z)|\leq M\) for all \(z\in \Omega \) and \(n\in \N \). Let \(\Psi \subset \Omega \) be compact. Show that the functions \(f_n\) satisfy the conditions of the Arzelà-Ascoli theorem (3681) on \(\Psi \).
\(\Psi \) is compact (under the standard topology on \(\C \)) by assumption, while \(Y=\overline D(0,M)\) is compact by the Heine-Borel theorem. Then \(f_n:\Psi \to Y\).We are left with equicontinuity. Because \(\Psi \subset \Omega \), \(\Psi \) is compact, and \(\Omega \) is open, it is a standard result of real analysis that there is a \(r>0\) such that \(D(z,r)\subseteq \Omega \) for every \(z\in \Psi \) (with \(r\) independent of \(z\)).
If \(z\in \Psi \) and \(w\in D(z,r/2)\), then \(\overline D(w,r/2)\subset D(z,r)\subseteq \Omega \). By the Cauchy estimates, \(|f_n'(w)|<\frac {2M}{r}\) for all \(n\in \N \).
Choose some \(\varepsilon >0\). Let \(\delta =\min (r/2,\varepsilon r/2M)\). If \(z\), \(\zeta \in \Psi \) with \(|z-\zeta |<\delta \), then \(\zeta \in D(z,r/2)\). Integrating along the straight line segment \(\gamma \) from \(z\) to \(\zeta \), we have that
\begin{align*}|f_n(z)-f_n(\zeta )| &= \left |\oint _\gamma f_n'(w)\,dw\right | \leq \ell (\gamma )\cdot \sup _{\widetilde \gamma } |f_n'| \leq |z-\zeta | \frac {2M}{r} <\delta \frac {2M}{r}\leq \varepsilon \end{align*}for all \(n\in \N \).
Show that if \(\Omega \subseteq \C \) is open, then there exist compact sets \(\Psi _1\subseteq \Psi _2\subseteq \Psi _3\subseteq \dots \) such that \(\cup _m \Psi _m=\Omega \) and such that every compact set \(K\subset \Omega \) is contained in \(\Psi _m\) for some \(m\in \N \). (This property is called \(\sigma \)-compactness.)
Let \(\Psi _m=\{z\in \Omega : D(z,1/m)\subset \Omega \) and \(|z|\leq m\}\). \(\Psi \) is clearly bounded. If \(\{z_n\}_{n=1}^\infty \subset \Psi \) and \(z_n\to z\), then \(|z_n|\to |z|\) and so \(|z|\leq m\). Furthermore, if \(w\in D(z,1/m)\), then \(|z-w|<1/m-\varepsilon \) for some \(\varepsilon >0\). There is a \(z_n\in \Psi _m\) with \(|z-z_n|<\varepsilon \) and so \(w\in D(z_n,1/m)\subseteq \Omega \), and so \(D(z,1/m)\subseteq \Omega \). Thus \(\Psi _m\) is closed.It is clear that \(\Psi _m\subseteq \Psi _{m+1}\) and that \(\Omega =\bigcup _{m=1}^\infty \Psi _m\). Now, suppose \(K\subset \Omega \) is compact. Then \(K\) is bounded, so there is a \(M\in (0,\infty )\) such that \(|z|\leq M\) for all \(z\in K\). Furthermore, because \(K\) is compact and \(\Omega \) is open, there is an \(r>0\) such that \(D(z,r)\subseteq \Omega \) for all \(z\in K\). Let \(m\geq \max (M,1/r)\); then \(K\subseteq \Psi _m\), as desired.
Prove Montel’s theorem, first version.
Find a holomorphic bijection \(f\) from the quarter-plane \(\{x+iy:x,y\in (0,\infty )\}\) to the upper half-plane \(\H \).
Find a holomorphic bijection from the strip \(\{x+iy:x\in \R ,\>y\in (0,\pi )\}\) to the upper half plane.
Find a holomorphic bijection from \(\D \setminus \{0\}\) to \(\C \setminus \overline \D \).
Find a holomorphic bijection from \(\D \) to the strip \(\{x+iy:x\in \R ,\>y\in (0,\pi )\}\).
Find a holomorphic bijection from the quarter-circle \(\{z\in \C :|z|<1,\>\re z>0,\>\im z>0\}\) to the upper half plane.
First, let \(f(z)=z^2\). Then \(f\) is holomorphic and is a bijection from the quarter-circle \(\{z\in \C :|z|<1,\>\re z>0,\>\im z>0\}\) to the half-circle \(\{z\in \C :|z|<1,\>\im z>0\}\).Next, let \(g(z)=\frac {z-1}{iz+i}\). Then \(g\) is a fractional linear transformation, and so \(g\) is one-to-one. By 3630Problem 3630, \(g(\{z\in \C :|z|<1,\>\im z>0\})\) is the quarter-plane \(\{x+iy:x,y\in (0,\infty )\}\). Finally, the function \(f\) sends the quarter plane to the upper half plane. Thus a solution is
\[\varphi (z)=f\circ g\circ f(z)=\biggl (\frac {z^2-1}{iz^2+i}\biggr )^2.\]
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \Omega \). We say that \(f\) is a biholomorphic self-map if it is holomorphic in \(\Omega \) and is a bijection from \(\Omega \) to \(\Omega \).
Let \(f:\C \to \C \). Then \(f\) is a biholomorphic self-map if and only if there are complex numbers \(a\), \(b\in \C \) with \(a\neq 0\) such that that \(f(z)=az+b\) for all \(z\in \C \).
Suppose that \(f:\C \to \C \) is holomorphic and one-to-one. Then \(f\) is linear (and, in particular, is also surjective).
In this problem we prove the more straightforward direction of Theorem 6.1.1. Let \(a\), \(b\in \C \) with \(a\neq 0\). Show that \(f(z)=az+b\) is a biholomorphic self-map of \(\C \).
Let \(X\) and \(Z\) be two topological spaces and let \(f:X\to Z\) be a continuous bijection with continuous inverse. Let \(Y\subseteq X\). Show that \(f(\partial Y)=\partial f(Y)\).
Recall that\begin{equation*}\partial f(Y)=\cl f(Y)\setminus \Int f(Y)=\Bigl (\bigcap _{\substack {f(Y)\subseteq F\\ F\text { closed}}}F \Bigr ) \setminus \Bigl (\bigcup _{\substack {f(Y)\supseteq G\\ G\text { open}}}G \Bigr ).\end{equation*}Because \(f\) and \(f^{-1}\) are continuous, we have that \(E\subseteq X\) is open (respectively closed) if and only if \(f(E)\) is open (respectively closed). Thus
\begin{equation*}\partial f(Y)= \Bigl (\bigcap _{\substack {f(Y)\subseteq F\\ f^{-1}(F)\text { closed}}}F \Bigr ) \setminus \Bigl (\bigcup _{\substack {f(Y)\supseteq G\\ f^{-1}(G)\text { open}}}G \Bigr ).\end{equation*}Because \(f\) is a bijection it provides a one-to-one correspondence between subsets of \(X\) and subsets of \(Z\), and so
\begin{equation*}\partial f(Y)= \Bigl (\bigcap _{\substack {f(Y)\subseteq f(\widetilde F)\\ \widetilde F\text { closed}}}f(\widetilde F) \Bigr ) \setminus \Bigl (\bigcup _{\substack {f(Y)\supseteq f(\widetilde G)\\ \widetilde G\text { open}}}f(\widetilde G) \Bigr ).\end{equation*}Because \(f\) is a bijection it preserves inclusions and commutes with set theoretic operations, and so
\begin{equation*}\partial f(Y)= f\biggl (\Bigl (\bigcap _{\substack {Y\subseteq F\\F\text { closed}}}F \Bigr ) \setminus \Bigl (\bigcup _{\substack {Y\supseteq G\\ G\text { open}}}G \Bigr )\biggr )=f(\partial Y)\end{equation*}as desired.
Let \(f:\D \to \D \) be a biholomorphic self-map. Show that \(f(z)=e^{i\theta } \frac {z-c}{1-\overline c z}\) for some \(c\in \D \) and some \(\theta \in \R \). Hint: Let \(g=f^{-1}\). Compute \(|g'(f(0)) \,f'(0)|\) and use the Schwarz-Pick lemma.
By definition \(f\) is holomorphic. By Problem 5.7, \(g:\D \to \D \) is also holomorphic. Observe that \(h(z)=g(f(z))=z\) for all \(z\in \D \), so \(h'(z)=1\). By the chain rule, \(h'(0)=g'(f(0))\,f'(0)\) so \(|g'(f(0))\,f'(0)|=1\).By the Schwarz-Pick lemma, \(|f'(0)| \leq \frac {1-|f(0)|^2}{1-0^2}=1-|f(0)|^2\). Also, \(|g'(f(0))|\leq \frac {1-|g(f(0))|^2}{1-|f(0)|^2}=\frac {1}{1-|f(0)|^2}\).
If \(|f'(0)|<1-|f(0)|^2\) then \(|g'(f(0))\,f'(0)| < |g'(f(0))|(1-|f(0)|^2)\leq 1\), which is a contradiction. Thus, we must have that \(|f'(0)|=1-|f(0)|^2\).
Again by the Schwarz-Pick lemma, this implies that there is a \(c\in \D \) and a \(\theta \in \R \) such that \(f(z)=e^{i\theta } \frac {z-c}{1-\overline c z}\).
A fractional linear transformation \(f(z)=\frac {az+b}{cz+d}\) is a bijection from \(\H \) to itself if and only if \(a\), \(b\), \(c\), and \(d\) are real numbers and \(ad-bc>0\).
Let \(f:\H \to \H \) be a biholomorphic self-map. Show that \(f\) is a fractional linear transformation (and therefore must be as in Problem 1.10).
Let \(g(z)=\frac {z+1}{iz-i}\) and let \(h(z)=\frac {z-i}{z+i}\); then \(g\) and \(h\) are inverses and by 3583Problem 3583, \(h(\H )=\D \).Thus, the function \(k(z)=h\circ f\circ g\) is a holomorphic bijection from \(\D \) to \(\D \). By the previous problem, we must have that \(k(z)=e^{i\theta } \frac {z-c}{1-\overline c z}\) for some \(\theta \in \R \) and some \(c\in \D \). We therefore have that \(f=g\circ k\circ h\).
Observe in particular that \(f\) is a fractional linear transformation.
We have seen that fractional linear transformations are bimeromorphic self-maps of \(\C \cup \{\infty \}\). Conversely, let \(f:\C \cup \{\infty \}\to \C \cup \{\infty \}\) be a meromorphic bijection (with \(f(z)=\infty \) if \(f\) has a pole at \(z\); because \(f\) is a bijection it has a single pole). Show that \(f\) is a fractional linear transformation. Hint: Does it suffice to prove this in the case that \(f(\infty )=\infty \)?
First, suppose that \(f(\infty )=\infty \). Then \(f:\C \to \C \) must be a bijection and so by Theorem 6.1.1 we have that \(f(z)=az+b\) is a fractional linear transformation.Now, suppose that \(f(w)=\infty \) for some \(w\in \C \). Because \(f\) is a bijection there can be at most one such \(w\). Let \(g(z)=f(w+\frac {1}{z})=f(\frac {wz+1}{z})\). Because \(h(z)=\frac {wz+1}{z}\) is a fractional linear transformation it is a bimeromorphic self-map of \(\C \cup \{\infty \}\). Thus \(g=f\circ h\) is as well and \(g(\infty )=f(w)=\infty \), and so by the above analysis \(g(z)=az+b\) for some \(a\), \(b\in \C \). Then \(f(z)=g(\frac {1}{z-w})\) is a composition of fractional linear transformations, and so is a fractional linear transformation by Theorem 6.3.4.
Let \(\Omega \subseteq \C \) be open and simply connected. Let \(f:\Omega \to \C \) be holomorphic. Show that there exists a holomorphic function \(F:\Omega \to \C \) such that \(F'=f\).
Let \(\gamma :[0,1]\to \Omega \) be a closed curve. By definition of simply connected, \(\gamma \) is homotopic to a constant \(\eta (t)=P\). By 1370Bonus Problem 1370, we may assume the homotopy satisfies the continuity requirements of 1410Problem 1410. By 1410Problem 1410, \(\oint _\gamma f=\oint _\eta f=0\). By 1470Problem 1470, \(f\) has an antiderivative.
A connected open set \(\Omega \subset \C \) is holomorphically simply connected if, whenever \(f:\Omega \to \C \) is holomorphic, there exists a holomorphic function \(F:\Omega \to \C \) with \(F'=f\).
[The Riemann mapping theorem.] Suppose that \(\Omega \subsetneq \C \) is a holomorphically simply connected open set; we emphasize \(\Omega \neq \C \). Then there exists a conformal mapping (holomorphic bijection) \(f:\Omega \to \D \).
Furthermore, for any \(a\in \Omega \), there exists a unique conformal mapping \(f:\Omega \to \D \) such that \(f(a)=0\) and such that \(f'(a)\) is a positive real number.
Assume the Riemann mapping theorem is true. Prove that every holomorphically simply connected region is simply connected.
By 3850Problem 3850, if \(\Omega \) is simply connected then it is holomorphically simply connected. Conversely, let \(\Omega \subseteq \C \) be holomorphically simply connected. If \(\Omega =\emptyset \) or \(\Omega =\C \) then \(\Omega \) is simply connected, so suppose not.Then by the Riemann mapping theorem there is a holomorphic (thus continuous) bijection from \(\Omega \) to \(\D \). Because \(\D \) is simply connected, we must have that \(\Omega \) is as well.
We now begin the proof of Theorem 6.4.2. Suppose that \(\varphi :\D \to \D \) is a conformal mapping, that \(\varphi (0)=0\), and that \(\varphi '(0)>0\) (that is, \(\varphi '(0)\) is a positive real number). Prove that \(\varphi \) is the identity.
By 3820Problem 3820, there is a \(c\in \D \) and a \(\theta \in \R \) such that \(\varphi (z)=e^{i\theta } \frac {z-c}{1-\overline c z}\).But then \(0=\varphi (0)=e^{i\theta } c\), and so we must have that \(c=0\) and so \(\varphi (z)=e^{i\theta } z\). But then \(\varphi '(0)=e^{i\theta }\) is a positive real number, and so we must have that \(e^{i\theta }=1\) and so \(\varphi (z)=z\) for all \(z\in \D \).
Let \(\Omega \subset \C \) be a connected open set and let \(a\in \Omega \). Prove that there is at most one function \(f:\Omega \to \D \) that satisfies the conditions of the Riemman mapping theorem.
If \(\Omega \) is holomorphically simply connected, \(f\) is holomorphic on \(\Omega \), and \(f\neq 0\) on \(\Omega \), then there is some holomorphic function \(h\) on \(\Omega \) such that \(e^h=f\).
Prove Lemma 6.6.4.
Because \(f(z)\neq 0\) for all \(z\in \Omega \), the function \(g(z)=\frac {f'(z)}{f(z)}\) is holomorphic in \(\Omega \). By definition of holomorphically simply connected, there is a function \(H:\Omega \to \C \) such that \(H'(z)=g(z)=\frac {f'(z)}{f(z)}\).Choose some \(z_0\in \Omega \) and let \(C\in \C \) be such that \(e^{H(z_0)+C}=f(z_0)\). Because \(f(z_0)\neq 0\), some such \(C\) must exist. Let \(h(z)=H(z)+C\); we still have that \(h'(z)=\frac {f'(z)}{f(z)}\).
Now, let \(g(z)={f(z)}{e^{-h(z)}}\). Then \(g(z_0)=1\). We compute \(g'(z)={f'(z) e^{h(z)}-f(z) e^{h(z)}h'(z)}=0\) because \(f(z)\,h'(z)=f'(z)\). Because \(\Omega \) is connected, we must have that \(g\) is a constant, so \(g(z)=1\) for all \(z\in \Omega \); thus \(f(z)=e^{h(z)}\) for all \(z\in \Omega \).
Let \(\Omega =\C \setminus \{x+0i:x\leq 0\}\) be the complex plane minus a slit. Let \(f(z)=z^2\) be holomorphic on \(\Omega \).
If \(z\in \Omega \), then there is a unique positive real number \(r\) and a unique real number \(\theta \) with \(-\pi <\theta <\pi \) such that \(z=re^{i\theta }\). Define \(h(z)=h(re^{i\theta })=2\ln r+2i\theta \). It is elementary to check that \(e^h=f\).Then \(f(i)=-1=f(-i)\), but \(h(i)=i\pi \neq -i\pi =h(-i)\). For any possible branch of log, \(\log f(i)log f(-i)\) because \(\log f(i)=\log -1=\log f(-i)\); thus, we cannot find a branch of \(\log \) such that \(h=\log \circ f\).
If \(\Omega \) is holomorphically simply connected, \(f\) is holomorphic on \(\Omega \), and \(f\neq 0\) on \(\Omega \), then there is some holomorphic function \(k\) on \(\Omega \) such that \(k^2=f\).
Prove Corollary 6.6.5.
We may simply take \(k=e^{(1/2) h}\), where \(h\) is as in Lemma 6.6.4.
Suppose that \(\Omega \subset \C \) is open and that for some \(Q\in \C \) and \(r>0\), we have that \(\Omega \cap D(Q,r)=\emptyset \). Find a one-to-one holomorphic function \(g:\Omega \to \D \). (\(g\) need not be a bijection.)
Let \(g(z)=\frac {r/2}{z-Q}\).Since \(Q\notin \Omega \) we have that \(g\) is well defined on \(\Omega \), and by inspection \(g\) is one-to-one and holomorphic on \(\C \setminus \{Q\}\).
Now, if \(w\in \Omega \) then \(w\notin D(Q,r)\), and so \(|w-Q|\geq r\). Thus \(|g(w)|\leq 1/2\) and so \(g(\Omega )\subset \D \), as desired.
Suppose that \(\Omega \) is holomorphically simply connected and that \(P\notin \Omega \) for some \(P\in \C \). Using the function \(h\) of 3880Problem 3880, show that there exists a one-to-one holomorphic function \(g:\Omega \to \D \). [This problem will be assigned as homework. Note that your book does this exercise using the function \(k\) of 3900Problem 3900.]
Let \(\Omega \subsetneq \C \) be holomorphically simply connected with \(a\in \Omega \). Let \(\mathcal {F}\) be the set of all functions \(f\) such that
To prove the Riemann mapping theorem, what do we need to prove about \(\mathcal {F}\)?
Show that \(\mathcal {F}\) is nonempty.
Let \(R=\sup \{f'(a):f\in \mathcal {F}\}\). Show that \(0<R<\infty \).
By the previous problem there is a \(g\in \mathcal {F}\). By definition of \(\mathcal {F}\) we have that \(g'(a)>0\), and so \(R\geq g'(a)>0\).We now turn to the proof that \(R\) is finite. Because \(\Omega \) is open, there is a \(r>0\) such that \(D(a,r)\subseteq \Omega \).
By the Cauchy estimates (Theorem 3.4.1), if \(f\in \mathcal {F}\), then
\begin{equation*}|f'(a)|\leq \frac {2}{r}\sup _{\partial D(a,r/2)}|f|.\end{equation*}But \(f(\Omega )\subseteq \D \) and so \(|f(z)|<1\) for all \(z\in \Omega \supseteq D(a,r)\); thus \(|f'(a)|\leq 2/r\) for all \(f\in \mathcal {F}\) and so \(R\leq 2/r\).
Show that there is a function \(f\in \mathcal {F}\) such that \(f'(a)=R\).
If \(f\in \mathcal {F}\) and \(f'(a)=R\), then \(f:\Omega \to \D \) is surjective.
Let \(0<r<1\). Let \(W=\D \setminus (-1,-r]=\{x+iy:x^2+y^2<1\) and either \(y\neq 0\) or \(x>-r\}\) be the unit disc with a slit removed; then \(0\in W\subsetneq \D \). Let
where \(\phi _c\) is as in 3390Lemma 3390 and where \(\sqrt {re^{i\theta }}=\sqrt {r}e^{i\theta /2}\) if \(0<r<\infty \) and \(-\pi <\theta <\pi \). Show that
Note: You must prove \(\psi '(0)>1\); this is much harder than proving \(\psi '(0)>0\)!
Recall that \(\phi _{-r}\) is a bijection from \(\D \) to itself. We compute that \(\phi _{-r}(r)=0\), \(\phi _{-r}(-1)=-1\), \(\phi _{-r}(1)=1\), and \(\phi _{-r}(0)=r\). Thus by Theorem 6.3.4 and Theorem 6.3.7, \(\phi _{-r}\) is a bijection from \(\R \cup \{\infty \}\) to itself; furthermore it is continuous in the metric of 2930Problem 2930, and so we must have that \(\phi _{-r}\) maps \([-1,-r]\) to \([-1,0]\). Thus \(\Omega =\phi _{-r}(W)=\D \setminus (-1,0]\).
By definition of \(\sqrt {\>}\), we have that \(\sqrt {z}\) exists for all \(z\in \Omega \) and is holomorphic in \(\Omega \) by 2680Problem 2680. Observe that \(\sqrt {\>}\) is also one-to-one. Thus \(g(z)=\sqrt {\phi _{-r}(z)}\) is holomorphic in \(W\). Furthermore, \(g(w)\) is the right half circle and thus is contained in \(\D \):
Finally \(\phi _{\sqrt {r}}\) is holomorphic and injective in \(\D \), and so \(\psi =\phi _{\sqrt {r}}\circ g\) is holomorphic and injective in \(W\).
We compute \(\varphi _{-r}(0)=r\), \(\sqrt {\varphi _{-r}(0)}=\sqrt {r}\), and \(\varphi _{\sqrt {r}}(\sqrt {r}=0\), so \(\psi (0)=0\).
Finally, by the chain rule, 2680Problem 2680, and 3440Problem 3440,
\begin{align*} \varphi '(0) &= \varphi _{\sqrt {r}}'(\sqrt {r})\cdot \frac {1}{2\sqrt {r}}\cdot \varphi _{-r}'(0) \\&= \frac {1-r}{(1-r)^2} \frac {1}{2\sqrt {r}} (1-r^2) \\&=\frac {(1+r)/2}{\sqrt {1\cdot r}} .\end{align*}Because \(r\) and \(1\) are unequal positive real numbers, by the arithmetic-geometric mean inequality this quantity is greater than \(1\).
Let \(W\subsetneq \D \) be open and holomorphically simply connected with \(0\in W\). Show that there exists a \(\psi \) such that
Hint: The construction will be similar to the previous problem with Corollary 6.6.5 in place of the explicit square root function. Note: You must prove \(\psi '(0)>1\); this is much harder than proving \(\psi '(0)>0\)!
Let \(P\in \D \setminus W\). By assumption some such \(P\) exists. Thus \(\phi _P:W\to \D \) is holomorphic, and because \(\phi _P(P)=0\), \(P\in \D \setminus W\), and \(\phi _P\) is a bijection from \(\D \) to itself, we have that \(\phi _P\neq 0\) in \(W\). Thus by Corollary 6.6.5 there is a holomorphic function \(g:W\to \C \) such that \(g(z)^2=\phi _P(z)\) for all \(z\in W\). It is left as an exercise to the student that \(g(W)\subseteq \D \). Let \(\psi =e^{i\theta } \phi _b(g(z))\) where \(b=g(0)\) and where \(\theta \in \R \). It is left as an exercise to the student to show that we may choose \(\theta \) such that \(\psi \) satisfies the desired conditions.
Let \(\Omega \subseteq \C \) be open and holomorphically simply connected and let \(f:\Omega \to \C \) be a holomorphic injection. Show that \(f(\Omega )\) is also open and holomorphically simply connected.
We begin by showing that \(f(\Omega )\) is open. Let \(z\in f(\Omega )\). Then there is some \(P\in \Omega \) such that \(f(P)=z\). Because \(\Omega \) is open, there is an \(r>0\) such that \(D(P,r)\subseteq \Omega \) and so \(f(D(P,r))\subseteq f(\Omega )\). By the Open Mapping Theorem (Theorem 5.2.1), \(f(D(P,r))\) is either a single point or open; because \(f\) is injective we have that \(f(D(P,r))\) must be open. Thus for every \(z\in f(\Omega )\) there is an open set \(U\) with \(z\in U\subseteq f(\Omega )\); thus \(f(\Omega )\) must be open.Now, let \(g:f(\Omega )\to \C \) be a holomorphic function. Then \(g\circ f\) is a holomorphic function from \(\Omega \) to \(\C \) and so is \(f'\), so their product \(h(z)=g(f(z))\cdot f'(z)\) is also holomorphic. Because \(\Omega \) is holomorphically simply connected, we have that there is some \(H:\Omega \to \C \) holomorphic such that \(H'(z)=h(z)\).
Recall from Problem 5.7 that \(f^{-1}\) is a holomorphic function \(f^{-1}:f(\Omega )\to \Omega \). Let \(G(z)=H(f^{-1}(z))\). By the chain rule, \(1=f'(f^{-1}(z))\cdot (f^{-1})'(z)\) and \(G'(z)= H'(f^{-1}(z))\cdot (f^{-1})'(z) = g(f(f^{-1}(z)))\cdot f'(f^{-1}(z))\cdot \frac {1}{f'(f^{-1}(z))}=g(z)\), as desired.
(While the function \(g\circ f\) indeed has a holomorphic antiderivative, it is very difficult to derive a holomorphic antiderivative for \(g\) alone from the holomorphic antiderivative for \(g\circ f\).)
Prove Claim 6.7.3 by showing that if \(f\in \mathcal {F}\) is not surjective, then there is a \(g\in \mathcal {F}\) such that \(f'(a)<g'(a)\).
Let \(f\in \mathcal {F}\) and suppose that \(W=f(\Omega )\subsetneq \D \). By 3990Problem 3990 we have that \(W\) is also open and holomorphically simply connected. Because \(f(a)=0\) we have that \(0\in W\).Therefore, by 3980Problem 3980, there is a holomorphic injection \(\psi :W\to \D \) such that \(\psi (0)=0\) and \(\psi '(0)>1\).
Let \(g=\psi \circ f\). Because \(\psi \) is defined on \(W=f(\Omega )\), \(g\) is defined on \(\Omega \). Then
- \(g\) is holomorphic on \(\Omega \) (as the composition of two holomorphic functions \(\psi \) and \(f\)),
- \(g\) is one-to-one (as the composition of two one-to-one functions),
- \(g(\Omega )=\psi (f(\Omega ))=\psi (W)\subseteq \D \),
- \(g(a)=\psi (f(a))=\psi (0)=0\),
- \(g'(a)=(\psi \circ f)'(a)=\psi '(f(a))\cdot f'(a)=\psi '(0)\cdot f'(a)\) by 1120Problem 1120. Thus \(g'(a)\) is a positive real number (as a product of two positive real numbers).
Thus \(g\in \mathcal {F}\). Furthermore, \(g'(a)=\psi '(0)\cdot f'(a)>f'(a)\) because \(f'(a)>0\) and \(\psi '(0)>1\). This completes the proof.
Let \(\Omega \subsetneq \C \) be holomorphically simply connected with \(a\in \Omega \). Let \(\mathcal {F}\) be the set of all functions \(f\) such that
\(\mathcal F\) is nonempty.
\(0<\sup \{g'(a):g\in \mathcal {F}\}<\infty \).
(Claim 6.7.3.) If \(f\in \mathcal {F}\) and \(f'(a)=\sup \{g'(a):g\in \mathcal {F}\}\), then \(f:\Omega \to \D \) is onto.
Prove that there is a function \(f\in \mathcal {F}\) with \(f'(a)=\sup \{g'(a):g\in \mathcal {F}\}\). (This proves the Riemann mapping theorem.)
By definition of supremum, if \(n\in \N \), then there is a \(f_n\in \mathcal {F}\) such that \(f_n'(a)>\sup \{g'(a):g\in \mathcal {F}\}-\frac {1}{n}\). Observe that \(\mathcal {F}\) is a family of holomorphic functions with a common domain \(\Omega \) whose range is contained in \(\D \); thus if \(f\in \mathcal {F}\) then \(\sup _\Omega |f|\leq 1\). Thus, by Montel’s theorem, \(\mathcal {F}\) is a normal family. Thus there is subsequence \(\{f_{n_k}\}_{k=1}^\infty \) of \(\{f_n\}_{n=1}^\infty \) which converges normally. Let \(f=\lim _{k\to \infty } f_{n_k}\).We claim that \(f\in \mathcal {F}\) with \(f'(a)=\sup \{g'(a):g\in \mathcal {F}\}\).
By Theorem 3.5.1, \(f\) is holomorphic on \(\Omega \). By definition of limit \(f(a)=\lim _{k\to \infty } f_{n_k}(a)=0\). By Corollary 3.5.2, \(f'(a)=\lim _{k\to \infty } f_{n_k}'(a)=\sup \{g'(a):g\in \mathcal {F}\}\). In particular \(f'(a)>0\), and so \(f\) is not a constant.
If \(z\in \Omega \), then \(|f(z)|=\lim _{k\to \infty } |f_{n_k}(z)|\leq 1\) because \(f_{n_k}(\Omega )\subseteq \D \). By the maximum modulus principle (Theorem 5.4.2), we must have that \(|f(z)|<1\) for all \(z\in \Omega \), and thus \(f(\Omega )\subseteq \D \).
By 3360Problem 3360, \(f\) is injective. This completes the proof.
Harmonic function. We say that \(u\) is harmonic in a domain \(\Omega \subseteq \C \) if \(u\) is \(C^2\) in \(\Omega \) and if \(\frac {\partial ^2 u}{\partial x^2}+\frac {\partial ^2 u}{\partial y^2}=0\) in \(\Omega \).
Let \(\Omega \subseteq \C \) be open and let \(F:\Omega \to \R \) be a continuous function. Suppose that, for all compact subsets \(K\) of \(\Omega \), and all functions \(\phi :\Omega \to \R \) that are smooth (meaning \(C^\infty \)) and satisfy \(\phi (z)=0\) for all \(z\in \Omega \setminus K\), we have that \(\int _\Omega F\,\Delta \phi =0\). Then \(F\) is harmonic in \(\Omega \).
If \(\Omega \subseteq \C \) is open and \(f:\Omega \to \C \), then \(f\) is harmonic if and only if both \(u=\re f\) and \(v=\im f\) are harmonic.
Let \(\Omega \subseteq \C \) be open and let \(u\in C^2(\Omega )\). Show that the following are equivalent:
Let \(\Omega \subseteq \C \) be open and let \(u\in C^2(\Omega )\).Recall that \(\frac {\partial }{\partial z} = \frac {1}{2}\frac {\partial }{\partial x}+\frac {1}{2i}\frac {\partial }{\partial y}\) and \(\frac {\partial }{\partial \bar z} = \frac {1}{2}\frac {\partial }{\partial x}-\frac {1}{2i}\frac {\partial }{\partial y}\).
Then
\begin{align*} \frac {\partial }{\partial z}\left (\frac {\partial }{\partial \bar z} u\right ) &= \frac {\partial }{\partial z} \left ( \frac {1}{2}\frac {\partial u}{\partial x} -\frac {1}{2}\frac {\partial u}{\partial y} \right ) \\&=\frac {1}{2} \frac {\partial }{\partial x}\left ( \frac {1}{2}\frac {\partial u}{\partial x} -\frac {1}{2i}\frac {\partial u}{\partial y} \right ) +\frac {1}{2i}\frac {\partial }{\partial y}\left ( \frac {1}{2}\frac {\partial u}{\partial x} -\frac {1}{2}\frac {\partial u}{\partial y} \right ) \\&= \frac {1}{4}\frac {\partial ^2 u}{\partial x^2} +\frac {1}{4} \frac {\partial ^2 u}{\partial y^2} -\frac {1}{4i} \frac {\partial ^2 u}{\partial x\partial y} +\frac {1}{4i} \frac {\partial ^2 u}{\partial y\partial x}. \end{align*}By equality of mixed partials the final two terms cancel and we see that \(u\) is harmonic if and only if \(\frac {\partial }{\partial z} \left (\frac {\partial u}{\partial \bar z}\right )=0\). Because \(\frac {\partial }{\partial z}\) and \(\frac {\partial }{\partial \bar z}\) commute, we see that \(u\) is harmonic if and only if \(\frac {\partial }{\partial \bar z} \left (\frac {\partial u}{\partial z}\right )=0\).
Suppose that \(\Omega \subseteq \C \) is open and that \(u\), \(v:\Omega \to \C \) are both harmonic. Let \(\alpha \), \(\beta \in \C \). Show that \(\alpha u+\beta v\) is also harmonic.
If \(u\) is a real-valued harmonic function on a connected open set, and if \(u^2\) is also harmonic, then \(u\) is a constant.
If \(u\) is a complex-valued harmonic function on a connected open set \(\Omega \), and if \(u^2\) is also harmonic, then \(u\) is either holomorphic or conjugate-holomorphic (meaning that either \(u\) or \(\overline u\) is holomorphic, or, equivalently, either \(\p [u]{z}\equiv 0\) or \(\p [u]{\bar z}\equiv 0\) in \(\Omega \)).
Prove that if \(F\) is holomorphic in an open set \(\Omega \) and \(u=\re F\) then \(u\) is harmonic.
Because \(F'=\frac {\partial }{\partial z} F\) is also holomorphic, we have that \(0=\frac {\partial }{\partial \bar z} F' = \frac {\partial }{\partial \bar z}\frac {\partial }{\partial z} F=\frac {\partial }{\partial z} \frac {\partial }{\partial \bar z} F\). Thus \(F\) is harmonic.So
\begin{equation*}0=\frac {\partial ^2 F}{\partial x^2}+\frac {\partial ^2 F}{\partial y^2} =\left (\frac {\partial ^2 \re F}{\partial x^2}+\frac {\partial ^2 \re F}{\partial y^2}\right ) +i\left (\frac {\partial ^2 \im F}{\partial x^2}+\frac {\partial ^2 \im F}{\partial y^2}\right ) .\end{equation*}Because the two quantities \(\left (\frac {\partial ^2 \re F}{\partial x^2}+\frac {\partial ^2 \re F}{\partial y^2}\right )\) and \(\left (\frac {\partial ^2 \im F}{\partial x^2}+\frac {\partial ^2 \im F}{\partial y^2}\right )\) are both real, they must both be zero and \(\re F\) and \(\im F\) are both harmonic.
Prove that if \(F\) is holomorphic in an open set \(\Omega \) and \(v=\im F\) then \(v\) is harmonic.
We have that \(G=-iF\) is holomorphic. But \(\re G = \im F=v\) and \(\re G\) is harmonic by the previous problem.
If \(u\) is real-valued and harmonic in a simply connected open set \(\Omega \), then there is a holomorphic function \(f\) such that \(\re f=u\).
Prove Lemma 7.1.4.
Observe that \(\frac {\partial }{\partial \bar z} (\frac {\partial }{\partial z} u)=0\). Thus \(\frac {\partial }{\partial z} u\) is holomorphic in \(\Omega \). Because \(\Omega \) is simply connected, by 3850Problem 3850 it is holomorphically simply connected, and so every holomorphic function has a holomorphic antiderivative. Thus, there is a holomorphic function \(F\) such that \(\frac {\partial }{\partial z} F=\frac {\partial }{\partial z} u\). Let \(f=2F-2F(z_0)+u(z_0)\), where \(z_0\) is some fixed point in the domain.We compute that
\begin{align*} \p {x}u-i\p {y}u &=2\p {z}u=2\p {z}F=\p {z}f .\end{align*}By Proposition 1.4.3, we have that \(\p [f]{z}=\p [f]{x}\), and so
\begin{align*} \p {x}u-i\p {y}u &=\p {x}f=\p {x}(\re f)+i\p {x}(\im f) .\end{align*}Again by Proposition 1.4.3, we have that \(\p [f]{z}=-i\p [f]{y}\), and so
\begin{align*} \p {x}u-i\p {y}u &=-i\p {y}f=-i\p {y}(\re f)+\p {y}(\im f) .\end{align*}Equating the real and imaginary parts, we see that \(\nabla u=\nabla (\re f)\). Since \(u=\re f\) at a point in the (connected) domain, we must have that they are equal everywhere.
If \(\Omega \subseteq \C \) is open and \(u:\Omega \to \R \) is harmonic, then \(u\) is smooth.
Prove Corollary 7.1.3.
Let \(u\) be harmonic in an open set \(\Omega \). Let \(D(P,r)\subseteq \Omega \) for some \(P\in \C \) and some \(r>0\). Then by 4050Problem 4050, there is some function \(f\) holomorphic in \(D(P,r)\) such that \(u=\re f\) in \(D(P,r)\).By Theorem 3.1.1, we have that \(f\) is smooth (infinitely differentiable) in \(D(P,r)\). Therefore, \(u=\re f\) is infinitely differentiable in \(D(P,r)\). Since this is true in every disc contained in \(\Omega \), \(u\) is smooth throughout \(\Omega \).
Let \(u\) and \(v\) be two real-valued functions. If \(F=u+iv\) is holomorphic, then we say that \(v\) is a harmonic conjugate of \(u\).
Suppose that \(v_1\) and \(v_2\) are both conjugates of the (real harmonic) function \(u\). What can you say about \(v_1\) and \(v_2\)?
We can say that \(v_1-v_2\) is locally constant, that is, constant on any connected component of the domain of \(u\).
Let \(u\) be a harmonic function. Suppose that \(v\) is a harmonic conjugate of \(u\). Is \(u\) also a harmonic conjugate of \(v\)?
No, but \(-u\) is a harmonic conjugate of \(v\).
(The maximum principle for harmonic functions.) If \(\Omega \subseteq \C \) is open and connected, if \(u:\Omega \to \R \) is harmonic, and if there is a \(P\in \Omega \) such that \(u(P)\geq u(z)\) for all \(z\in \Omega \), then \(u\) is constant in \(\Omega \).
Prove the maximum principle for harmonic functions.
Let \(M=u(P)\) and let \(E=u^{-1}(\{M\})=\{z\in \Omega :u(z)=M\}\). Then \(E\subseteq \Omega \) is not empty because \(P\in E\). The set \(\{M\}\) is closed, so \(E\) must also be (relatively) closed in \(\Omega \) because \(u\) is continuous.Let \(Q\in E\). Because \(\Omega \) is open, there is an \(r>0\) such that \(D(Q,r)\subseteq \Omega \). By 4050Problem 4050, there is a \(f:D(Q,r)\to \C \) that is holomorphic in \(\Omega \) such that \(u=\re f\) in \(D(Q,r)\). Let \(h=e^f\). Then \(|h|=e^u\), and because the exponential function is strictly increasing on the reals and \(u(Q)=u(P)\geq u(z)\) for all \(z\in D(Q,r)\), we have that \(|h|\) attains a maximum at \(Q\). Thus \(h\) must be constant on \(D(Q,r)\). But \(u=\ln |h|\), and so \(u\) is also constant in \(D(Q,r)\). Since \(Q\in E\), we have \(u(Q)=M\) and so \(u(z)=M\) for all \(z\in D(Q,r)\); thus \(D(Q,r)\subseteq E\). This is true for all \(Q\in E\), and so \(E\) is open.
Because \(\Omega \) is connected and \(E\subseteq \Omega \) is nonempty, open, and relatively closed, we must have that \(E=\Omega \) and so \(u\) is constant in \(\Omega \).
State and prove the minimum principle and corollaries involving the values of \(u\) on \(\partial \Omega \).
The minimum principle is as follows:If \(\Omega \subseteq \C \) is open and connected, if \(u:\Omega \to \R \) is harmonic, and if there is a \(P\in \Omega \) such that \(u(P)\leq u(z)\) for all \(z\in \Omega \), then \(u\) is constant in \(\Omega \).
It may be proven by noting that, if \(u\) is harmonic, then so is \(v=-u\), and if \(u(P)\leq u(z)\) then \(v(P)\geq v(z)\).
Here is the corollary:
Let \(\Omega \subset \C \) be nonempty, open and bounded. Let \(u:\overline \Omega \to \R \) be a continuous function such that \(u\) is harmonic in \(\Omega \). Then there are points \(z_0\) and \(z_1\) in \(\partial \Omega \) such that \(u(z_0)\leq u(z)\leq u(z_1)\) for all \(z\in \overline \Omega \). Furthermore, if \(\Omega \) is connected then either \(u(z_0)=u(z_1)=u(z)\) for all \(z\in \overline \Omega \) or \(u(z_0)<u(z)<u(z_1)\) for all \(z\in \Omega \).
It may be proven by recalling the well known fact that a continuous function on a compact set (in particular, on any closed and bounded subset of \(\C \)) attains its maximum and minimum.
(The mean value property.) If \(u\) is harmonic in a neighborhood of \(\overline D(P,r)\), then
Prove the mean value property.
Let \(\Omega \supset \overline D(P,r)\) be the indicated neighborhood. By a standard real analysis argument, there is a \(R>r\) such that \(\overline D(P,r)\subset D(P,R)\subseteq \Omega \).Because \(D(P,R)\) is simply connected and \(u\) is harmonic in \(\Omega \supseteq D(P,R)\), by Lemma 7.1.4 there is a holomorphic function \(f:D(P,R)\to \C \) such that \(u=\re f\) in \(D(P,R)\). By the Cauchy integral formula,
\begin{equation*}f(P)=\frac {1}{2\pi i}\oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -P}\,d\zeta .\end{equation*}We use the standard parameterization \(\gamma (t)=P+re^{it}\) and see that, by the definition of line integral,
\begin{align*} f(P)&=\frac {1}{2\pi i}\oint _{\gamma } \frac {f(\zeta )}{\zeta -P}\,d\zeta =\frac {1}{2\pi i}\int _0^{2\pi } \frac {f(\gamma (t))}{\gamma (t)-P}\,\gamma '(t)\,dt \\&=\frac {1}{2\pi i}\int _0^{2\pi } \frac {f(P+re^{it})}{re^{it}}\,ire^{it}\,dt =\frac {1}{2\pi }\int _0^{2\pi } f(P+re^{it})\,dt.\end{align*}But by definition of the integral of a complex function over a real interval,
\begin{align*}u(P)&=\re f(P) = \re \frac {1}{2\pi }\int _0^{2\pi } f(P+re^{it})\,dt \\&=\frac {1}{2\pi }\int _0^{2\pi } \re f(P+re^{it})\,dt =\frac {1}{2\pi }\int _0^{2\pi } u(P+re^{it})\,dt.\end{align*}
Suppose that \(u\) is harmonic in \(D(P,r)\) and continuous on \(\overline D(P,r)\) (without necessarily being harmonic in any larger set). Is the mean value property still valid?
Yes. Let \(0<\rho <r\). By the previous problem,\begin{equation*}u(P)=\frac {1}{2\pi } \int _0^{2\pi } u(P+\rho e^{i\theta })\,d\theta .\end{equation*}Thus,
\begin{equation*}u(P)=\frac {1}{2\pi } \lim _{\rho \to r^-}\int _0^{2\pi } u(P+\rho e^{i\theta })\,d\theta .\end{equation*}Because \(u\) is continuous on the compact set \(\overline D(P,r)\), it is uniformly continuous. Choose \(\varepsilon >0\). There is a \(\delta >0\) such that if \(z\), \(w\in \overline D(P,r)\) then \(|u(z)-u(w)|<\varepsilon \).
In particular, if \(\rho >r-\delta \) then \(|re^{i\theta }-\rho e^{i\theta }|=r-\rho <\delta \) and so \(|u(re^{i\theta })-u(\rho e^{i\theta })|<\varepsilon \).
If we let \(u_\rho (\theta )=u(P+\rho e^{i\theta })\), then \(u_\rho \to u_r\) uniformly as \(\rho \to r\) from the left, and so by 750Memory 750, we have that
\begin{equation*}\int _0^{2\pi } u_r(\theta )\,d\theta =\lim _{\rho \to r^-} \int _0^{2\pi } u_\rho (\theta )\,d\theta \end{equation*}and so
\begin{equation*}\frac {1}{2\pi } \int _0^{2\pi } u(P+r e^{i\theta })\,d\theta =\lim _{\rho \to r^-} u(P)=u(P),\end{equation*}as desired.
Let \(\Omega \), \(W\subseteq \C \) be open sets, let \(\psi :\Omega \to W\) be holomorphic, and let \(u:W\to \R \) be harmonic. Then \(u\circ \psi \) is harmonic.
Prove Lemma 7.3.2.
Let \(P\in \Omega \). We will show that \(u\circ \psi \) is holomorphic in some open neighborhood of \(P\).Because \(W\) is open and \(\psi (P)\in W\) there is a \(\varepsilon >0\) such that \(D(\psi (P),\varepsilon )\subseteq W\). By Lemma 7.1.4 there is a holomorphic function \(f:D(\psi (P),\varepsilon )\to \C \) such that \(u=\re f\) in \(D(\psi (P),\varepsilon )\).
Because \(\psi \) is holomorphic it is continuous, and so there is a \(\delta >0\) such that \(\psi (D(P,\delta ))\subset D(\psi (P),\varepsilon )\).
Then \(\psi :D(P,\delta )\to D(\psi (P),\varepsilon )\) and \(f:D(\psi (P),\varepsilon )\to \C \) are both holomorphic, so by Problem 1.49 \(f\circ \psi \) is holomorphic in \(D(P,\delta )\).
But \(u=\re f\) in \(D(\psi (P),\varepsilon )\) and so \(u\circ \psi =\re (f\circ \psi )\) in \(D(P,\delta )\), and so \(u\circ \psi \) is harmonic in \(D(P,\delta )\) by 4040Problem 4040. Because \(P\in \Omega \) was arbitrary and harmonicity is a local property, this suffices to show that \(u\circ \psi \) is harmonic in \(\Omega \).
Let \(P(z,\zeta )=\frac {\abs {\zeta }^2-\abs {z}^2}{2\pi \abs {\zeta -z}^2}\); \(P\) is called the Poisson kernel.
(The Poisson integral formula.) Suppose that \(u\) is harmonic in \(D(0,R)\supset \overline \D \) for some \(R>1\). If \(w\in \D \), then
Prove the Poisson integral formula.
Let \(v=u\circ \phi _{-w}\), so \(v(0)=u(w)\). Then\begin{align*} u(w)&=v(0)=\frac {1}{2\pi } \int _0^{2\pi } v(e^{i\theta })\,d\theta \\&=\frac {1}{2\pi } \int _0^{2\pi } u(\phi _{-w}(e^{i\theta }))\,d\theta \\&=\frac {1}{2\pi } \oint _{\partial \D } \frac {1}{i\zeta } u(\phi _{-w}(\zeta ))\,d\zeta . \end{align*}Recall that \(\phi _w\) and \(\phi _{-w}\) are inverses. Multiplying and dividing by \(\phi _{-w}'(\zeta )\), and then replacing most occurrences of \(\zeta \) by \(\phi _w(\phi _{-w}(\zeta ))\), we see that
\begin{align*} u(w) &=\frac {1}{2\pi } \oint _{\partial \D } \frac {u(\phi _{-w}(\zeta )) }{i\phi _w(\phi _{-w}(\zeta ))\,\phi _{-w}'(\phi _w(\phi _{-w}(\zeta )))} \phi _{-w}'(\zeta )\,d\zeta .\end{align*}This is of the form \(\oint _\gamma F(\phi _{-w}(\zeta )) \phi _{-w}'(\zeta ) \,d\zeta \) for a continuous function \(F\), where \(\gamma \) is the standard parameterization of \(\partial \D \), and so we may use a change of variables as in 1060Problem 1060. This yields that
\begin{align*} u(w) &=\frac {1}{2\pi } \oint _{\phi _{-w}\circ \gamma } \frac {u(z) }{i\phi _w(z)\,\phi _{-w}'(\phi _w(z))} dz. \end{align*}Recall that \(\frac {1}{\phi _{-w}'(\phi _w(z))} = \phi _w'(z)\), so
\begin{align*} u(w) &=\frac {1}{2\pi } \oint _{\phi _{-w}\circ \gamma } \frac {u(z) }{i\phi _w(z)} \phi _w'(z)dz . \end{align*}\(\phi _{-w}\circ \gamma \) is a \(C^1\) bijection \([0,2\pi )\to \partial \D \). So it is either a single counterclockwise or a single clockwise parameterization of \(\partial \D \). Thus
\begin{align*} u(w) &=\pm \frac {1}{2\pi } \oint _{\gamma } \frac {u(z) }{i\phi _w(z)} \phi _w'(z)dz \\&=\pm \frac {1}{2\pi } \int _0^{2\pi } \frac {u(e^{i\psi }) }{i\phi _w(e^{i\psi })} \phi _w'(e^{i\psi })\,ie^{i\psi }\,d\psi \end{align*}where \(\pm \) depends on \(\phi _w\circ \gamma \) but not on \(u\). Recall \(\phi _w'(z)=\frac {1-|w|^2}{(1-\overline w z)^2}\). Sufficient algebra yields
\begin{equation*}u(w)=\pm \frac {1}{2\pi } \int _0^{2\pi } u(e^{i\psi }) \frac {1-|w|^2}{|e^{i\psi }-w|^2}\,d\psi .\end{equation*}Considering \(u=1\) yields that \(\pm =+\).
We use Theorem 7.3.3 and a change of variables to see that\begin{equation*}u(z) =\frac {1}{2\pi }\int _0^{2\pi } u(P+re^{i\theta }) \frac {r^2-|z-P|^2}{|P+re^{i\theta }-z|^2}\,d\theta \end{equation*}if \(u\) is harmonic in \(D(P,R)\) for some \(R>r\).
In particular, if \(u\) is harmonic in \(D(P,r)\) and continuous on \(\overline D(P,r)\) then
\begin{equation*}u(z) =\frac {1}{2\pi }\int _0^{2\pi } u(P+\varrho e^{i\theta }) \frac {\varrho ^2-|z-P|^2}{|P+\varrho e^{i\theta }-z|^2}\,d\theta \end{equation*}whenever \(|z-P|<\varrho <r\).
Because \(\overline D(P,r)\) is compact, if \(u\) is continuous then it is uniformly continuous. Taking the limit as \(\varrho \to r^-\) and applying 750Memory 750 completes the proof.
Let \(f\) be holomorphic in \(D(P,r)\) and continous on \(\overline D(P,r)\). Then \(f(z)=\frac {1}{2\pi i}\oint _\gamma \frac {f(\zeta )}{\zeta -z}\,d\zeta \) for all \(z\in D(P,r)\).
Let \(f\) be continuous on \(\partial D(P,r)\). Define \(F\) by \(F(z)=\frac {1}{2\pi i}\oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta \) for all \(z\in D(P,r)\). Then \(F\) is \(C^1\) and holomorphic in \(D(P,r)\).
It is not necessarily true that \(\lim _{w\to z} F(w)=f(z)\) for \(z\in \partial D(P,r)\).
Let \(f:\partial \D \to \R \) be continuous. If \(z\in \D \), define
Then \(u\) is harmonic in \(\D \), and \(\lim _{z\to e^{i\theta }} u(z)=f(e^{i\theta })\) for all \(\theta \in [0,2\pi ]\). In particular, if we define \(u(z)=f(z)\) for all \(z\in \partial \D \), then \(u\) is continuous on \(\overline \D \).
Show that \(p(z)=P(z,\zeta )\) is harmonic on \(\C \setminus \{\zeta \}\); in particular, if \(\zeta =e^{i\theta }\) then \(p(z)\) is harmonic in \(\D \). Hint: Write \(p\) as the real part of a holomorphic function and apply 4040Problem 4040.
In this problem we begin the proof of Theorem 7.3.4. Let \(u\) be as in Theorem 7.3.4. Prove that \(u\) is harmonic in \(\D \).
Define \(F(\psi ,x,y)=f(e^{i\psi })P(x+iy,e^{i\psi }) =f(e^{i\psi })\frac {1-x^2-y^2}{|e^{i\psi }-x-iy|^2}\).Observe that \(F\) is continuous in \(\psi \) and twice continuously differentiable in both \(x\) and \(y\) in the region \(\{(\psi ,x,y):\psi \in \R ,\>x^2+y^2<1\}\). Observe that for fixed \(\psi \) and \(y\) (or \(\psi \) and \(x\)) this region contains a set of \(x\)-values (or \(y\)-values) that is open in \(\R \).
By 770Problem 770, this implies that for \((\psi ,x,y)\) in the same region,
\begin{gather*} \frac {\partial ^2}{\partial x^2} \int _0^{2\pi } F(\psi ,x,y)\,d\psi = \int _0^{2\pi } \frac {\partial ^2}{\partial x^2} F(\psi ,x,y)\,d\psi ,\\ \frac {\partial ^2}{\partial y^2} \int _0^{2\pi } F(\psi ,x,y)\,d\psi = \int _0^{2\pi } \frac {\partial ^2}{\partial y^2} F(\psi ,x,y)\,d\psi \end{gather*}and so
\begin{equation*}\Delta u(x+iy)= \int _0^{2\pi } \frac {\partial ^2}{\partial x^2} F(\psi ,x,y)+ \frac {\partial ^2}{\partial y^2} F(\psi ,x,y)\,d\psi .\end{equation*}But \(F(\psi ,x,y)=f(e^{i\psi }) P(x+iy,e^{i\psi })\) and so
\begin{equation*}\frac {\partial ^2}{\partial x^2} F(\psi ,x,y)+ \frac {\partial ^2}{\partial y^2} F(\psi ,x,y) = f(e^{i\psi }) \Delta P(x+iy,e^{i\psi })=0\end{equation*}and so \(\Delta u(x+iy)=0\), as desired.
Let \(P_r(\theta )=\frac {1}{2\pi }\frac {1-r^2}{{1-2r\cos (\theta )+r^2}}\).
Conclude that if \(v\) is continuous on \(\overline \D \) and harmonic in \(\D \), then
for all \(0\leq r<1\) and all \(\theta \in \R \).
Observe that \(P(re^{i\theta },e^{i\psi } =\frac {|e^{i\psi }|^2-|re^{i\theta }|^2}{|e^{i\psi }-re^{i\theta }|^2}\). Now, First observe that \(|re^{i\theta }|=r\). Next, observe that\begin{align*} |e^{i\psi }-re^{i\theta }|^2 &=(e^{i\psi }-re^{i\theta })(e^{-i\psi }-re^{-i\theta }) \\&=1-re^{i(\theta -\psi )}-re^{i(\psi -\theta )}+r^2 \\&=1-2r\cos (\psi -\theta )+r^2 \end{align*}where we have used the variant \(2\cos \eta =e^{i\eta }+e^{-i\eta }\) of Euler’s identity \(e^{i\eta }=\cos \eta +i\sin \eta \). Thus
\[P(re^{i\theta },e^{i\psi }) =\frac {1-r^2}{1-2r\cos (\psi -\theta )+r^2}.\]Now, observe that if \(0\leq r<1\) then \(1-r^2>0\) and
\[1-2r\cos (\theta )+r^2\geq 1-2r+r^2=(1-r)^2>0\]and so \(P_r(\theta )\) is a positive real number, as desired.
Prove that if \(0\leq r<1\) then \(\int _0^{2\pi } P_r(\theta )\,d\theta =1\).
The function \(v(z)=1\) for all \(z\) is harmonic in \(\C \). Therefore, by Theorem 7.3.3 and 4170Problem 4170 we have that\begin{equation*}1=v(r)=\int _0^{2\pi } v(e^{i\theta }) \,P_r(\theta -0)\,d\theta =\int _0^{2\pi } \,P_r(\theta )\,d\theta \end{equation*}for all \(0\leq r<1\) and all \(\theta \in \R \).
Prove that \(\lim _{r\to 1^-} P_r(\theta )=0\) for all \(\theta \neq 2n\pi \).
If \(\theta \neq 0\) then \(-1\leq \cos \theta <1\). Thus \(1-2(1)\cos \theta +1^2>0\) and so the rational function \(f(r)=P_r(\theta )=\frac {1-r^2}{2\pi (1-2r\cos \theta +r^2)}\) is continuous at \(r=1\). Thus \(\lim _{r\to 1^-} P_r(\theta )=P_1(\theta )=0\).
Let \(0<\delta <\pi \) be a small positive number. Prove that
Because \(\cos \) is monontonically decreasing on \([0,\pi ]\), and because \(\cos (2\pi -\theta )=\cos \theta \), we have that if \(\delta <\theta <2\pi -\delta \) then \(\cos \theta <\cos \delta <1\). Thus \(\sup _{\delta <\theta <2\pi -\delta } P_r(\theta )\leq P_r(\delta )\). Recall \(P_r(\theta )>0\) for all \(\theta \in \R \) and all \(0\leq r<1\).Because \(\lim _{r\to 1^-} P_r(\delta )=0\), we have that \(\lim _{r\to 1^-} \sup _{\delta <\theta <2\pi -\delta } |P_r(\theta )|=0\) and so we must have that \(P_r\to 0\) as \(r\to 1^-\) uniformly for \(\theta \in (\delta ,2\pi -\delta )\).
Let \(u\), \(f\) be as in Theorem 7.3.4. Show that \(u(re^{i\theta })\) converges to \(f(e^{i\theta })\) as \(r\to 1^-\) uniformly in \(\theta \).
We compute that\begin{align*} u(re^{i\theta })-f(e^{i\theta }) &= \int _0^{2\pi } f(e^{i\psi }) P_r(\psi -\theta )\,d\psi -f(e^{i\theta }) \end{align*}by 4170Problem 4170 and the \(2\pi \)-periodicity of \(P_r\).
By 4180Problem 4180, we have that
\[f(e^{i\theta })=\int _0^{2\pi } f(e^{i\theta })P_r(\psi -\theta )\,d\psi \]and so
\begin{align*} u(re^{i\theta })-f(e^{i\theta }) &= \int _0^{2\pi } \bigl (f(e^{i\psi })-f(e^{i\theta })\bigr ) P_r(\psi -\theta )\,d\psi .\end{align*}Thus because \(P_r>0\) we have that
\begin{align*} |u(re^{i\theta })-f(e^{i\theta })| &\leq \int _0^{2\pi } \bigl |f(e^{i\psi })-f(e^{i\theta })\bigr | P_r(\theta -\psi )\,d\psi .\end{align*}Because \(\partial \D \) is compact and \(f\) is continuous on \(\partial \D \), we have that \(f\) is bounded and uniformly continuous. Choose some \(\varepsilon >0\). There is a \(\delta >0\) such that if \(|\theta -\psi |<\delta \) then \(|f(\theta )-f(\psi )|<\varepsilon \).
By the \(2\pi \)-periodicity of \(P_r\), we have that
\begin{align*} \int _0^{2\pi } &\bigl |f(e^{i\psi })-f(e^{i\theta })\bigr | P_r(\theta -\psi )\,d\psi \\&= \int _{\theta -\delta }^{\theta +\delta } \bigl |f(e^{i\psi })-f(e^{i\theta })\bigr | P_r(\theta -\psi )\,d\psi + \int _{\theta +\delta }^{\theta +2\pi -\delta } \bigl |f(e^{i\psi })-f(e^{i\theta })\bigr | P_r(\theta -\psi )\,d\psi .\end{align*}By definition of \(\delta \) and nonnegativity of \(P_r\) we have that
\begin{align*} \int _0^{2\pi } &\bigl |f(e^{i\psi })-f(e^{i\theta })\bigr | P_r(\theta -\psi )\,d\psi \\&\leq \varepsilon \int _{\theta -\delta }^{\theta +\delta } P_r(\theta -\psi )\,d\psi + 2\max _{\partial \D } |f| \int _{\theta +\delta }^{\theta +2\pi -\delta } P_r(\theta -\psi )\,d\psi .\end{align*}Invoking nonnegativity of \(P_r\) in the first integral and the \(2\pi \)-periodicity of \(P_r\) in both integrals yields that
\begin{align*} \int _0^{2\pi } &\bigl |f(e^{i\psi })-f(e^{i\theta })\bigr | P_r(\theta -\psi )\,d\psi \\&\leq \varepsilon \int _{0}^{2\pi } P_r(\psi )\,d\psi + 2\max _{\partial \D } |f| \int _{\delta }^{2\pi -\delta } P_r(\psi )\,d\psi .\end{align*}The first integral is \(1\) by 4180Problem 4180, while the second integrand converges uniformly to \(0\) as \(r\to 1^-\). Thus there is a \(\varrho <1\) depending on \(\varepsilon \) (but not on \(\theta \)) such that if \(\varrho <r<1\), then
\begin{align*} \int _0^{2\pi } \bigl |f(e^{i\psi })-f(e^{i\theta })\bigr | P_r(\theta -\psi )\,d\psi &\leq \varepsilon + 2\max _{\partial \D } |f| \varepsilon .\end{align*}Combining with our above estimate for \(|u(re^{i\theta })-f(e^{i\theta })|\) completes the proof.
Let \(u\), \(f\) be as in Theorem 7.3.4. Show that \(u\) is continuous on \(\overline \D \). (This completes the proof of Theorem 7.3.4. This differs from the previous problem in that the previous problem considers \(u(z)\) as \(z\to e^{i\theta }\) along a ray through the origin, while this problem considers \(u(z)\) as \(z\to e^{i\theta }\) along arbitrary paths.)
Write an analogue to Theorem 7.3.4 in an arbitrary disc. That is, let \(P\in \C \), \(r>0\), and \(f:\partial D(P,r)\to \R \) be continuous. Show that there is a function \(u\) that is harmonic in \(D(P,r)\), continuous on \(\overline D(P,r)\), and satisfies \(u(z)=f(z)\) for all \(z\in \partial D(P,r)\). Can you write a formula for \(u\) in \(D(P,r)\)?
If \(z\in \D \), define\begin{equation*}v(z)=\frac {1}{2\pi }\int _0^{2\pi } f(P+re^{i\theta }) \frac {1-|z|^2}{|e^{i\theta }-z|^2}\,d\theta .\end{equation*}By Theorem 7.3.4 we have that \(v\) is continuous on \(\overline D\), harmonic in \(\D \) and satisfies \(v(e^{i\theta })=f(P+re^{i\theta })\).
If we let \(u(z)=v(\frac {1}{r}(z-P))\), a straightforward computation shows that \(u\) is harmonic in \(D(P,r)=\{z\in \C :\frac {1}{r}(z-P)\in \D \}\), continuous on \(\overline D(P,r)\), and satisfies \(u(P+re^{i\theta })=v(e^{i\theta })=f(P+re^{i\theta })\), that is, \(u=f\) on \(\partial D(P,r)\). We compute that
\begin{equation*}u(z)=v\biggl (\frac {1}{r}(z-P)\biggr ) =\frac {1}{2\pi }\int _0^{2\pi } f(P+re^{i\theta }) \frac {1-|(z-P)/r|^2}{|e^{i\theta }-(z-P)/r|^2}\,d\theta \end{equation*}which simplifies to
\begin{equation*}u(z) =\frac {1}{2\pi }\int _0^{2\pi } f(P+re^{i\theta }) \frac {r^2-|z-P|^2}{|P+re^{i\theta }-z|^2}\,d\theta .\end{equation*}
If \(u\) is harmonic in \(\H =\{x+iy:x\in \R ,\>y>0\}\) and continuous on \(\overline \H \), and if \(\lim _{|z|\to \infty } u(z)\) exists (and is finite), then
for all \(x\in \R \) and all \(y\in (0,\infty )\).
Conversely, if \(f:\R \to \R \) is continuous, if \(\lim _{t\to \infty } f(t)=\lim _{t\to -\infty } f(t)\in \R \), and if we define
then \(u\) is harmonic in \(\H \) and continuous on \(\overline \H \).
Suppose that \(f:\R \to \R \) is bounded and continuous. However, we do not require that \(\lim _{t\to \infty } f(t)\) or \(\lim _{t\to -\infty } f(t)\) exist. Show that if
then we still have that \(u\) is harmonic in \(\H =\{x+iy:x\in \R ,\>y>0\}\) and continuous on \(\overline \H \).
Suppose that \(u\) and \(v\) are harmonic in some open set \(\Omega \), that \(\overline D(P,r)\subset \Omega \), and that \(u(z)=v(z)\) for all \(z\in \partial D(P,r)\). Show that \(u(z)=v(z)\) for all \(z\in D(P,r)\).
If \(u\) is harmonic in a connected open set \(\Omega \) and \(u=0\) in \(D(P,r)\) for some \(D(P,r)\subseteq \Omega \) with \(r>0\), then \(u=0\) everywhere in \(\Omega \).
Give an example of two harmonic functions that are equal on a set with an accumulation point but are not equal everywhere.
Show that the zeroes of a real harmonic function cannot be isolated. That is, let \(\Omega \subseteq \C \) be open and let \(u:\Omega \to \R \) be harmonic. Let \(P\in \Omega \) with \(u(P)=0\) and let \(r>0\). Show that \(u(z)=0\) for some \(z\in D(P,r)\setminus \{P\}\).
Let \(a<b\) and let \(f:[a,b]\to \R \) be a nonnegative continuous function that satisfies \(\int _a^b f=0\). Show that \(f(x)=0\) for all \(x\in [a,b]\).
Let \(\Omega \subset \C \) be open and let \(h:\Omega \to \R \) be continuous. We say that \(h\) has the small circle mean value property (SCMV property) if, for every \(P\in \Omega \), there is some number \(\varepsilon _P>0\) such that \(D(P,\varepsilon _P)\subset \Omega \) and such that \(h(P)=\frac {1}{2\pi }\int _0^{2\pi } h(P+\varepsilon e^{i\theta })\,d\theta \) for all \(0<\varepsilon <\varepsilon _P\).
If \(u\) is harmonic in an open set \(\Omega \), then \(u\) has the small circle mean value property, and if \(P\in \Omega \) then \(\varepsilon _P\) is the largest number such that \(D(P,\varepsilon _P)\subseteq \Omega \).
Let \(\Omega \subset \C \) be open and connected. Let \(g\) be continuous on \(\Omega \) and satisfy the “small circle” mean value property. Suppose furthermore that there is some \(P\in \Omega \) such that \(g(P)\geq g(z)\) for all \(z\in \Omega \). Then \(g\) is constant.
Prove Lemma 7.4.4.
Let \(E=\{z\in \Omega :g(z)=g(P)\}=g^{-1}(\{g(P)\})\). Then \(E\) is relatively closed in \(\Omega \) because \(g\) is continuous.Let \(z\in E\). We then know that
\begin{equation*}g(P)=g(z)=\frac {1}{2\pi } \int _0^{2\pi } g(z+re^{i\theta })\,d\theta \end{equation*}for all \(0<r<\varepsilon _z\). Rewriting, we have that
\begin{equation*}0=\int _0^{2\pi } g(P)-g(z+re^{i\theta })\,d\theta \end{equation*}for all \(0<r<\varepsilon _z\).
Observe that \(f(\theta )=g(P)-g(z+re^{i\theta })\) is continuous and nonnegative because \(g(P)\geq g(w)\) for all \(w\in \Omega \). Thus by 4270Problem 4270, we have that \(f(\theta )=0\) for all \(\theta \in [0,2\pi ]\) and so \(g(z+re^{i\theta })=g(P)\) for all \(0<r<\varepsilon _z\) and all \(\theta \in \R \). By assumption \(g(z)=g(P)\), so we have that \(D(z,\varepsilon _z)\subseteq E\). Thus \(E\) is open. Because \(E\subseteq \Omega \) is nonempty, open, and (relatively) closed, and \(\Omega \) is connected, we have that \(E=\Omega \) and so \(u(z)=u(P)\) for all \(z\in \Omega \).
Suppose that \(g\) is continuous on \(\overline D(P,r)\) and has the “small circle” mean value property in \(D(P,r)\). Suppose further that \(g=0\) on \(\partial D(P,r)\). Show that \(g=0\) in \(D(P,r)\).
Because \(\overline D(P,r)\) is compact and \(g\) is continuous, there are points \(\zeta \), \(\omega \in \overline D(P,r)\) such that \(g(\zeta )\geq g(z)\geq g(\omega )\) for all \(z\in \overline D(P,r)\).If \(\zeta \in D(P,r)\) then \(g\) is constant by Lemma 7.4.4. Because \(g(z)=0\) for some \(z\in \overline D(P,r)\) (in fact all \(z\in \partial D(P,r)\)), if \(g\) is constant then \(g\equiv 0\).
If \(\omega \in D(P,r)\), observe that \(h=-g\) is also continuous and has the SCMVP; thus, by Lemma 7.4.4, \(h\) and thus \(g\) is constant. Again if \(g\) is constant then \(g\equiv 0\).
Finally, if \(\zeta \), \(\omega \in \partial D(P,r)\) then
\begin{equation*}0=g(\omega )\leq g(z)\leq g(\zeta )=0\end{equation*}for all \(z\in \overline D(P,r)\), and so \(g\equiv 0\).
Suppose that \(g\) and \(h\) are continuous on \(\overline D(P,r)\) and that \(g=h\) on \(\partial D(P,r)\). Suppose that \(h\) is harmonic in \(D(P,r)\) and that \(g\) has the “small circle” mean value property in \(D(P,r)\). Show that \(g=h\) in \(D(P,r)\) as well.
Let \(f=g-h\). Then \(f\) is clearly continuous on \(\overline D(P,r)\). Because \(h\) is harmonic, by Theorem 7.2.5 it has the mean value property in \(D(P,r)\). Thus, if \(z\in D(P,r)\) and \(\varepsilon _z\) is as in the definition of SCMVP for \(g\), we have that\begin{align*} f(z) &=g(z)-h(z) =\frac {1}{2\pi }\int _0^{2\pi } g(z+\rho e^{i\theta })\,d\theta -\frac {1}{2\pi }\int _0^{2\pi } h(z+\rho e^{i\theta })\,d\theta =\frac {1}{2\pi }\int _0^{2\pi } f(z+\rho e^{i\theta })\,d\theta \end{align*}for all \(0<\rho <\varepsilon _z\). Thus \(f\) has the SCMVP in \(D(P,r)\). Furthermore, \(f=0\) on \(\partial D(P,r)\), and so by the previous problem, \(f=0\) in \(D(P,r)\) as well.
Let \(\Omega \subseteq \C \) be open. Suppose that \(g:\Omega \to \R \) is continuous and has the “small circle” mean value property in \(\Omega \). Then \(g\) is harmonic in \(\Omega \).
Prove Theorem 7.4.2.
Let \(P\in \Omega \). Then there is a \(r>0\) such that \(\overline D(P,r)\subset \Omega \). Observe that \(g\) is continuous on \(\partial D(P,r)\). By Theorem 7.3.4 (or rather, by 4230Problem 4230) there is a function \(u:\overline D(P,r)\to \R \) that is continuous on \(\overline D(P,r)\), harmonic in \(D(P,r)\), and satisfies \(u=g\) on \(\partial D(P,r)\). By 4300Problem 4300, we have that \(g=u\) in \(D(P,r)\) and so \(g\) must be harmonic in \(D(P,r)\) as well. This is true for every \(P\in \Omega \), so \(g\) must be harmonic in all of \(\Omega \).
Let \(\Omega \subset \C \) be open. Suppose that \(\{h_j\}_{j=1}^\infty \) is a sequence of functions, each harmonic on \(\Omega \), and that \(h_j\to h\) uniformly on compact subsets of \(\Omega \). Then \(h\) is also harmonic.
Prove Corollary 7.4.3. Hint: Show that \(h\) has the “small circle” mean value property.
Let \(P\in \Omega \) and let \(r>0\) be such that \(\overline D(P,r)\subset \Omega \). It is a standard result in undergraduate analysis that the uniform limit of a sequence of continuous functions is continuous, and so \(h\) is continuous in \(\Omega \).
Then
\begin{align*} h(P)&=\lim _{j\to \infty } h_j(P) = \lim _{j\to \infty } \frac {1}{2\pi } \int _0^{2\pi } h_j(P+re^{i\theta })\,d\theta \end{align*}by Theorem 7.2.5. But \(h_j\to h\) uniformly on the compact set \(\partial D(P,r)\), and so by 750Memory 750
\begin{align*} h(P)&=\frac {1}{2\pi } \int _0^{2\pi } \lim _{j\to \infty } h_j(P+re^{i\theta })\,d\theta \\&=\frac {1}{2\pi } \int _0^{2\pi } h(P+re^{i\theta })\,d\theta . \end{align*}The right hand side must exist because \(h\) is continuous and thus integrable. Thus \(h\) has the small circle mean value property in \(\Omega \), and so is harmonic by Theorem 7.4.2.
Let \((X,d)\) and \((Z,\varrho )\) be two metric spaces. Let \(D\), \(F\subseteq X\) and suppose that \(D\) and \(F\) are both (relatively) closed in \(\Psi =D\cup F\). Suppose that \(h:D\cup F\to Z\). If \(h\big \vert _D\) and \(h\big \vert _F\) are both continuous, show that \(h\) is continuous on all of \(\Psi \).
If \(C\subseteq Z\) is closed, then because \(v=h\big \vert _D\) and \(w=h\big \vert _F\) are continuous we must have that \(v^{-1}(C)\) and \(w^{-1}(C)\) are relatively closed in \(D\) and \(F\), respectively. Because \(D\) and \(F\) are (relatively) closed in \(\Psi \) we have that \(v^{-1}(C)\) and \(w^{-1}(C)\) are relatively closed in \(\Psi \). Thus their union is relatively closed. But \(h^{-1}(C)=v^{-1}(C)\cup w^{-1}(C)\), and so \(h^{-1}(C)\) is relatively closed in \(\Psi \). Recalling that this is equivalent to continuity completes the proof.
Let \(\Psi \subset \C \) be open and connected. Suppose that \(\Psi \) is symmetric about the real axis; that is, \(z\in \Psi \) if and only if \(\bar z\in \Psi \). Let \(\Omega =\{z\in \Psi :\im z>0\}\).
Let \(v:\Omega \to \R \) be harmonic. Suppose that
for all \(x\in \Psi \cap \R \).
Then there is a function \(\widehat v:\Psi \to \R \) that is harmonic in \(\Psi \) and satisfies \(\widehat v=v\) in \(\Omega \). Furthermore,
Let \(\Psi \), \(\Omega \), and \(v\) be as in Lemma 7.5.1.
Sketch \(\Psi \). Label \(\Omega \), \(\widehat \Omega \), the set where \(v\) is harmonic, and the set where \(v\) is equal to zero.
Show that \(\R \cap \Psi =\partial \Omega \cap \Psi \). Give an example to show that \(\R \cap \partial \Omega \) may not equal \(\R \cap \Psi \).
Suppose that \(\Omega \subseteq \H \), that \(\widehat \Omega =\{z\in \C :\bar z\in \Omega \), and that \(F\subseteq \R \). Suppose \(\Psi =\Omega \cap F\cap \widehat \Omega \). What must be true about \(F\) and \(\Omega \) in order for \(\Psi \) and \(\Omega \) to satisfy the conditions of Lemma 7.5.1?
We need only check that \(\Psi \) is open. Thus, we need only check that if \(z\in F\) then \(D(z,r)\subseteq \Psi \) for some \(r>0\).Thus, \(\Psi \) satisfies the conditions of Lemma 7.5.1 if and only if \(F\subset \R \) is open as a set of real numbers (not as a set of complex numbers), and if \(z\in F\) then there is a \(r>0\) such that if \(\H \cap D(z,r)\subseteq \Omega \). (A necessary, but not sufficient, condition for the second requirement is that \(F\subseteq \partial \Omega \).)
Suppose \(\Omega \subset \C \) is open and that \(v\) is harmonic on \(\Omega \). Let \(w(z)={v(\bar z)}\). Show that \(w\) is harmonic on \(\widehat \Omega =\{z\in \C :\bar z\in \Omega \}\).
This is an easy consequence of Problem 1.34 and 4020Problem 4020.
Let \(\Psi \), \(\Omega \), \(\widehat \Omega \), \(v\), and \(\widehat v\) be as in Lemma 7.5.1. Show that \(\widehat v\) is continuous in \(\Psi \).
Let \(\Phi =\overline \Omega \cap \Psi \) and let \(\widehat \Phi =\{z\in \Psi :\bar z\in \Phi \}\). Then \(\Phi \) and \(\widehat \Phi \) are relatively closed in \(\Psi \).If \(z\in \Omega \) then \(\widehat v\) is continuous at \(z\) because \(\widehat v=v\) in a neighborhood of \(v\),
If \(x\in \R \cap \Psi \), then \(\lim _{\substack {z\to x\\z\in \Phi }}\widehat v(z)=0=\widehat v(x)\), and so \(\widehat v\) is continuous on \(\Phi \).
Observe that \(\widehat v(w)=-v(\overline w)\) for all \(w\in \Psi \), and so because \(\widehat v\) is continuous on \(\Phi \) we have that it is continuous on \(\widehat \Phi \).
The result follows from 4340Problem 4340.
Suppose that \(v\), \(\widehat v\), and \(\Psi \) are as in Lemma 7.5.1. Show that \(\widehat v\) is harmonic in \(\Psi \). This completes the proof of Lemma 7.5.1.
Let \(z\in \Psi \). Then either \(z\in \Omega \), \(z\in \widehat \Omega \), or \(z\in \R \cap \Psi \).If \(z\in \Omega \) or \(z\in \widehat \Omega \), let \(r>0\) be such that \(D(z,r)\subseteq \Omega \) or \(D(z,r)\subseteq \widehat \Omega \). By assumption, or by 4360Problem 4360, \(\widehat v\) is harmonic in \(\Omega \) and in \(\widehat \Omega \), and thus in either case is harmonic in \(D(P,r)\). By Theorem 7.2.5, we have that for every \(\rho \) with \(0<\rho <r\), it holds that \(\widehat v(z)=\frac {1}{2\pi } \int _0^{2\pi } \widehat v(z+\rho e^{i\theta })\,d\theta \).
Now consider the case where \(z\in \R \). By assumption \(\Psi \) is open and so there is a \(r>0\) such that \(D(z,r)\subseteq \Psi \). Let \(0<\rho <r\). Because \(\widehat v\) is continuous on \(\Psi \), it is integrable, and so
\begin{align*} \frac {1}{2\pi } \int _0^{2\pi } \widehat v(z+\rho e^{i\theta })\,d\theta &=\frac {1}{2\pi } \int _0^{\pi } \widehat v(z+\rho e^{i\theta })\,d\theta + \frac {1}{2\pi } \int _\pi ^{2\pi } \widehat v(z+\rho e^{i\theta })\,d\theta \\&=\frac {1}{2\pi } \int _0^{\pi } v(z+\rho e^{i\theta })\,d\theta + \frac {1}{2\pi } \int _\pi ^{2\pi } - v(z+\rho e^{-i\theta })\,d\theta . \end{align*}Making the change of variables \(\psi =2\pi -\theta \) in the second integral, we have that
\begin{align*}\frac {1}{2\pi } \int _0^{2\pi } \widehat v(z+\rho e^{i\theta })\,d\theta &=\frac {1}{2\pi } \int _0^{\pi } v(z+\rho e^{i\theta })\,d\theta - \frac {1}{2\pi } \int _0^{\pi } v(z+\rho e^{-i(2\pi -\psi )})\,d\psi \\&=\frac {1}{2\pi } \int _0^{\pi } v(z+\rho e^{i\theta })\,d\theta - \frac {1}{2\pi } \int _0^{\pi } v(z+\rho e^{i\psi })\,d\psi =0=\widehat v(z). \end{align*}Thus \(v\) satisfies the SCMVP in \(\Psi \), and so must be harmonic by Theorem 7.4.2. This completes the proof of Lemma 7.5.1.
Let \(\Psi \) and \(\Omega \) be as in Lemma 7.5.1. That is, let \(\Psi \subset \C \) be open, connected, and symmetric about the real axis. Let \(\Omega =\{z\in \Psi :\im z>0\}\).
Let \(f:\Omega \cap \Psi \to \R \) be holomorphic. Suppose that \(f\) is holomorphic in \(\Omega \) and that
for all \(x\in \Psi \cap \R \).
Then there is a function \(\widehat f:\Psi \to \R \) that is holomorphic in \(\Psi \) and satisfies \(\widehat f=f\) in \(\Omega \), \(\im \widehat f(z)=0\) on \(\Psi \cap \R \), and \(\widehat f(z)=\overline { f(\bar z)}\) in \(\widehat \Omega \).
Suppose \(\Omega \subset \C \) is open and that \(f\) is holomorphic on \(\Omega \). Let \(g(z)=\overline {f(\bar z)}\). Then \(g\) is holomorphic on \(\widehat \Omega =\{z\in \C :\bar z\in \Omega \}\).
Suppose that \(f\) is holomorphic in \(D(x_0,r)\) for some \(x_0\in \R \) and some \(r>0\). Suppose further that \(f(x)\) is real for all \(x\in (x_0-r,x_0+r)=D(x_0,r)\cap \R \). Show that \(f(z)=\overline {f(\bar z)}\) for all \(z\in D(x_0,r)\).
By the previous problem, \(g(z)=f(z)-\overline {f(\bar z)}\) is holomorphic in \(D(x_0,r)\). Because \(f(x)\) is real for all \(x\in \R \cap D(x_0,r)\), we have that \(g(x)=0\) on \(\R \cap D(x_0,r)\), a set with an accumulation point. Thus \(g\equiv 0\) in \(D(x_0,r)\) and so \(f(z)=\overline { f(\bar z)}\).
Prove Theorem 7.5.2. Hint: Start by considering discs in \(\Psi \) centered at a point on the real axis.
Define \(\widehat f\) on \(\Omega \cap \widehat \Omega \) as in the theorem statement. We wish to show that \(\lim _{\substack {z\to x\\z\in \Omega }}f(z)\) exists for each \(x\in \R \cap \Psi \). Because \(\lim _{\substack {z\to x\\z\in \Omega }}\im f(z)=0\), as in the proof of 4370Problem 4370 this will imply that \(\widehat f\) may be extended to a function continuous on \(\Psi \). We wish also to show that the extension \(\widehat f\) is also holomorphic in a neigborhood of each \(x_0\in \R \cap \Psi \).Let \(f=u+iv\) where \(u\) and \(v\) are real functions; they are then harmonic in \(\Omega =\{z\in \Psi :\im z>0\} \) and \(\lim _{\substack {z\to x\\z\in \Omega }}v(z)=0\) for all \(x\in \R \cap \Psi \). By Lemma 7.5.1, we have that there is a function \(\widehat v\) harmonic in \(\Psi \) that equals \(v\) in \(\Omega \) (and in fact \(\widehat v=\im \widehat f\) everywhere \(\widehat f\) has thus far been defined).
If \(x_0\in \R \cap \Psi \), there is a \(r>0\) with \(D(x_0,r)\subseteq \Psi \). Then there is a holomorphic function \(g:D(x_0,r)\to \C \) with \(\im g=\widehat v\) in \(D(x_0,r)\). Then \(\widehat f-g\) is holomorphic in \(\{z\in D(x_0,r):\im z>0\}\) and also in \(\{z\in D(x_0,r):\im z<0\}\); because \(\im \widehat f=\widehat v=\im g\), we have that \(\widehat f-g\) is purely real and so must be constant in each of those two connected open sets.
But \(g\) is continuous on all of \(D(x_0,r)\), and as noted above if \(\lim _{\substack {z\to x\\z\in \Omega }}f(z)\) exists then it must equal \(\lim _{\substack {z\to x\\z\in \widehat \Omega }}f(z)\). Thus we must have that \(\widehat f-g\) is equal to one constant in all of \(D(x_0,r)\); thus \(\widehat f\) extends by continuity to a function holomorphic in all of \(D(x_0,r)\), as desired.
Suppose that \(f\) is holomorphic on \(\H =\{z\in \C :\im z>0\}\) and that \(\lim _{\substack {z\to x\\z\in \Omega }}f(z)=0\) for all \(0<x<1\). Show that \(f(z)=0\) for all \(z\in \H \).
Let \(\Psi =D(1/2,1/2)\), \(\Omega =\H \cap \Psi \). Then by Theorem 7.5.2 there is a function \(\widehat f\) holomorphic in \(\Psi \) and with \(\widehat f=f\) in \(\Omega \).But the zeroes of \(\widehat f\) have an accumulation point in \(\Psi \), and so \(\widehat f\equiv 0\) in \(\Psi \). Thus \(f\equiv 0\) in \(\Omega \subset \H \), and because \(\Omega \) has an accumulation point in \(\H \) we again have that \(f\equiv 0\) in \(\H \).
Let \(\{x_j\}_{j=1}^\infty \) be an increasing sequence of real numbers, that is, \(x_j\in \R \) and \(x_j\leq x_{j+1}\) for all \(j\in \N \). Then either \(x_j\to \infty \) or \(x_j\to x\) for some \(x\in \R \).
If \(E\) is a set, \((X,d)\) is a complete metric space, \(f_k:E\to X\), and \(\{f_k\}_{k=1}^\infty \) is uniformly Cauchy, then \(\{f_k\}_{k=1}^\infty \) converges uniformly to some \(f:E\to X\).
Recall that if \(u\) is harmonic in \(D(P,R)\) and continuous on \(\overline D(P,R)\), then for any \(0\leq r<R\) and any \(0\leq \theta \leq 2\pi \),
Show that
and
First, if \(R\), \(r\), \(\theta \), and \(\psi \) are real, then\begin{align*} |Re^{i\psi }-re^{i\theta }| &=|Re^{i(\psi -\theta )} -r| \\&= \sqrt {(R\cos (\psi -\theta )-r)^2+R^2\sin ^2(\psi -\theta )} \\&= \sqrt {R^2 + r^2 -2Rr\cos (\psi -\theta )} \end{align*}which clearly has a minimum value of \(\sqrt {R^2+r^2-2Rr}=R-r\) (attained if \(\theta =\psi \)) and a maximum value of \(\sqrt {R^2+r^2+2Rr}=R+r\). (This is attained if \(\psi =\theta \pm \pi \); if \(0\leq \theta \leq 2\pi \) then either \(\theta \leq \pi \) and so \(\psi =\theta +\pi \in [0,2\pi ]\) or \(\theta \geq \pi \) and so \(\psi =\theta -\pi \in [0,2\pi ]\). In either case the maximum value \(R+r\) is attained for some \(\psi \) in the given range.)
Thus,
\begin{equation*}\frac {R-r}{R+r}=\frac {R^2-r^2}{(R+r)^2} \leq \frac {R^2-r^2}{|Re^{i(\psi -\theta )}-r|^2} \leq \frac {R^2-r^2}{(R-r)^2}=\frac {R+r}{R-r}\end{equation*}and the left-hand and right-hand bound, respectively, is attained at \(\theta =\psi \pm \pi \) and \(\theta =\psi \).
(The Harnack inequality.) Suppose that \(u\) is nonnegative and harmonic in \( D(P,R)\) and continuous on \(\overline D(P,R)\). If \(z\in D(P,R)\) with \(r=|z-P|\), then
Prove Corollary 7.6.2.
Fix some such \(z\) and let \(r\), \(\theta \) be real numbers with \(r\geq 0\) and such that \(z=P+re^{i\theta }\). Then \(r=|z-P|\). Because \(u(P+Re^{i\psi })\geq 0\) for all \(\psi \), we have that by the previous problem,\begin{align*} \frac {R-r}{R+r} u(P+Re^{i\psi }) &\leq u(P+Re^{i\psi })\frac {R^2-r^2}{|Re^{i\psi }-re^{i\theta }|} \leq u(P+Re^{i\psi })\frac {R+r}{R-r}.\end{align*}Therefore,
\begin{multline*} \int _0^{2\pi }\frac {R-r}{R+r} u(P+Re^{i\psi }) \,d\psi \\\leq \int _0^{2\pi } u(P+Re^{i\psi })\frac {R^2-r^2}{|Re^{i\psi }-re^{i\theta }|}\,d\psi \\\leq \int _0^{2\pi } u(P+Re^{i\psi })\frac {R+r}{R-r}\,d\psi .\end{multline*}Because \(\frac {R-r}{R+r}\) and \(\frac {R+r}{R-r}\) are independent of \(\psi \) we may move them out of the integral. Then we may use the mean value property on the outer integrals and the Poisson integral formula on the inner integral to see that
\begin{equation*}\frac {R-r}{R+r} u(P)\leq u(z)\leq \frac {R+r}{R-r}u(P)\end{equation*}as desired.
Did we need the assumption that \(u\) was continuous on \(\overline D(P,R)\)?
No. If \(u\) is nonnegative and harmonic in \(D(P,R)\), then \(u\) is nonnegative and harmonic in \(D(P,\rho )\) and continuous on \(\overline D(P,\rho )\) for all \(0<\rho <R\). We then have that\begin{equation*}\frac {\rho -r}{\rho +r} u(P)\leq u(z)\leq \frac {\rho +r}{\rho -r}u(P)\end{equation*}for all \(\rho \) with \(r<\rho <R\), and taking the limit as \(\rho \to R^-\) completes the proof.
(Harnack’s principle.) Let \(\{u_k\}_{k=1}^\infty \) be a sequence of real-valued functions harmonic in a connected open set \(\Omega \subseteq \C \) such that \(u_1(z)\leq u_2(z)\leq u_3(z)\leq \cdots \) for each \(z\in \Omega \). Then either \(u_k\to \infty \) uniformly on compact sets or there is a function \(u:\Omega \to \R \) such that \(u_k\to u\) uniformly on compact sets.
(By Corollary 7.4.3, \(u\) is harmonic.)
In this problem we begin the proof of Theorem 7.6.3. Let \(\Omega \) and \(u_k\) be as in Theorem 7.6.3. Let \(P\in \Omega \). Suppose that \(\smash {\lim _{k\to \infty } u_k(P)=\infty }\). Show that there is a \(r>0\) such that \(\overline D(P,r)\subset \Omega \) and such that \(u_k\to \infty \) uniformly on \(\overline D(P,r)\).
Let \(R>0\) be such that \(D(P,R)\subseteq \Omega \). Define \(v_k=u_k-u_1\). Then \(v_k:\Omega \to \R \) is harmonic, and \(v_k\geq 0\).Fix some \(r\in (0,R)\). Let \(M\in \R \). By definition of \(u_k(P)\to \infty \), there is some \(K\in \N \) such that, if \(k\geq K\), then \(u_k(P)\geq M\).
We have that each \(v_k\) is harmonic and nonnegative in \(D(P,R)\). Then, if \(z\in \overline D(P,r)\), then by Harnack’s inequality, if \(k\geq K\) then
\begin{align*} u_k(z)&=v_k(z)+u_1(z) \geq \frac {R-|z-P|}{R+|z-P|}v_k(P)+u_1(z) \\&\geq M\frac {R-r}{R+r} + \min _{\overline D(P,r)} u_1 \geq M\frac {R-r}{R+r} - \max _{\overline D(P,r)} |u_1| \end{align*}where the final term is finite because \(u_1\) is continuous and \(\overline D(P,r)\) is compact, and where we have used that if \(|z-P|\leq r<R\) then \(\frac {R-|z-P|}{R+|z-P|}\leq \frac {R-r}{R+r}\). Thus \(u_k\to \infty \) uniformly on \(\overline D(P,r)\).
Suppose that \(\lim _{k\to \infty } u_k(P)<\infty \). Show that there is a \(r>0\) such that \(\overline D(P,r)\subset \Omega \) and such that \(\{u_k\}_{k=1}^\infty \) converges uniformly on \(\overline D(P,r)\) to a finite function.
Let \(R\) be as in the previous problem and let \(0<r<R\). We claim that \(\{u_k\}_{k=1}^\infty \) is uniformly Cauchy on \(\overline D(P,r)\). (Because \(\C \) is complete, by 1550Memory 1550 this suffices to establish uniform convergence.)Let \(\varepsilon >0\). Then \(\{u_k(P)\}_{k=1}^\infty \) is a convergent sequence of real numbers, and therefore it is a Cauchy sequence of real numbers. Thus there is a \(N\in \N \) such that if \(k\), \(\ell >N\) then \(|u_k(P)-u_\ell (P)|<\varepsilon \).
Now, let \(k\), \(\ell >N\) and let \(z\in \overline D(P,r)\). Without loss of generality we may take \(k<\ell \). Then \(u_k-u_\ell \geq 0\) everywhere in \(D(P,R)\), and so by Harnack’s inequality, if \(z\in \overline D(P,r)\) then
\begin{align*} 0&\leq u_k(z)-u_\ell (z) \leq \frac {R+r}{R-r}(u_k(P)-u_\ell (P)) <\frac {R+r}{R-r}\varepsilon . \end{align*}Thus if \(k\), \(\ell >N\) then \(|u_k(z)-u_\ell (z)|<\frac {R+r}{R-r}\varepsilon \) for all \(z\in \overline D(P,r)\), and so \(\{u_k\}_{k=1}^\infty \) is uniformly Cauchy on \(\overline D(P,r)\), as desired.
Show that either \(\lim _{k\to \infty } u_k(z)=\infty \) for all \(z\in \Omega \) or \(\lim _{k\to \infty } u_k(z)<\infty \) for all \(z\in \Omega \).
Let \(E=\{z\in \Omega :\lim _{k\to \infty }u_k(z)\in \R \}\) and let \(D=\{z\in \Omega :\lim _{k\to \infty } u_k(z)=\infty \}\). If \(z\in \Omega \), then \(\{u_k(z)\}_{k=1}^\infty \) is an increasing sequence of real numbers, and so \(z\) is in exactly one of \(D\) or \(E\); thus \(\Omega =D\cup E\) and \(D\cap E=\emptyset \).By 4460Problem 4460, \(D\) is open. By 4470Problem 4470, \(E\) is open. Thus by definition of connectedness, either \(\Omega =D\) or \(\Omega =E\).
Prove Theorem 7.6.3.
Suppose that \(\lim _{k\to \infty } u_k(z)=\infty \) for all \(z\in \Omega \). Then for all \(P\in \Omega \) there is a \(r_P>0\) such that \(u_k\to \infty \) uniformly on \(D(P,r_P)\).
Let \(K\subset \Omega \) be compact. Then \(\{D(P,r_P):P\in K\}\) is an open cover of \(K\). It thus has a finite subcover \(K\subset \bigcup _{n=1}^N D(P_n,r_n)\) (with \(r_n=r_{P_n}\)). We have that \(u_k\to \infty \) uniformly on \(D(P_n,r_n)\) for all \(1\leq n\leq N\), and thus for all \(L\in \R \) there is a \(M_n\in \N \) such that if \(k\geq M_n\) then \(u_k\geq L\) in \(D(P_n,r_n)\). Letting \(M=\max \{M_1,\dots ,M_n\}\), we see that if \(k\geq M\) then \(u_k\geq L\) in \(\bigcup _{n=1}^N D(P_n,r_n)\supset K\), as desired.
The argument for the finite case is similar.
Suppose that \(u\) and \(v\) are both real-valued and continuous in a set \(\Omega \). Let \(f(z)=\max (u(z),v(z))\). Then \(f\) is continuous in \(\Omega \).
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \R \) be continuous. Suppose that for every \(\overline D(P,r)\subset \Omega \), we have that
Then we say that \(f\) is subharmonic in \(\Omega \).
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \R \) be continuous. Suppose that for every \(\overline D(P,r)\subset \Omega \), we have that
Then we say that \(f\) is superharmonic in \(\Omega \).
Suppose that \(f\) is a continuous, real-valued function in an open set \(\Omega \subseteq \C \). If \(f\) is both subharmonic and superharmonic, what can you say about \(f\)? Is the converse true?
Suppose that \(\alpha \in \R \setminus \{0\}\) and that \(f\), \(g\) are subharmonic and \(h\) is superharmonic in an open set \(\Omega \subseteq \C \). What can you say about the following functions:
Suppose that \(u\) and \(v\) are both subharmonic in an open set \(\Omega \). Let \(f(z)=\max (u(z),v(z))\). Show that \(f\) is subharmonic in \(\Omega \). (In particular, if \(u\) and \(v\) are real and harmonic then \(f\) is subharmonic.)
Let \(\overline D(P,r)\subset \Omega \). Without loss of generality we have that \(f(P)=u(P)\). Then\begin{align*} f(P)&=u(P)\leq \frac {1}{2\pi } \int _0^{2\pi } u(P+re^{i\theta })\,d\theta \end{align*}because \(u\) is subharmonic. But \(u(P+re^{i\theta })\leq \max (u(P+re^{i\theta }),v(P+re^{i\theta }))=f(P+re^{i\theta })\) by definition of maximum, and so
\begin{equation*}\int _0^{2\pi } u(P+re^{i\theta })\,d\theta \leq \int _0^{2\pi } f(P+re^{i\theta })\,d\theta .\end{equation*}Combining the two estimates yields that
\begin{equation*}f(P) \leq \frac {1}{2\pi } \int _0^{2\pi } f(P+re^{i\theta })\,d\theta .\end{equation*}This is true for all \(P\in \Omega \) and all \(r>0\) such that \(\overline D(P,r)\subset \Omega \), so \(f\) is subharmonic in \(\Omega \).
Let \(\Omega \subset \C \) be open and let \(f:\Omega \to \C \) be holomorphic. Show that \(u(z)=\abs {f(z)}\) is subharmonic in \(\Omega \).
By the Cauchy integral formula (Theorem 2.4.2), if \(\overline D(P,r)\subset \Omega \) then\begin{equation*}f(P)=\frac {1}{2\pi i} \oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}By definition of line integral
\begin{equation*}f(P)=\frac {1}{2\pi } \int _{0}^{2\pi } f(P+re^{i\theta })\,d\theta .\end{equation*}By Proposition 2.1.7, we have that
\begin{align*}|f(P)| &=\frac {1}{2\pi } \biggl |\int _{0}^{2\pi } f(P+re^{i\theta })\,d\theta \biggr | \leq \frac {1}{2\pi } \int _{0}^{2\pi } |f(P+re^{i\theta })|\,d\theta \end{align*}and so \(|f|\) is subharmonic.
[Jensen’s inequality] Let \(\varphi :\R \to \R \) be nondecreasing and convex, so that if \(0<t<1\) and \(a\), \(b\in \R \) then \(\varphi (ta+(1-t)b)\leq t\varphi (a)+(1-t)\varphi (b)\). If \(f:[a,b]\to \R \) is nonnegative and continuous (or more generally Lebesgue measurable), then
Let \(\Omega \subset \C \) be open and let \(u:\Omega \to \C \) be subharmonic. Let \(\varphi :\R \to \R \) be nondecreasing and convex, so that if \(0<t<1\) and \(a\), \(b\in \R \) then \(\varphi (ta+(1-t)b)\leq t\varphi (a)+(1-t)\varphi (b)\). Show that \(v(z)=\varphi (u(z))\) is subharmonic in \(\Omega \).
Suppose that \(\overline D(P,r)\subset \Omega \). Because \(\varphi \) is nondecreasing and \(u\) is subharmonic, we have that\begin{equation*}v(P)=\varphi (u(P))\leq \varphi \biggl (\frac {1}{2\pi }\int _0^{2\pi } u(P+re^{i\theta })\,d\theta \biggr ).\end{equation*}By Jensen’s inequality,
\begin{align*}\varphi \biggl (\frac {1}{2\pi }\int _0^{2\pi } u(P+re^{i\theta })\,d\theta \biggr ) &\leq \frac {1}{2\pi }\int _0^{2\pi } \varphi (u(P+re^{i\theta }))\,d\theta \\&=\frac {1}{2\pi }\int _0^{2\pi } v(P+re^{i\theta })\,d\theta . \end{align*}This completes the proof.
If \(u\) is harmonic and \(\varphi \) is convex, then \(\varphi \circ u\) is subharmonic even if \(\varphi \) is not nondecreasing.
Give an example of a function that is subharmonic in a domain \(\Omega \) but is not harmonic in that domain.
Let \(\Omega =\C \) and let \(f(z)=|z|^2=|z^2|\). Then \(f\) is subharmonic in \(\C \) by 4540Problem 4540. But \(f\) is not harmonic in \(\C \) because \(f(0)\leq f(z)\) for all \(z\in \C \) and \(f\) is not constant, and so \(f\) cannot satisfy the minimum principle; by 4090Problem 4090 this implies \(f\) cannot be harmonic.As another example, let \(g(z)=\max (\re z,\im z)\). Then \(g\) is subharmonic by 4040Problem 4040, 4041Problem 4041, and 4530Problem 4530, but \(g\) is not a \(C^2\) function and so cannot be harmonic.
Subharmonic functions satisfy the maximum principle. That is, suppose that \(\Omega \subseteq \C \) is open and connected, that \(f:\Omega \to \R \) is subharmonic, and that there is a \(P\in \Omega \) such that \(f(P)\geq f(z)\) for all \(z\in \Omega \). Then \(f\) is constant in \(\Omega \).
Prove the following generalization of Proposition 7.7.7: let \(\Omega \subseteq \C \) be open and connected. Suppose that \(f:\Omega \to \R \) is continuous and satisfies the small circle sub-mean-value property: for every \(P\in \Omega \), there is some \(\varepsilon _P>0\) such that \(D(P,\varepsilon _P)\subset \Omega \) and such that
Show that \(f\) satisfies the maximum principle in \(\Omega \): if there is a \(P\in \Omega \) such that \(f(P)\geq f(z)\) for all \(z\in \Omega \), then \(f\) is constant in \(\Omega \).
Show that there is no minimum principle for subharmonic functions.
For example, the subharmonic function \(|z|\) has a minimum at \(z=0\) but is not constant.
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \R \) be continuous. Then \(f\) is subharmonic (in the sense given in these lecture notes) if and only if, whenever \(\overline D(P,r)\subset \Omega \), \(h\) is harmonic in \(D(P,r)\) and continuous on \(\overline D(P,r)\), and \(h\geq f\) on \(\partial D(P,r)\), we have that \(h\geq f\) in \(D(P,r)\). (Note that this second characterization is a bit stronger than the version given in the book, and so the proof is correspondingly simpler.)
Begin the proof of Proposition 7.7.4 as follows. Suppose that \(\Omega \subseteq \C \) is open and that \(f:\Omega \to \R \) is continuous. Suppose further that whenever \(\overline D(P,r)\subset \Omega \), \(h\) is harmonic in \(D(P,r)\) and continuous on \(\overline D(P,r)\), and \(h\geq f\) on \(\partial D(P,r)\), we have that \(h\geq f\) in \(D(P,r)\). Prove that \(f\) is subharmonic in the sense that \(f\) satisfies the sub-mean-value property
whenever \(\overline D(P,r)\subset \Omega \).
Suppose that \(\overline D(P,r)\subset \Omega \). Then \(f\big \vert _{\partial D(P,r)}\) is continuous. Let \(h\) be the function given by Theorem 7.3.4 (or rather 4230Problem 4230). Then \(h\) is continuous on \(\overline D(P,r)\), harmonic in \(D(P,r)\), and satisfies \(h=f\big \vert _{\partial D(P,r)}\) (that is, \(h=f\)) on \(\partial D(P,r)\). Thus \(f(P)\leq h(P)\).But by the mean value property for harmonic functions, or rather by 4110Problem 4110, we have that
\[h(P)=\frac {1}{2\pi }\int _0^{2\pi } h(P+re^{i\theta })\,d\theta =\frac {1}{2\pi }\int _0^{2\pi } f(P+re^{i\theta })\,d\theta .\]This completes the proof.
Complete the proof of Proposition 7.7.4 and strengthen the result as follows. Let \(\Omega \subseteq \C \) be open. Suppose that \(f:\Omega \to \R \) is continuous and satisfies the small circle sub-mean-value property in \(\Omega \) (as in Problem 7.79a). Show that whenever \(\overline D(P,r)\subset \Omega \), \(h\) is harmonic in \(D(P,r)\) and continuous on \(\overline D(P,r)\), and \(h\geq f\) on \(\partial D(P,r)\), we have that \(h\geq f\) in \(D(P,r)\). Hint: Use the maximum principle for solutions satisfying the small-circle sub-mean-value property.
Choose some such \(P\), \(r\), and \(h\). Then \(f-h\) satisfies the small circle sub-mean-value property because \(h\) satisfies the full mean value property. Therefore, by Problem 7.79a, we have that \(f-h\) satisfies the maximum principle. Because \(\overline D(P,r)\) is compact, this implies that \(\sup _{D(P,r)}(f-h)\leq \max _{\partial D(P,r)}(f-h)\leq 0\), as desired.
Let \(\Omega \subsetneq \C \) be a nonempty connected open set. We say that the Dirichlet problem is well posed on \(\Omega \) if, for every function \(f\) defined and continuous on \(\partial \Omega \), there is exactly one function \(u\) that is harmonic in \(\Omega \), continuous on \(\overline \Omega \), and such that \(u=f\) on \(\partial \Omega \).
Give an example of an unbounded domain \(\Omega \) and two distinct functions \(u\) and \(v\) that are harmonic in \(\Omega \), continuous on \(\overline \Omega \) and equal zero on \(\partial \Omega \).
Let \(\Omega =\{z\in \C :\re z>0\}\), let \(u(z)=0\), and let \(v(z)=\im z\). It is straightforward to verify that \(u\), \(v\), and \(\Omega \) satisfy the desired conditions.
Prove that we have uniqueness for the Dirichlet problem in any bounded domain; that is, show that if \(\Omega \subsetneq \C \) is bounded, if \(u\) and \(v\) are both harmonic in \(\Omega \) and continuous on \(\overline \Omega \), and if \(u=v\) on \(\partial \Omega \), then \(u=v\) in \(\Omega \). Clearly explain how you used the fact that \(\Omega \) is bounded.
Let \(0<r<1\). Let \(u(z)=\frac {1}{\log r}\log |z|\). Show that \(u\) is harmonic in the annulus \(\Omega =D(0,1)\setminus D(0,r)\), continuous on \(\overline \Omega \), and satisfies \(u(e^{i\theta })=0\), \(u(re^{i\theta })=1\) for any \(0\leq \theta \leq 2\pi \).
Let \(\Omega =D(0,1)\setminus \{0\}\). Suppose that \(u\) is harmonic in \(\Omega \), continuous on \(\overline \Omega \), and that \(u=0\) on \(\partial D(0,1)\). Prove that \(u(0)=0\). Is the Dirichlet problem well posed in \(\Omega \)?
Let \(\Omega \subsetneq \C \) be open and let \(P\in \partial \Omega \). Suppose that the function \(b:\overline \Omega \to \R \) has the following properties.
Then we say that \(b\) is a barrier for \(\Omega \) at \(P\).
Let \(\Omega \subset \C \) be a nonempty bounded connected open set. The Dirichlet problem is well posed in \(\Omega \) if and only if, for every \(P\in \partial \Omega \), there is a function \(b_P\) that is a barrier for \(\Omega \) at \(P\).
If \(b\) is a barrier for \(\Omega \) at \(P\), show that \(b(z)<0\) for all \(z\in \Omega \).
The function \(b(z)=\re z-1\) is a barrier for \(\D \) at \(1\).
Let \(\Omega \subsetneq \C \) be a nonempty bounded open set. Let \(P\in \partial \Omega \) satisfy \(|P|\geq |z|\) for all \(z\in \overline \Omega \). Then the function \(b(z)=\re (\frac {1}{P}z)-1\) is a barrier for \(\Omega \) at \(P\).
Suppose that \(\Omega \subsetneq \C \) is open and \(P\in \partial \Omega \). Suppose that there is an \(r>0\) such that there exists a barrier \(b_1\) for \(\Omega \cap D(P,r)\) at \(P\). If \(\varepsilon >0\) is small enough, then the function
is a barrier for \(\Omega \) at \(P\).
Prove that the function \(b_2\) in Example 7.7.12 is indeed a barrier for \(\Omega \) at \(P\).
State and prove the converse to Example 7.7.12.
Show that there is a barrier for the domain \(\Omega =\C \setminus [0,\infty )=\{re^{i\theta }:r>0,\> 0<\theta <2\pi \}\) at the point \(P=0\).
If \(\Omega \subsetneq \C \) is an open set, \(P\in \partial \Omega \), and \(\C \setminus \Omega \) contains a line segment with one end point at \(P\), then there exists a barrier for \(\Omega \) at \(P\).
Show that the barrier of Example 7.7.11 exists. You don’t have to give an explicit formula for the barrier.
Let \(\Omega =\D \setminus \{0\}\). Show that there is no barrier for \(\Omega \) at \(0\). Hint: Suppose that \(b\) satisfies all of the properties of a barrier except that \(b(0)\leq 0\) instead of \(b(0)=0\). Show that \(b\) may be bounded above by a suitable modification of the harmonic function in 4620Problem 4620 and see what you can conclude about \(b\).
Let \(\Omega \subset \C \) be a nonempty bounded connected open set. The Dirichlet problem is well posed in \(\Omega \) if and only if, for every \(P\in \partial \Omega \), there is a function \(b_P\) that is a barrier for \(\Omega \) at \(P\).
Prove the “only if” direction of Theorem 7.8.1: Suppose that the Dirichlet problem is well posed in \(\Omega \) and \(P\in \partial \Omega \) and construct a barrier for \(\Omega \) at \(P\).
Let \(\Omega \subset \C \) be a nonempty bounded connected open set and let \(f:\partial \Omega \to \R \) be continuous. Let \(M=\max _{\partial \Omega } |f|\). Let
where \(C^0(\overline \Omega )\) is the set of all continuous functions on \(\overline \Omega \). Then:
Let \(S\), \(f\), \(\Omega \) be as in 4710Problem 4710 and define
Then \(-M\leq u(z)\leq M\) (and \(u(z)\) exists) for all \(z\in \overline \Omega \). Show that \(u(P)\leq f(P)\) for all \(P\in \partial \Omega \).
Let \(P\in \partial \Omega \) and let \(b_P\) be a barrier for \(\Omega \) at \(P\). Let \(\varepsilon >0\). Show that there exists a \(C>0\) large enough that
for all \(z\in \partial \Omega \).
Let \(P\in \partial \Omega \) and let \(\varepsilon >0\). Show that there is a \(\delta >0\) such that if \(|z-P|<\delta \) and \(z\in \overline \Omega \) then \(u(z)>f(P)-\varepsilon \). (This implies in particular that \(u(P)=f(P)\) but also implies that \(u\) is lower semicontinuous at \(P\).)
Show that \(u\) is continuous at \(P\) for all \(P\in \partial \Omega \).
Let \(\psi \in S\) and let \(\overline D(P,r)\subset \Omega \). Define
Show that \(\varphi \) is also in \(S\) and that \(\varphi (\zeta )\geq \psi (\zeta )\) for all \(\zeta \in \overline \Omega \).
Let \(\overline D(P,r)\subset \Omega \) for some \(r>0\). For each \(w\in D(P,r)\), show that there is a sequence of functions \(\{\varphi _{w,n}\}_{n=1}^\infty \), all of which are in \(S\), harmonic in \(D(P,r)\), and nondecreasing on \(\Omega \), such that \(u(w)=\lim _{n\to \infty } \varphi _{w,n}(w)\).
For each \(w\), \(z\in D(P,r)\), show that there is a sequence of functions \(\{\varphi _{w,z,n}\}_{n=1}^\infty \), all of which are in \(S\), harmonic in \(D(P,r)\), and nondecreasing on \(\Omega \), such that \(u(w)=\lim _{n\to \infty } \varphi _{w,z,n}(w)\), \(u(z)=\lim _{n\to \infty } \varphi _{w,z,n}(z)\), and if \(\zeta \in \Omega \) then \(\varphi _{z,w}(\zeta )\geq \varphi _z(\zeta )\) and \(\varphi _{z,w}(\zeta )\geq \varphi _w(\zeta )\).
(Harnack’s principle.) Let \(\{u_k\}_{k=1}^\infty \) be a sequence of real-valued functions harmonic in a connected open set \(\Omega \subseteq \C \) such that \(u_1(z)\leq u_2(z)\leq u_3(z)\leq \cdots \) for each \(z\in \Omega \). Then either \(u_k\to \infty \) uniformly on compact sets or there is a harmonic function \(u:\Omega \to \R \) such that \(u_k\to u\) uniformly on compact sets.
If \(w\), \(z\in D(P,r)\), let
Then \(u_w\) and \(u_{z,w}\) are both harmonic in \(D(P,r)\). Show that \(u_w(\zeta )=u_{z,w}(\zeta )\) for all \(\zeta \in D(P,r)\).
Complete the proof of Theorem 7.8.1.
(The Bolzano-Weierstraß theorem.) Suppose that \(\{z_n\}_{n=1}^\infty \subset \R ^d\) is bounded. Then there is a subsequence \(\{z_{n_k}\}_{k=1}^\infty \) that converges as \(k\to \infty \).
Let \(\Omega \), \(W\subsetneq \C \) be two bounded open sets. Suppose that there exists some continuous bijection \(\varphi :\Omega \to W\) with a continuous inverse. Let \(z_\infty \in \partial \Omega \). Let \(\{z_n\}_{n=1}^\infty \subset \Omega \) with \(z_n\to z_\infty \). Then \(\{\varphi (z_n)\}_{n=1}^\infty \subset W\) is bounded, so by the Bolzano-Weierstraß theorem there is a subsequence \(\{z_{n_k}\}_{k=1}^\infty \) such that \(\varphi (z_{n_k})\) converges. Show that \(\varphi (z_{n_k})\) converges to a point in \(\partial W\).
Let \(0<r_1<R_1<\infty \) and \(0<r_2<R_2<\infty \). Let \(P_1\in \C \) and \(P_2\in \C \). Let \(A_1=\{z\in \C :r_1<\abs {z-P_1}<R_1\}\) and \(A_2=\{z\in \C :r_2<\abs {z-P_2}<R_2\}\). Then \(A_1\) and \(A_2\) are conformally equivalent (meaning that there is a holomorphic bijection \(\varphi :A_1\to A_2\)) if and only if \(R_1/r_1=R_2/r_2\).
Let \(A=\{z\in \C : 1/R<\abs {z}<R\}\) be an annulus for some \(R>1\). Find all conformal self-maps of \(A\).
Prove the straightforward direction of Theorem 7.9.1; that is, assume \(R_1/r_1=R_2/r_2\) and prove that \(A_1\) and \(A_2\) are conformally equivalent.
Let
for some \(0<r_1<R_1<\infty \), \(0<r_2<R_2<\infty \). Suppose that \(\varphi :A_1\to A_2\) is a holomorphic bijection.
Let \(\{z_n\}_{n=1}^\infty \subset A_1\) and \(\{\zeta _m\}_{m=1}^\infty \subset A_1\) with
By passing to subsequences, we may assume that \(\{\varphi (z_n)\}_{n=1}^\infty \) and \(\{\varphi (\zeta _m)\}_{m=1}^\infty \) also converge. By 4820Problem 4820,
We then have that
We now begin the proof of 4840Lemma 4840. Let \(r_2<\rho <R_2\). Let \(s_\rho =\sup \{\abs {\varphi ^{-1}(\rho e^{i\theta })}:0\leq \theta \leq 2\pi \}\). Show that \(r_1< s_\rho <R_1\).
Let \(r_2<\rho <R_2\). Let \(\Omega _{\rho }^-=\{z\in A_1:|\varphi (z)|<\rho \}\) and let \(\Omega _{\rho }^+=\{z\in A_1:|\varphi (z)|>\rho \}\). Show that \(\Omega _\rho ^+\) and \(\Omega _\rho ^-\) are disjoint connected open sets.
Suppose that \(|\varphi (z_{n})|\to R_2\). Show that \(\abs {\varphi (z)}>\rho \) for all \(z\in A_1\) with \(\abs {z}>s_\rho \).
Suppose that \(|\varphi (z_{n})|\to R_2\). Show that \(\lim _{z\to w} |\varphi (z)|=R_2\) for all \(w\in \partial D(0,R_1)\).
We can similarly prove the other three cases of 4840Lemma 4840.
Let \(\Omega \subseteq \C \) be open and let \(f:\Omega \to \C \setminus \{0\}\) be holomorphic. Show that \(u(z)=\log |f(z)|\) is harmonic in \(\Omega \). (Note that \(\Omega \) may not be simply connected, and so Lemma 6.6.4 cannot be applied in \(\Omega \).)
Let \(A_1\), \(A_2\), and \(\varphi \) be as in 4840Lemma 4840. Let \(u(z)=\log |\varphi (z)|\) for all \(z\in A_1\), \(u(z)=\lim _{\zeta \to z}|\varphi (\zeta )|\) for all \(z\in \partial A_1\). Then \(u\) is continuous on \(\overline {A_1}\) and harmonic in \(A_1\). Show that there exist constants \(\alpha \) and \(\beta \) such that
for all \(z\in \overline {A_1}\).
Let \(\Omega =A_1\setminus (-\infty ,0)\) be the annulus with the negative real numbers deleted. Then the function \(\log \) can be defined such that it is holomorphic on \(\Omega \). Show that there is a \(\omega \in \C \) such that \(\varphi (z)=\omega e^{\beta \log z}\) for all \(z\in \Omega \), where \(\beta \) is as in the previous problem.
Given that \(\varphi \) is continuous on \(A_1\) (and so continuous up to the negative reals), what must be true about the number \(\beta \)? Given that \(\varphi \) is injective on \(A_1\) (and in particular on \(\{e^{i\theta }:-\pi <\theta \leq \pi \}\)), what must be true about the number \(\beta \)?
Prove Theorem 7.9.1.
If \(f\) is a fractional linear transformation, \(c\) and \(C\) are concentric circles, and \(f(c)\) and \(f(C)\) are also concentric circles, then the ratio of the radii of \(c\) and \(C\) is equal to the ratio of the radii of \(f(c)\) and \(f(C)\).
1. Some authors, especially in physics, write \(z^*\) instead of \(\bar z\) for the complex conjugate of \(z\).
2. This means that \(\gamma (0)=\gamma (1)\), \(\gamma (t)\neq \gamma (s)\) for any \(t\neq s\) except \(0\) and \(1\), and there are finitely many points \(0=t_0<t_1<\dots <t_n=1\) such that if \(1\leq k\leq n\) then \(\gamma '(t)\) exists for all \(t\in (t_{k-1},t_k)\), is continuous on \((t_{k-1},t_k)\), and has right and left limits, respectively, at \(t_{k-1}\) and \(t_k\).
3. Occasionally it is convenient to allow \(f\) to also have removable singularities at points of \(S\); we can however take the convention that all removable singularities should be removed using the Riemann removable singularities theorem.
4. We may weaken the condition that \((Y,\rho )\) be compact to the condition that all closed and bounded subsets of \((Y,\rho )\) are compact if we in addition impose the condition that if \(z\in \Psi \), then \(\{f_n(z):n\in \N \}\) is bounded.