\( \newcommand{\C}{\mathbb{C}} \newcommand{\R}{\mathbb{R}} \newcommand{\F}{\mathbb{F}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\D}{\mathbb{D}} \def\H{\mathbb{H}} \newcommand{\mult}{\mathop{\mathrm{mult}}\nolimits} \renewcommand{\L}{{\mathcal{L}}} \newcommand{\B}{{\mathcal{B}}} \newcommand{\A}{{\mathcal{A}}} \newcommand{\M}{{\mathcal{M}}} \renewcommand{\S}{{\mathcal{S}}} \newcommand{\T}{{\mathcal{T}}} \newcommand{\dist}{\mathop{\mathrm{dist}}\nolimits} \newcommand{\Null}{\mathop{\mathrm{null}}\nolimits} \newcommand{\Span}{\mathop{\mathrm{span}}\nolimits} \newcommand{\re}{\mathop{\mathrm{Re}}\nolimits} \newcommand{\Ind}{\mathop{\mathrm{Ind}}\nolimits} \newcommand{\Res}{\mathop{\mathrm{Res}}\nolimits} \newcommand{\esssup}{\mathop{\mathrm{ess\,sup}}} \newcommand{\im}{\mathop{\mathrm{Im}}\nolimits} \newcommand{\Int}{\mathop{\mathrm{int}}\nolimits} \newcommand{\graph}{\mathop{\mathrm{graph}}\nolimits} \newcommand{\arccot}{\mathop{\mathrm{arccot}}\nolimits} \newcommand{\myallowbreak}{} \newcommand\p[2][]{\frac{\partial #1}{\partial #2}} \newcommand\sgn{\mathop{\mathrm{sgn}}\nolimits} \newcommand\cl{\mathop{\mathrm{cl}}\nolimits} \newcommand\abs[1]{|#1|} \)

1.1. Elementary Properties of the Complex Numbers

[Definition: The complex numbers] The set of complex numbers is $\R ^2$, denoted $\C $. (In this class, you may use everything you know about $\R $ and $\R ^2$—in particular, that $\R ^2$ is an abelian group and a normed vector space.)

[Definition: Real and imaginary parts] If $(x,y)$ is a complex number, then $\re (x,y)=x$ and $\im (x,y)=y$.

[Definition: Addition and multiplication] If $(x,y)$ and $(\xi ,\eta )$ are two complex numbers, we define

\begin{align*} (x,y)+(\xi ,\eta )&=(x+\xi ,y+\eta ),\\ (x,y)\cdot (\xi ,\eta )&=(x\xi -y\eta ,x\eta +y\xi ). \end{align*}

(Fact 20) This notion of addition and multiplication makes the complex numbers a ring—thus, multiplication is also associative and distributes over addition.

(Problem 40) Let $r$ be a real number. Recall that $\C =\R ^2$ is a vector space over $\R $, so we can multiply vectors (complex numbers) by scalars (real numbers). Is there a complex number $(\xi ,\eta )$ such that $r(x,y)=(\xi ,\eta )\cdot (x,y)$ for all $(x,y)\in \C $?

(Problem 60) If $z=x+iy$ for $x$, $y$ real, what are $\re z$ and $\im z$?

(Problem 70) If $z\in \C $ and $r$ is real, what are $\re (zr)$ and $\im (zr)$?

(Problem 80) If $z$, $w\in \C $, what are $\re (zw)$, $\im (zw)$ in terms of $\re z$, $\re w$, $\im z$, and $\im w$?

[Definition: Conjugate] The conjugate to the complex number $x+iy$, where $x$, $y$ are real, is $\overline {x+iy}=x-iy$.1

(Problem 90) If $z$ and $w$ are complex numbers, show that $\overline z+\overline w=\overline {z+w}$.

(Problem 110) Write $\re z$ and $\im z$ in terms of $z$ and $\overline z$.

(Problem 120) Show that $z\overline {z}$ is always real and nonnegative. If $z\overline {z}=0$, what can you say about $z$?

(Problem 130) If $z$ is a complex number with $z\neq 0$, show that there exists another complex number $w$ such that $zw=1$. Give a formula for $w$ in terms of $z$. We will write $w=\frac {1}{z}$.

[Definition: Modulus] If $z$ is a complex number, we define its modulus $|z|$ as $|z|=\sqrt {z\overline z}$.

(Fact 140) $|\re z|\leq |z|$ and $|\im z|\leq |z|$ (where the first $|\,\cdot \,|$ denotes the absolute value in the real numbers and the second $|\,\cdot \,|$ denotes the modulus in the complex numbers.)

(Problem 150) If $z$ and $w$ are complex numbers, show that $|zw|=|z|\,|w|$.

(Problem 160) Give an example of a non-constant polynomial that has no roots (solutions) that are real numbers. Find a root (solution) to your polynomial that is a complex number.

1.2. Real Analysis

(Fact 170) If $z=x+iy=(x,y)$, then the complex modulus $|z|$ is equal to the vector space norm $\|(x,y)\|$ in $\R ^2$.

(Fact 180) $\C $ is complete as a metric space if we use the expected metric $d(z,w)=|z-w|$.

(Problem 190) Recall that $(\R ^2,d)$ is a metric space, where $d(u,v)=\|u-v\|$. In particular, this metric satisfies the triangle inequality. Write the triangle inequality as a statement about moduli of complex numbers. Simplify your statement as much as possible.

(Memory 200) If $\{a_n\}_{n=1}^\infty $ is a sequence of points in $\R ^p$, $a\in \R ^p$, and we write $a_n=(a_n^1,a_n^2,\dots ,a_n^p)$, $a=(a^1,\dots a^p)$, then $a_n\to a$ (in the metric space sense) if and only if $a_n^k\to a^k$ for each $1\leq k\leq p$.

[Definition: Maclaurin series] If $f:\R \to \R $ is an infinitely differentiable function, the Maclaurin series for $f$ is the power series

\begin{equation*}\sum _{n=0}^\infty \frac {f^{(n)}(0)}{n!}x^n\end{equation*}

(Memory 220) The Maclaurin series for the $\exp $ function is $\sum _{k=0}^\infty \frac {x^k}{k!}$.

(Memory 230) The Maclaurin series for the $\sin $ function is $\sum _{k=0}^\infty (-1)^{k}\frac {x^{2k+1}}{(2k+1)!}$.

(Memory 240) The Maclaurin series for the $\cos $ function is $\sum _{k=0}^\infty (-1)^{k}\frac {x^{2k}}{(2k)!}$.

(Memory 250) If $x$ is real, then the Maclaurin series for $\exp x$, $\sin x$, or $\cos x$ converges to $\exp x$, $\sin x$, or $\cos x$, respectively.

\begin{align*} \sin (x+t)&=\sin x\cos t+\sin t\cos x,\\ \cos (x+t)&=\cos x\cos t-\sin x\sin t.\end{align*}

(Memory 270) The Cauchy-Schwarz inequality for real numbers states that if $n\in \N $ is a positive integer, and if for each $j$ with $1\leq j\leq n$ the numbers $x_j$, $\xi _j$ are real, then

\begin{equation*}\Bigl (\sum _{j=1}^n x_j\,\xi _j\Bigr )^2\leq \Bigl (\sum _{j=1}^n x_j^2 \Bigr )\Bigl (\sum _{j=1}^n \xi _j^2\Bigr ).\end{equation*}

1.2. Further Properties of the Complex Numbers

(Problem 280) State the Cauchy-Schwarz inequality for complex numbers and prove that it is valid.

(Problem 290) Let $z\in \C $. Consider the series $\sum _{j=0}^\infty \frac {z^j}{j!}$, that is, the sequence of complex numbers $\bigl \{\sum _{j=0}^n \frac {z^j}{j!}\bigr \}_{n=0}^\infty $. Show that this sequence is a Cauchy sequence.

(Problem 300) Since $\C $ is complete, the series converges. If $z=x$ is a real number, to what number does the series converge?

(Problem 310) If $z=iy$ is purely imaginary (that is, if $y\in \R $), show that $\sum _{j=0}^\infty \frac {(iy)^j}{j!}$ converges to $\cos y+i\sin y$.

(Bonus Problem 320) If $z=x+iy$, show that $\sum _{j=0}^\infty \frac {z^j}{j!}$ converges to the product $\bigl (\sum _{j=0}^\infty \frac {x^j}{j!}\bigr )\bigl (\sum _{j=0}^\infty \frac {(iy)^j}{j!}\bigr )$.

\begin{equation*}\exp (x)=\sum _{j=0}^\infty \frac {x^j}{j!}\quad \text { and }\quad \exp (ix)=\sum _{j=0}^\infty \frac {(ix)^j}{j!}.\end{equation*}

\begin{equation*}\exp (z)=\exp (x)\cdot \exp (iy).\end{equation*}

(Problem 330) If $y$, $\eta $ are real, show that $\exp (iy+i\eta )=\exp (iy)\cdot \exp (i\eta )$.

(Problem 340) If $z$, $w$ are any complex numbers, show that $\exp (z+w)=\exp (z)\cdot \exp (w)$.

(Problem 350) Suppose that $z$ is a complex number and that $|z|=1$. Show that there is a number $\theta \in \R $ with $\exp (i\theta )=z$. How many such numbers $\theta $ exist?

[Chapter 1, Problem 25] If $\theta $, $\varpi \in \R $, then $e^{i\theta }=e^{i\varpi }$ if and only if $(\theta -\varpi )/(2\pi )$ is an integer.

(Problem 360) Suppose that $z$ is a complex number. Show that there exist numbers $r\in [0,\infty )$ and $\theta \in \R $ such that $z=r\exp (i\theta )$. How many possible values of $r$ exist? How many possible values of $\theta $ exist?

1.3. Real Analysis

(Problem 380) Give an example of a function that can be written in two different ways.

[Definition: Ring of polynomials] Let $\R [z]$ be the ring of polynomials in one variable with real coefficients, that is,

\begin{equation*}\R [z]=\bigl \{p:p(z)=\sum _{k=0}^n a_k\,z^k\text { for some } n\in \N _0,a_k\in \R \bigr \}.\end{equation*}

Let $\R [x,y]$ be the ring of polynomials in two variables with real coefficients, that is,

\begin{equation*}\R [x,y]=\bigl \{p:p(x,y)=\sum _{j=0}^n\sum _{k=0}^n a_{j,k}\,x^j\,y^k\text { for some } n\in \N _0,a_{j,k}\in \R \bigr \}.\end{equation*}

[Definition: Degree] If $p\in \R [z]$ and $p(z)=\sum _{k=0}^n a_k\,z^k$, then the degree of $p$ is the largest nonnegative integer $m$ such that $a_m\neq 0$. (The degree of the zero polynomial $p(z)=0$ is either undefined, $-1$, or $-\infty $.)

(Problem 390) Let $p(x)=\sum _{k=0}^n a_k\,x^k$ and let $q(x)=\sum _{k=0}^n b_k\,x^k$ be two polynomials in $\R [x]$, with $a_k$, $b_k\in \R $. Show that if $p(x)=q(x)$ for all $x\in \R $ then $a_k=b_k$ for all $k\in \N _0$.

(Problem 400) Let $p\in \R [x]$ be a polynomial. Suppose that $x_0\in \R $ and that $p(x_0)=0$. Show that there exists a polynomial $q\in \R [x]$ such that $p(x)=(x-x_0)q(x)$ for all $x\in \R $. Further show that, if $p$ is a polynomial of degree $m\geq 0$, then $q$ is a polynomial of degree $m-1$. Hint: Use induction.

(Problem 410) Let $p(x)=\sum _{k=0}^n a_k\,x^k$ and let $q(x)=\sum _{k=0}^n b_k\,x^k$ be two polynomials of degree at most $n$ in $\R [x]$, with $a_k$, $b_k\in \R $ and $n\in \N _0$. Suppose that there are $n+1$ distinct numbers $x_0,x_1,\dots ,x_n\in \R $ such that $p(x_j)=q(x_j)$ for all $0\leq j\leq n$. Show that $a_k=b_k$ for all $k\in \N _0$. Hint: Consider the polynomial $r(x)=p(x)-q(x)$.

(Problem 420) Let $p(x,y)=\sum _{j=0}^n\sum _{k=0}^n a_{j,k}\,x^j\,y^k$ and let $q(x,y)=\sum _{j=0}^n\sum _{k=0}^n b_{j,k}\,x^j\,y^k$ be two polynomials in $\R [x,y]$, with $a_{j,k}$, $b_{j,k}\in \R $. Show that if $p(x,y)=q(x,y)$ for all $(x,y)\in \R ^2$ then $a_{j,k}=b_{j,k}$ for all $j$, $k\in \N _0$.

(Memory 421) If $\Omega \subseteq \R ^2$ is both open and connected, then $\Omega $ is path connected: for every $z$, $w\in \Omega $ there is a continuous function $\gamma :[0,1]\to \Omega $ such that $\gamma (0)=z$ and $\gamma (1)=w$.

(Memory 422) If $\Omega \subseteq \R ^2$ is open and connected, we may require the paths in the definition of path connectedness to be $C^1$.

(Memory 423) If $\Omega \subseteq \R ^2$ is open and connected, we may require the paths in the definition of path connectedness to consist of finitely many horizontal or vertical line segments.

Definition 1.3.1 (part 1). Let $\Omega \subseteq \R ^2$ be open. Suppose that $f:\Omega \to \R $. We say that $f$ is continuously differentiable, or $f\in C^1(\Omega )$, if the two partial derivatives $\frac {\partial f}{\partial x}$ and $\frac {\partial f}{\partial y}$ exist everywhere in $\Omega $ and $f$, $\frac {\partial f}{\partial x}$, and $\frac {\partial f}{\partial y}$ are all continuous on $\Omega $.

(Problem 424) Let $B=B(z,r)$ be a ball in $\R ^2$. Let $f\in C^1(B)$ and suppose that $\frac {\partial f}{\partial y}=\frac {\partial f}{\partial x}=0$ everywhere in $B$. Show that $f$ is a constant.

(Problem 430) Suppose that $\Omega \subseteq \R ^2$ is open and connected. Let $f\in C^1(\Omega )$ and suppose that $\frac {\partial f}{\partial y}=\frac {\partial f}{\partial x}=0$ everywhere in $\Omega $. Show that $f$ is a constant.

1.3. Complex Polynomials

[Definition: Ring of polynomials] Let $\C [z]$ be the ring of polynomials in one variable with complex coefficients, that is,

\begin{equation*}\C [z]=\bigl \{p:p(z)=\sum _{k=0}^n a_k\,z^k\text { for some } n\in \N _0,a_k\in \C \bigr \}.\end{equation*}

Let $\C [x,y]$ be the ring of polynomials in two variables with complex coefficients, that is,

\begin{equation*}\C [x,y]=\bigl \{p:p(x,y)=\sum _{j=0}^n\sum _{k=0}^n a_{j,k}\,x^j\,y^k\text { for some } n\in \N _0,a_{j,k}\in \C \bigr \}.\end{equation*}

(Problem 440) Let $p(z)=\sum _{k=0}^n a_k\,z^k$ and let $q(z)=\sum _{k=0}^n b_k\,z^k$ be two polynomials in $\C [z]$. Show that if $p(x)=q(x)$ for all $x\in \R $ then $a_k=b_k$ for all $k$, and so $p(z)=q(z)$ for all $z\in \C $.

(Problem 450) Show that Problems 400 and 410 are valid for polynomials in $\C [z]$ with complex roots.

(Problem 460) Let $p(z,w)=\sum _{j=0}^n\sum _{k=0}^n a_{j,k}\,z^j\,w^k$ and let $q(z,w)=\sum _{j=0}^n\sum _{k=0}^n b_{j,k}\,z^j\,w^k$ be two polynomials in $\C [z,w]$, with $a_{j,k}$, $b_{j,k}\in \C $. Show that if $p(x,y)=q(x,y)$ for all $(x,y)\in \R ^2$ then $a_{j,k}=b_{j,k}$ for all $j$, $k\in \N _0$.

(Problem 470) Let $p(z,w)=\sum _{j=0}^n\sum _{k=0}^n a_{j,k}\,z^j\,w^k$ and let $q(z,w)=\sum _{j=0}^n\sum _{k=0}^n b_{j,k}\,z^j\,w^k$ be two polynomials in $\C [z,w]$, with $a_{j,k}$, $b_{j,k}\in \C $. Show that if $p(z,\overline z)=q(z,\overline z)$ for all $z\in \C $ then $a_{j,k}=b_{j,k}$ for all $j$, $k\in \N _0$.

(Problem 480) Let $p\in \C [z,w]$ satisfy $p(z,\overline z)=z^2-\overline z^3$. Is there a polynomial $q\in \C [z]$ such that $q(z)=p(z,\overline z)$ for all $z\in \C $?

Definition 1.3.1 (part 2). Let $\Omega \subseteq \C $ be an open set. Recall $\C =\R ^2$. Let $f:\Omega \to \C $ be a function. Then $f\in C^1(\Omega )$ if $\re f$, $\im f\in C^1(\Omega )$.

[Definition: Derivative of a complex function] Let $f\in C^1(\Omega )$. Let $u(z)=\re f(z)$ and let $v(z)=\im f(z)$. Then

\begin{equation*}\frac {\partial f}{\partial x} = \frac {\partial u}{\partial x}+i\frac {\partial v}{\partial x}, \quad \frac {\partial f}{\partial y} = \frac {\partial u}{\partial y}+i\frac {\partial v}{\partial y}.\end{equation*}

\begin{equation*}\frac {\partial }{\partial x} (fg)=\frac {\partial f}{\partial x} g+f\frac {\partial g}{\partial x},\qquad \frac {\partial }{\partial y} (fg)=\frac {\partial f}{\partial y} g+f\frac {\partial g}{\partial y}\end{equation*}

1.3. The complex derivatives $\p {z}$ and $\p {\bar z}$

\begin{equation*}\frac {\partial f}{\partial z} = \frac {1}{2}\frac {\partial f}{\partial x}+\frac {1}{2i}\frac {\partial f}{\partial y}, \quad \frac {\partial f}{\partial \overline z} = \frac {1}{2}\frac {\partial f}{\partial x}-\frac {1}{2i}\frac {\partial f}{\partial y}.\end{equation*}

(Problem 500) Let $f(z)=z$. Show that $\frac {\partial f}{\partial z}=1$ and $\frac {\partial f}{\partial \overline z}=0$.

(Problem 510) Let $g(z)=\overline z$. Show that $\frac {\partial g}{\partial z}=0$ and $\frac {\partial g}{\partial \overline z}=1$.

(Problem 520) Show that $\frac {\partial }{\partial z}$ and $\frac {\partial }{\partial \overline z}$ are linear operators.

(Problem 530) Show that $\frac {\partial }{\partial z}$ and $\frac {\partial }{\partial \overline z}$ commute in the sense that, if $\Omega \subseteq \C $ is open and $f\in C^2(\Omega )$, then $\frac {\partial }{\partial z}\left (\frac {\partial }{\partial \overline z} f\right )=\frac {\partial }{\partial \overline z}\left (\frac {\partial }{\partial z} f\right )$.

\begin{equation*}\frac {\partial }{\partial z} (fg)=\frac {\partial f}{\partial z} g+f\frac {\partial g}{\partial z}, \qquad \frac {\partial }{\partial \overline z} (fg)=\frac {\partial f}{\partial \overline z} g+f\frac {\partial g}{\partial \overline z} .\end{equation*}

(Problem 550) Show that $\frac {\partial }{\partial z} (z^\ell \overline {z}^m)=\ell z^{\ell -1}\overline {z}^m$ and $\frac {\partial }{\partial \overline z} (z^\ell \overline {z}^m)=mz^\ell \overline {z}^{m-1}$ for all nonnegative integers $m$ and $\ell $.

(Problem 560) Let $j$, $k$, $\ell $, and $m$ be nonnegative integers. Find $\frac {\partial ^j}{\partial z^j} \frac {\partial ^k}{\partial \overline z^k} (z^\ell \overline {z}^m)$.

(Problem 570) Let $p\in \C [z,w]$. Show that there is a $q\in \C [z]$ such that $p(z,\overline z)=q(z)$ for all $z\in \C $ if and only if $\frac {\partial }{\partial \overline z}(p(z,\overline z))=0$ everywhere in $\C $.

(Problem 580) Let $p\in \C [x,y]$. Show that there is a $q\in \C [z]$ such that $p(x,y)=q(x+iy)$ for all $x$, $y\in \R $ if and only if $\frac {\partial }{\partial \overline z}(p(x,y))=0$ everywhere in $\C $.

(Problem 590) Suppose that $\Omega \subseteq \C $ is open and connected, that $f\in C^1(\Omega )$, and that $\frac {\partial f}{\partial z}=\frac {\partial f}{\partial \overline z}=0$ in $\Omega $. Show that $f$ is constant in $\Omega $.

(Problem 600) Suppose that $\Omega \subseteq \C $ is open and that $f\in C^1(\Omega )$. Show that

\begin{equation*}\frac {\partial f}{\partial z} = \overline {\left (\frac {\partial \overline f}{\partial \overline z}\right )}.\end{equation*}

(Problem 610) Show that $\frac {\partial }{\partial z}\frac {1}{z}=-\frac {1}{z^2}$ if $z\neq 0$.

(Problem 620) Show that $\frac {\partial }{\partial \overline z}\frac {1}{z}=0$ if $z\neq 0$.

(Problem 630) Find $\frac {\partial }{\partial z}\frac {1}{z^n}$ and $\frac {\partial }{\partial \overline z}\frac {1}{z^n}$ for any positive integer $n$.

[Chapter 1, Problem 49] Let $\Omega $, $W\subseteq \C $ be open and let $g:\Omega \to W$, $f:W\to \C $ be two $C^1$ functions. The following chain rules are valid:

\begin{gather*} \frac {\partial }{\partial z} (f\circ g)= \frac {\partial f}{\partial g}\frac {\partial g}{\partial z} +\frac {\partial f}{\partial \overline g}\frac {\partial \overline g}{\partial z}, \\ \frac {\partial }{\partial \overline z} (f\circ g)= \frac {\partial f}{\partial g}\frac {\partial g}{\partial \overline z} +\frac {\partial f}{\partial \overline g}\frac {\partial \overline g}{\partial \overline z}, \end{gather*}

where $\frac {\partial f}{\partial g} = \left .\frac {\partial f}{\partial z}\right |_{z\to g(z)}$, $\frac {\partial f}{\partial \overline g} = \left .\frac {\partial f}{\partial \overline z}\right |_{z\to g(z)}$.

1.4. Holomorphic Functions, the Cauchy-Riemann Equations, and Harmonic Functions

Definition 1.4.1. Let $\Omega \subseteq \C $ be open and let $f\in C^1(\Omega )$. We say that $f$ is holomorphic in $\Omega $ if

\begin{equation*} \frac {\partial f}{\partial \overline z}=0 \end{equation*}

Lemma 1.4.2. Let $f\in C^1(\Omega )$, let $u=\re f$, and let $v=\im f$. Then $f$ is holomorphic in $\Omega $ if and only if

\begin{equation*}\frac {\partial u}{\partial x}=\frac {\partial v}{\partial y}\quad \text {and}\quad \frac {\partial u}{\partial y}=-\frac {\partial v}{\partial x}\end{equation*}

everywhere in $\Omega $. (These equations are called the Cauchy-Riemann equations.)

(Problem 640) Prove the “only if” direction of Lemma 1.4.2: Suppose that $f$ is holomorphic in $\Omega $, $\Omega \subseteq \C $ open, then the Cauchy-Riemann equations hold for $u=\re f$ and $v=\im f$.

(Problem 650) Prove the “if” direction of Lemma 1.4.2: suppose that $u=\re f$ and $v=\im f$ are $C^1$ in $\Omega $ and satisfy the Cauchy-Riemann equations. Show that $f$ is holomorphic in $\Omega $.

Proposition 1.4.3. [Slight generalization.] Let $f\in C^1(\Omega )$. Then $f$ is holomorphic at $p\in \Omega $ if and only if $\frac {\partial f}{\partial x}(p)=\frac {1}{i}\frac {\partial f}{\partial y}(p)$ and that in this case

\begin{equation*}\frac {\partial f}{\partial z}(p)=\frac {\partial f}{\partial x}(p) =\frac {1}{i}\frac {\partial f}{\partial y}(p).\end{equation*}

(Problem 660) Begin the proof of Proposition 1.4.3 by showing that if $f$ is holomorphic then $\frac {\partial f}{\partial z}=\frac {\partial f}{\partial x}=\frac {1}{i}\frac {\partial f}{\partial y}$.

(Problem 670) Complete the proof of Proposition 1.4.3 by showing that if $f\in C^1(\Omega )$ and $\frac {\partial f}{\partial x}=\frac {1}{i}\frac {\partial f}{\partial y}$, then $f$ is holomorphic.

Definition 1.4.4. We let $\triangle =\frac {\partial ^2 }{\partial x^2}+\frac {\partial ^2 }{\partial y^2}$. If $\Omega \subseteq \C $ is open and $u\in C^2(\Omega )$, then $u$ is harmonic if

\begin{equation*}\triangle u=\frac {\partial ^2 u}{\partial x^2}+\frac {\partial ^2 u}{\partial y^2}=0\end{equation*}

(Problem 671) Show that if $f\in C^1(\Omega )$ then $\triangle f=4\frac {\partial }{\partial z}\frac {\partial f} {\partial \overline z} =4\frac {\partial }{\partial \overline z} \frac {\partial f}{\partial z}$.

(Problem 680) Suppose that $f$ is holomorphic and $C^2$ in an open set $\Omega $ and that $u=\re f$ and $v=\im f$. Compute $\triangle u$ and $\triangle v$.

(Problem 690) Let $f\in \C [z]$ be a holomorphic polynomial. Show that there is a polynomial $F\in \C [z]$ such that $\frac {\partial F}{\partial z} = f$. How many such polynomials are there?

Lemma 1.4.5. Let $u$ be harmonic and real valued in $\C $. Suppose in addition that $u\in \R [x,y]$, that is, that $u$ is a polynomial. Then there is a holomorphic polynomial $f\in \C [z]$ such that $u(x,y)=\re f(x+iy)$.

(Problem 700) Prove Lemma 1.4.5. Hint: Start by computing $\frac {\partial }{\partial z}\frac {\partial }{\partial \overline z}$ and $\frac {\partial }{\partial \overline z}\frac {\partial }{\partial z}$.

1.5. Real Analysis

(Memory 710) Let $a<c<b$ and let $f:(a,b)\to \R $ be continuous. Show that $\lim _{t\to 0} \frac {1}{t}\int _c^{c+t} f(x)\,dx=f(c)$.

(Memory 722) If $a<b$, if each $f_n$ is bounded and Riemann integrable on $[a,b]$, and if $f_n\to f$ uniformly on $[a,b]$, then $f$ is also Riemann integrable on $[a,b]$, $\lim _{n\to \infty } \int _a^b f_n$ exists, and $\int _a^b f = \lim _{n\to \infty } \int _a^b f_n$.

(Problem 723) Let $f:[a,b]\times [c,d]\to \R $. Suppose that $f$ is continuous on $[a,b]\times [c,d]$. Define $F:[a,b]\to \R $ by $F(x)=\int _{c}^d f(x,y)\,dy$. Show that $F$ is continuous on $[c,d]$.

(Problem 730) Let $f:(a,b)\times [c,d]\to \R $. Suppose that $f$ is continuous on $(a,b)\times [c,d]$ and the function $\partial _xf=\frac {\partial f}{\partial x}$ is continuous on $(a,b)\times [c,d]$. Show that

\begin{equation*}\frac {d}{dx} \int _c^d f(x,y)\,dy=\int _c^d \p {x} f(x,y)\,dy\end{equation*}

for all $a<x<b$. In particular, note that the derivative exists and the function $F(x)=\int _c^d f(x,y)\,dy$ is continuous on $(a,b)$.

(Fact 731) This is still true if $f$ is continuous on $[x,b)$ or $(a,x]$ and we extend $\partial _1 f$ to $(a,x]\times [c,d]$ or $[x,b)\times [c,d]$ by taking one-sided derivatives.

(Memory 740) Let $f$ be a $C^2$ function in an open set in $\R ^2$. Show that $\frac {\partial }{\partial x} \frac {\partial f}{\partial y}=\frac {\partial }{\partial y} \frac {\partial f}{\partial x}$.

1.5. Real and Holomorphic Antiderivatives

(Problem 750) Prove the converse. That is, suppose that there are two $C^1$ functions $g$ and $h$ defined in an open rectangle or disc $\mathcal {R}$ such that $\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h$ everywhere in $\mathcal {R}$. Show that there is a function $f\in C^2(\mathcal {R})$ such that $\frac {\partial f}{\partial y}=g$ and $ \frac {\partial f}{\partial x}=h$.

(Bonus Problem 760) State the definition of a simply connected set and then generalize Problem 750 to any simply connected open set.

(Problem 770) Let $\mathcal {R}=\R ^2\setminus \{(0,0)\}$. Let $g(x,y)=\frac {x}{x^2+y^2}$ and $h(x,y)=\frac {-y}{x^2+y^2}$. Show that $\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h$.

(Problem 780) Show that there is no function $f\in C^1(\mathcal {R})$ such that $\frac {\partial f}{\partial y}=g$ and $ \frac {\partial f}{\partial x}=h$.

(Problem 800) Suppose that $u$ is real-valued and harmonic (and not necessarily a polynomial) in an open rectangle or disc $\mathcal {R}$. Show that there is a function $f$ that is holomorphic in $\mathcal {R}$ such that $u=\re f$.

(Problem 810) Suppose that $f$ is holomorphic in an open rectangle or disc $\mathcal {R}$. Show that there is a function $F$ that is holomorphic in $\mathcal {R}$ such that $f=\frac {\partial F}{\partial z}$.

2.1. Real Analysis

(Memory 830) State the change of variables theorem for integrals over real intervals.

(Memory 840) Let $a<b$ and let $\varphi :[a,b]\to \R $ be continuous. Then $\left |\int _a^b \varphi \right |\leq \int _a^b |\varphi |\leq (b-a)\sup _{[a,b]}|\varphi |$.

[Definition: Continuous] Let $(X,d)$ and $(Z,\rho )$ be two metric spaces and let $f:X\to Z$. We say that $f$ is continuous at $x\in X$ if, for all $\varepsilon >0$, there is a $\delta >0$ such that if $d(x,y)<\delta $ and $y\in X$ then $\rho (f(x),f(y))<\varepsilon $.

(Memory 850) Let $X$ be a compact metric space and let $f:X\to Z$ be a continuous function. Then $f(X)$ is compact.

(Memory 860) Let $X$ be a compact metric space and let $f:X\to Z$ be a continuous bijection. Then $f^{-1}$ is also continuous.

(Memory 880) If $\gamma :X\to \R ^2$ and $\gamma (t)=(\gamma _1(t),\gamma _2(t))$ for all $t\in X$, then $\gamma $ is continuous if and only if $\gamma _1$ and $\gamma _2$ are continuous.

Definition 2.1.1. ($C^1$ on a closed set.) Let $[a,b]\subseteq \R $ be a closed bounded interval and let $f:[a,b]\to \R $. We say that $f\in C^1([a,b])$, or $f$ is continuously differentiable on $[a,b]$, if

(Memory 890) If the conditions (a), (b) and (c) hold, then the condition (d) holds if and only if the two limits $\lim _{t\to a^+} \frac {f(t)-f(a)}{t-a}$ and $\lim _{t\to b^-} \frac {f(b)-f(t)}{b-t}$ exist, and in this case $\lim _{t\to a^+} \frac {f(t)-f(a)}{t-a}=\lim _{t\to a^+} f'(t)$ and $\lim _{t\to b^-} \frac {f(b)-f(t)}{b-t}=\lim _{t\to b^-} f'(t)$.

[Definition: One-sided derivative] If $f:[a,b]\to \R $, we define $f'(a)=\lim _{t\to a^+} \frac {f(t)-f(a)}{t-a}$ and $f'(b)=\lim _{t\to b^-} \frac {f(b)-f(t)}{b-t}$, if these limits exist.

(Memory 900) Suppose that $a<p<b$ and let $H:(a,b)\to \R $ be continuous. Suppose that $H$ is differentiable on both $(a,p)$ and $(p,b)$, and that $\lim _{x\to p} H'(x)=h$ for some $h\in \R $. Then $H'(p)$ exists and that $H'(p)=\lim _{x\to p} H'(x)$.

[Definition: Curve] A curve in $\R ^2$ is a continuous function $\gamma :[a,b]\to \C $, where $[a,b]\subseteq \R $ is a closed and bounded interval. The trace (or image) of $\gamma $ is $\widetilde \gamma =\gamma ([a,b])=\{\gamma (t):t\in [a,b]\}$.

[Definition: Closed; simple] A curve $\gamma :[a,b]\to \R ^2$ is closed if $\gamma (a)=\gamma (b)$. A closed curve is simple if $\gamma (b)=\gamma (a)$ and $\gamma $ is injective on $[a,b)$ (equivalently on $(a,b]$).

[Definition: $C^1$ curve in $\R ^2$] A curve $\gamma :[a,b]\to \R ^2$ is $C^1$ (or continuously differentiable) if $\gamma (t)=(\gamma _1(t),\gamma _2(t))$ for all $t\in [a,b]$ and both $\gamma _1$, $\gamma _2$ are $C^1$. We write

\begin{equation*}\gamma '(t)=\frac {d\gamma }{dt}=\biggl (\frac {d\gamma _1}{dt},\frac {d\gamma _2}{dt}\biggr ).\end{equation*}

[Definition: Arc length] If $\gamma :[a,b]\to \R ^2$ is a $C^1$ curve, then its length (or arc length) is $\int _a^b \|\gamma '(t)\|\,dt$.

Proposition 2.1.4. Let $\gamma \in C^1([a,b])$, $\gamma :[a,b]\to \Omega $ for some open set $\Omega \subseteq \R ^2$ and let $f:\Omega \to \R $ with $f\in C^1(\Omega )$. Then

\begin{equation*}f(\gamma (b))-f(\gamma (a))=\int _a^b \frac {\partial f}{\partial x}\Big \vert _{(x,y)=\gamma (t)} \frac {\partial \gamma _1}{\partial t} +\frac {\partial f}{\partial y}\Big \vert _{(x,y)=\gamma (t)} \frac {\partial \gamma _2}{\partial t}\,dt.\end{equation*}

(Problem 910) Prove Proposition 2.1.4. Hint: Start by computing $\frac {d(f\circ \gamma )}{dt}$.

[Definition: Real line integral] Let $\gamma \in C^1([a,b])$, $\gamma :[a,b]\to \Omega $ for some open set $\Omega \subseteq \R ^2$ and $F:\Omega \to \R $ be continuous on $\Omega $. We define

\begin{equation*}\int _\gamma F\,ds=\int _a^b F(\gamma (t))\,\|\gamma '(t)\|\,dt.\end{equation*}

\begin{equation*}\int _\gamma \vec F\cdot \tau \,ds=\int _a^b \vec F(\gamma (t))\cdot \gamma '(t)\,dt\end{equation*}

2.1. Real and Complex Line Integrals

Definition 2.1.3. (Integral of a complex function.) If $f:[a,b]\to \C $, and both $\re f$ and $\im f$ are integrable on $[a,b]$, we define $\int _a^b f=\int _a^b\re f+i\int _a^b \im f$.

Proposition 2.1.7. Suppose that $a<b$ and that $f:[a,b]\to \C $ is continuous. Then $|\int _a^b f|\leq \int _a^b |f|\leq (b-a)\sup _{[a,b]}|f|$.

(Problem 920) Prove Proposition 2.1.7. Hint: Start by showing that the integral is finite.

Definition 2.1.4. ($C^1$ curve in $\C $.) A curve $\gamma :[a,b]\to \C $ is a $C^1$ curve (in $\C $) if $(\re \gamma ,\im \gamma )$ is a $C^1$ curve (in $\R ^2$). We write

\begin{equation*}\gamma '(t)=\frac {d\gamma }{dt}=\frac {d(\re \gamma )}{dt}+i\frac {d(\im \gamma )}{dt}.\end{equation*}

(Problem 940) If $t\in (a,b)$ and $\gamma :[a,b]\to \C $ is $C^1$, show that $\gamma '(t)=\lim _{s\to t}\frac {\gamma (s)-\gamma (t)}{s-t}$.

Definition 2.1.5. (Complex line integral.) Let $\gamma \in C^1([a,b])$, $\gamma :[a,b]\to \Omega $ for some open set $\Omega \subseteq \C $ and $F:\Omega \to \C $ be continuous on $\Omega $. We define

\begin{equation*}\oint _\gamma F(z)\,dz=\int _a^b F(\gamma (t))\,\gamma '(t)\,dt\end{equation*}

(Problem 941) Let $ \gamma :[0,1]\to \Omega \subset \R ^2$ be a $C^1$ curve and let $\vec F:\Omega \to \R ^2$ be a vector-valued function. Recall that we identify $\R ^2$ with $\C $, so that we identify $ \gamma =(\gamma _1,\gamma _2)$ with $\gamma _1+i\gamma _2$ and $\vec F=(F_1,F_2)$ with $F=F_1+iF_2$.

\begin{equation*}\int _\gamma \vec F\cdot \tau \,ds = \re \oint _\gamma \overline {F}(z)\,dz, \qquad \int _\gamma \vec F\cdot \nu \,ds = \im \oint _\gamma \overline {F}(z)\,dz, \end{equation*}

where $\nu =\begin {pmatrix}0&1\\-1&0\end {pmatrix}\tau $ is the unit rightward normal vector to $\gamma $.

Proposition 2.1.6. Let $\gamma :[a,b]\to \Omega \subseteq \C $ be $C^1$, where $\Omega $ is open, and let $f$ be holomorphic in $\Omega $. Show that

\begin{equation*}\oint _\gamma \frac {\partial f}{\partial z}\,dz=f(\gamma (b))-f(\gamma (a)).\end{equation*}

(Problem 960) Prove Proposition 2.1.6. Hint: Start by computing $(f\circ \gamma )'(t)$ and the integrand in the definition of $\oint _\gamma \frac {\partial f}{\partial z}\,dz$.

Proposition 2.1.8. If $\gamma :[a,b]\to \Omega \subseteq \C $ is a $C^1$ curve and $f:\Omega \to \C $ is continuous, then $\displaystyle \left |\oint _\gamma f(z)\,dz\right |\leq \sup _{[a,b]} |f\circ \gamma | \cdot \ell (\gamma )=\sup _{\widetilde \gamma } |f| \cdot \ell (\gamma )$, where $\ell (\gamma )=\int _a^b |\gamma '|$.

Proposition 2.1.9. Let $\Omega \subseteq \C $ be open, let $F:\Omega \to \C $ be continuous, let $\gamma _1:[a,b]\to \Omega $ be a $C^1$ curve, and let $\varphi :[c,d]\to [a,b]$ be $C^1$ and satisfy $\varphi (c)=a$, $\varphi (d)=b$. Define $\gamma _2=\gamma _1\circ \varphi $. Then $\oint _{\gamma _1} F(z)\,dz=\oint _{\gamma _2} F(z)\,dz$.

(Problem 980) In this problem we begin the proof of Proposition 2.1.9. If $\varphi :[c,d]\to [a,b]$ is $C^1$ and $\gamma _1:[a,b]\to \C $ is $C^1$, show that $\gamma _2'(t) =\gamma _1'(\varphi (t))\,\varphi '(t)$ where $\gamma _2=\gamma _1\circ \varphi $.

(Problem 990) Let $\gamma _1:[a,b]\to \C $ be a $C^1$ curve. Let $\varphi :[c,d]\to [a,b]$ be continuous and satisfy $\varphi (c)=a$, $\varphi (d)=b$. Define $\gamma _2=\gamma _1\circ \varphi $. Compute $\gamma _2'(t)$ in terms of $\gamma _1$, $\gamma _1'$, $\varphi $, and $\varphi '$. Then show that $\widetilde \gamma _1=\widetilde \gamma _2$. (Recall $\widetilde \gamma $ denotes the image of $\gamma $.)

(Problem 1010) Let $\gamma _1:[-a,a]\to \C $. Let $\gamma _2:[-a,a]\to \C $ be given by $\gamma _2(t)=\gamma _1(-t)$. Show that if $F$ is continuous in a neighborhood of $\widetilde \gamma _1$, then $\oint _{\gamma _1} F(z)\,dz=-\oint _{\gamma _2} F(z)\,dz$.

(Problem 1020) Let $\gamma _1:[a,b]\to \C $ and $\gamma _2:[c,d]\to \C $ be two curves. Suppose further that $\widetilde \gamma _1=\widetilde \gamma _2$, $\gamma _1(a)=\gamma _2(c)$, $\gamma _1(b)=\gamma _2(d)$, and that $\gamma _1$ and $\gamma _2$ are injective. Show that there is a continuous strictly increasing function $\varphi :[c,d]\to [a,b]$ such that $\gamma _2=\gamma _1\circ \varphi $.

(Problem 1030) If $\gamma _1:[a,b]\to \C $ and $\gamma _2:[c,d]\to \C $ are simple closed curves rather than injective functions, with $\widetilde \gamma _1=\widetilde \gamma _2$ and $\gamma _1(a)=\gamma _1(b)=\gamma _2(c)=\gamma _2(d)$, is it necessarily the case that $\gamma _2=\gamma _1\circ \varphi $ for a continuous strictly increasing function $\varphi :[c,d]\to [a,b]$?

(Bonus Problem 1040) Let $\gamma _1:[a,b]\to \C $ and $\gamma _2:[c,d]\to \C $ be two curves. Suppose further that $\widetilde \gamma _1=\widetilde \gamma _2$, $\gamma _1(a)=\gamma _2(c)$, $\gamma _1(b)=\gamma _2(d)$, and that $\gamma _1$ and $\gamma _2$ are injective. Show that if $F$ is continuous in a neighborhood of $\widetilde \gamma _1$, then $\oint _{\gamma _1} F(z)\,dz=\oint _{\gamma _2} F(z)\,dz$. (This does not follow immediately from Problems 1000 and 1020 because $\varphi $ may not be continuously differentiable.)

(Problem 1050) Let $\gamma _1:[a,b]\to \C $ and $\gamma _2:[c,d]\to \C $ be two $C^1$ curves. Suppose that $\gamma _1(b)=\gamma _2(c)$. Show that there is a $C^1$ curve $\gamma _3:[-1,1]\to \C $ such that $\gamma _3\big \vert _{[-1,0]}$ is a reparameterization of $\gamma _1$ and $\gamma _3\big \vert _{[0,1]}$ is a reparameterization of $\gamma _2$. (We will write $\gamma _3=\gamma _1*\gamma _2$. This means that $\widetilde \gamma _3=\widetilde \gamma _1\cup \widetilde \gamma _2$ and $\oint _{\gamma _3} F(z)\,dz=\oint _{\gamma _1} F(z)\,dz+\oint _{\gamma _2} F(z)\,dz$ for all $F$ continuous in a neighborhood of $\widetilde \gamma _3$.)

2.2. Real Analysis

[Definition: Limit in metric spaces] If $(X,d)$ and $(Z,\rho )$ are metric spaces, $p\in Z$, and $f:Z\setminus \{p\}\to X$, we say that $\lim _{z\to p}f(z)=\ell $ if, for all $\varepsilon >0$, there is a $\delta >0$ such that if $z\in Z$ and $0<\rho (z,p)<\delta $, then $d(f(z),f(p))<\varepsilon $.

[Definition: Continuous function on metric spaces] If $(X,d)$ and $(Z,\rho )$ are metric spaces and $f:Z\to X$, we say that $f$ is continuous at $p\in Z$ if $f(p)=\lim _{z\to p} f(z)$.

(Fact 1060) Let $\Omega \subseteq \R ^2$ be open and let $f:\Omega \to \R $ be $C^1$. Let $\vec p\in \Omega $ and let $\vec \eta \in \R ^2$. Define $g(t)$ by $g(t)=f(\vec p+t\vec \eta )$. Suppose that $(\vec p+t\vec \eta )\in \Omega $. Then $g'(t)=\vec \eta \cdot \nabla f(\vec p+t\vec \eta )$.

(Problem 1070) Suppose that $\overline B(\vec p,\|\vec \eta \|)\subseteq \Omega $. Show that $f(\vec p+\vec \eta )-f(\vec p)=\vec \eta \cdot \nabla f(\vec w)$ for some $\vec w\in B(\vec p,r)$.

(Fact 1080) Let $\Omega \subseteq \R ^d$ be open and let $\vec f:\Omega \to \R ^n$ be $C^1$ (that is, the $n$ components $f_1$, $f_2,\dots ,f_n$ of $\vec f$ are all $C^1$). Let $\vec p\in \Omega $. Define $L:\R ^d\to \R ^n$ by

\begin{equation*}L(a_1,\dots ,a_d)=\sum _{k=1}^d \frac {\partial \vec f}{\partial x_k}\Big \vert _{\vec x=\vec p} a_k. \end{equation*}

Then $\lim _{\vec x\to \vec p} \frac {\|f(\vec x)-f(\vec p)-L(\vec x-\vec p)\|}{\|\vec x-\vec p\|}=0$. We often write $L=D\vec f(\vec p)$.

(Bonus Problem 1090) State and prove the chain rule for this form of derivative.

2.2. Complex Differentiability and Conformality

(Problem 1100) Let $\gamma :[0,1]\to \C $ be a parameterization of a nondegenerate scalene triangle of your choice. Sketch the trace of $\gamma $ and of $f\circ \gamma $ for the following choices of $f$:

[Definition: Complex derivative] Let $p\in \Omega \subseteq \C $, where $\Omega $ is open. Let $f:\Omega \to \C $. Suppose that $\lim _{z\to p} \frac {f(z)-f(p)}{z-p}$ exists. Then we say that $f$ has a complex derivative at $p$ and write $f'(p)=\lim _{z\to p} \frac {f(z)-f(p)}{z-p}$.

(Fact 1120) If $\Omega \subseteq \C $ is open, $p\in \Omega $, and $f$, $g:\Omega \setminus \{p\}\to \C $ are such that $\lim _{z\to p} f(z)$ and $\lim _{z\to p} g(z)$ exist (as complex numbers), then we have the usual formulas

\begin{gather*}\lim _{z\to p} \bigl (f(z)+g(z)\bigr )=\bigl (\lim _{z\to p} f(z)\bigr ) +\bigl (\lim _{z\to p} g(z)\bigr ), \\ \lim _{z\to p} \bigl (f(z)-g(z)\bigr )=\bigl (\lim _{z\to p} f(z)\bigr )-\bigl (\lim _{z\to p} g(z)\bigr ), \\ \lim _{z\to p} \bigl (f(z)g(z)\bigr )=\bigl (\lim _{z\to p} f(z)\bigr )\bigl (\lim _{z\to p} g(z)\bigr ) \end{gather*}

\begin{equation*}\lim _{z\to p} \frac {f(z)}{g(z)}=\frac {\lim _{z\to p} f(z)}{\lim _{z\to p} g(z)}.\end{equation*}

(Fact 1130) If $\Omega \subseteq \C $ and $W\subseteq \C $ are open, $p\in \Omega $, $f:\Omega \setminus \{p\}\to W$ is such that $L=\lim _{z\to p} f(z)$ exists, $L\in W$, and $g:W\to \C $ is continuous at $L$, then

\begin{equation*}\lim _{z\to p} g(f(z))=g(L).\end{equation*}

[Chapter 2, Problem 8] If $f'(p)$ exists, show that $\frac {\partial f}{\partial x}\big \vert _{x+iy=p}= \frac {1}{i}\frac {\partial f}{\partial y}\big \vert _{x+iy=p}= \frac {\partial f}{\partial z}\big \vert _{z=p} = f'(p)$.

[Chapter 2, Problem 10] If $f$ has a complex derivative at $p$, then $f$ is continuous at $p$.

(Problem 1140) (Note: If you are presenting this problem, do either part (a) or part (b), at your option. If you are citing this problem, you may use either part.)

Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be continuous.

Theorem 2.2.2. Suppose that $f$ has a complex derivative at $p$. Then $\frac {\partial f}{\partial z}\big \vert _{z=p}=f'(p)$.

(Problem 1150) Suppose that $f$ has a complex derivative at $p$. Prove Theorem 2.2.2 and also show that $\frac {\partial f}{\partial \overline z}\big \vert _{z=p}=0$. Hint: Start by writing the $\varepsilon $-$\delta $ definition of a limit of a function from $\Omega \setminus \{p\}$ to $\C $, where $p\in \Omega \subseteq \C $.

[Definition: Disc] The open disc (or ball) in $\C $ of radius $r$ and center $p$ is $D(p,r)=B(p,r)=\{z\in \C :|z-p|<r\}$. The closed disc (or ball) in $\C $ of radius $r$ and center $p$ is $\overline D(p,r)=\overline B(p,r)=\{z\in \C :|z-p|\leq r\}$.

Theorem 2.2.1. (Generalization.) Suppose that $\Omega \subseteq \C $ is open and that $f$ is $C^1$ on $\Omega $. Let $p\in \Omega $ and suppose $\p [f]{\bar z}\big \vert _{z=p}=0$. Then $f$ has a complex derivative at $p$ and $f'(p)=\frac {\partial f}{\partial z}\big \vert _{z=p}$.

(Problem 1170) Let $F:\R ^2\to \R ^2$. Suppose that $\nabla F_1$ and $\nabla F_2$ are constants. Show that $F(x,y)=F(0,0)+(\partial _1 F_1,\partial _1 F_2)x+(\partial _2 F_1,\partial _2 F_2)y$ for all $(x,y)\in \R ^2$.

(Problem 1180) Suppose that $f:\C \to \C $. Suppose that $f'$ exists everywhere and is a constant. Show that $f(z)=f(0)+f'(0)z$ for all $z\in \C $. Conclude that if $z$, $\omega $, $w\in \C $ with $\omega \neq z\neq w$, then $\frac {|f(\omega )-f(z)|}{|\omega -z|}=\frac {|f(w)-f(z)|}{|w-z|}$.

(Problem 1190) Let $F:\R ^2\to \R ^2$. Suppose that $\nabla F_1$ and $\nabla F_2$ are constants. If $C$ is a circle, what is $F(C)$? If $S$ is a square, what is $F(S)$? Now suppose that $f:\C \to \C $ and that $f'$ exists everywhere and is a constant. If $C$ is a circle, what is $f(C)$? If $S$ is a square, what is $f(S)$?

Theorem 2.2.3.1. Let $z_0\in \Omega \subseteq \C $ for some open set $\Omega $. Let $f:\Omega \to \C $. Let $w_1$, $w_2\in \C $ with $w_1$, $w_2\neq 0$. Suppose that $f'(z_0)$ exists. Then $\lim _{t\to 0} \frac {|f(z_0+tw_1)-f(z_0)|}{|tw_1|}=\lim _{t\to 0} \frac {|f(z_0+tw_2)-f(z_0)|}{|tw_2|}$.

(Problem 1200) Prove Theorem 2.2.3.1. How does this relate to the result of Problem 1180?

[Chapter 2, Problem 12] Let $z_0\in \Omega \subseteq \C $ for some open set $\Omega $. Let $f:\Omega \to \C $. Suppose that $\lim _{t\to 0} \frac {|f(z_0+tw_1)-f(z_0)|}{|tw_1|}=\lim _{t\to 0} \frac {|f(z_0+tw_2)-f(z_0)|}{|tw_2|}$ for all $w_1$, $w_2\in \C \setminus \{0\}$. Then either $f'(z_0)$ exists or $(\overline f)'(z_0)$ exists.

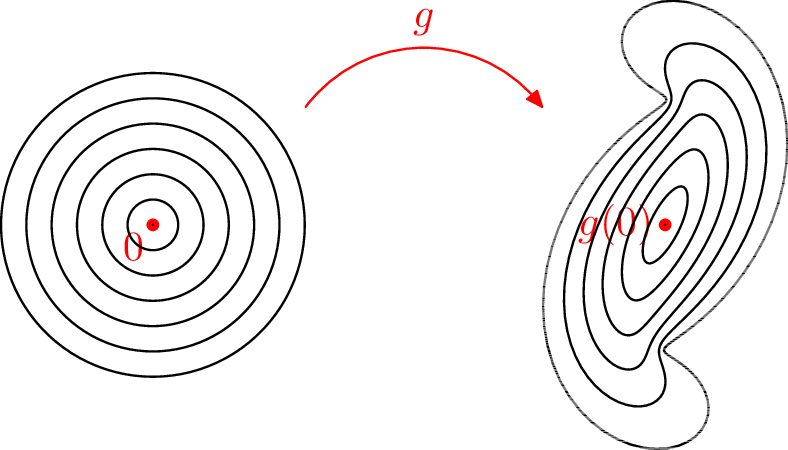
[Definition: Angle preserving] Let $z_0\in \Omega \subseteq \C $ for some open set $\Omega $. Let $f:\Omega \to \C $. We say that $f$ preserves angles at $z_0$ if, for all $w_1$, $w_2\in \C \setminus \{0\}$, we have that

\begin{equation*}\lim _{t\to 0^+} \frac {f(z_0+tw_1)-f(z_0)}{f(z_0+tw_2)-f(z_0)} \left | \frac {f(z_0+tw_2)-f(z_0)}{f(z_0+tw_1)-f(z_0)}\right | =\frac {w_1/|w_1|}{w_2/|w_2|}. \end{equation*}

and in particular that the denominators $f(z_0+tw_1)-f(z_0)$ and $f(z_0+tw_2)-f(z_0)$ are not zero when $t$ is sufficiently close to $0$. [This is not the definition in the book.]

Theorem 2.2.3.2. If $f'(z_0)$ exists and is not zero, then $f$ preserves angles at $z_0$.

[Chapter 2, Problem 9a] If $f$ is $C^1$ and preserves angles at $z_0$, then $f'(z_0)$ exists.

(Problem 1220) Consider the following figures. On the left is shown the traces of $\gamma _j$ for several values of $j$. On the right is shown the traces of $f\circ \gamma _j$, $g\circ \gamma _j$, or $h\circ \gamma _j$ for the same $\gamma _j$. You are given that exactly two of the quantities $f'(0)$, $g'(0)$, and $h'(0)$ exist and that exactly one of those quantities is zero. Based on the images, which function do you think has nonzero derivative, which has zero derivative, and which does not have a derivative?

2.3. Real Analysis

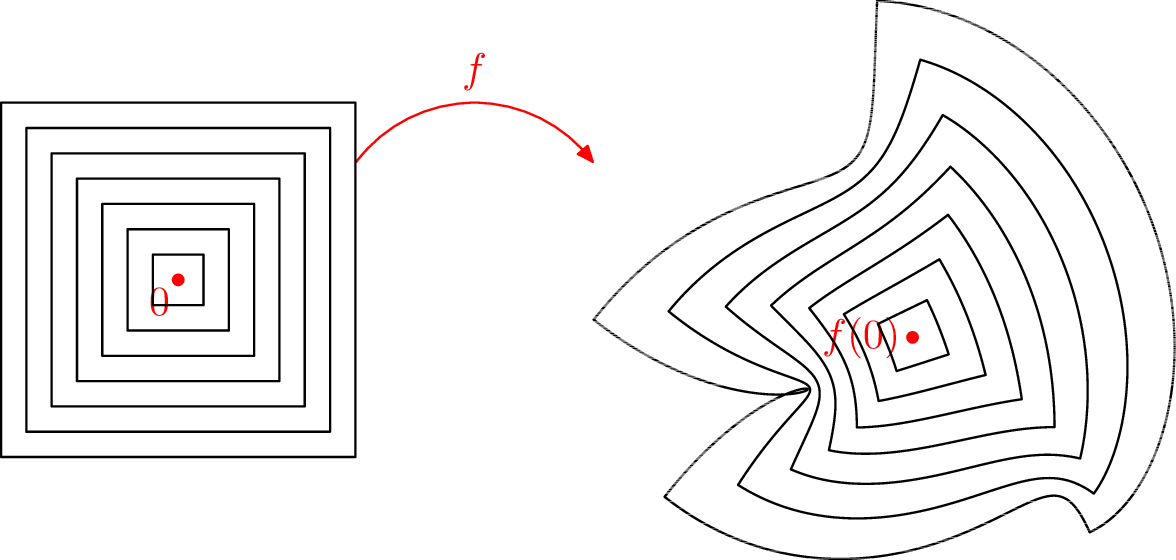
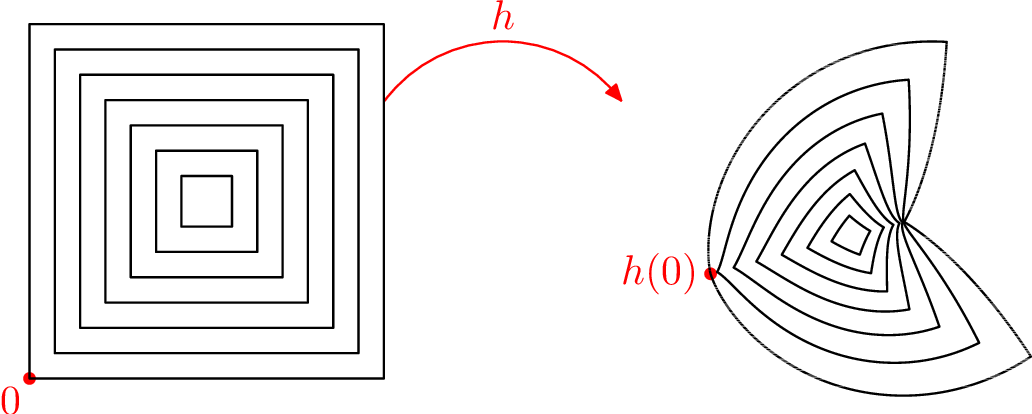
(Memory 1221) Let $f(x)=x^2\sin (1/x)$ if $x\neq 0$ and let $f(0)=0$. Then $f$ is continuous on $(-\infty ,\infty )$, continuously differentiable on $(-\infty ,0)$ and $(0,\infty )$, and $f'(0)$ exists, but the limit $\lim _{x\to 0} f'(x)$ does not exist.

Lemma 2.3.1. Suppose that $a<p<b$ and let $H:(a,b)\to \R $ be continuous. Suppose that $H$ is differentiable on both $(a,p)$ and $(p,b)$, and that $\lim _{x\to p} H'(x)=h$ for some $h\in \R $. Then $H'(p)$ exists and $H'(p)=\lim _{x\to p} H'(x)$.

2.3. Antiderivatives Revisited

(Memory 1230) Recall Problem 750: Suppose that there are two $C^1$ functions $g$ and $h$ defined in an open rectangle or disc $\mathcal {R}$ such that $\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h$. Then there is a function $f\in C^2(\mathcal {R})$ such that $\frac {\partial f}{\partial y}=g$ and $ \frac {\partial f}{\partial x}=h$.

Theorem 2.3.2. Let $\mathcal {R}\subset \R ^2$ be an open rectangle or disc and let $P\in \mathcal {R}$. Suppose that there are two functions $g$ and $h$ that are continuous on $\mathcal {R}$, continuously differentiable on $\mathcal {R}\setminus \{P\}$, and such that $\frac {\partial }{\partial x}g=\frac {\partial }{\partial y}h$ on $\mathcal {R}\setminus \{P\}$ for some $P\in \mathcal {R}$. Then there is a function $f\in C^1(\mathcal {R})$ such that $\frac {\partial f}{\partial y}=g$ and $ \frac {\partial f}{\partial x}=h$ everywhere in $\mathcal {R}$ (including at $P$).

Theorem 2.3.3. Let $P\in \mathcal {R}$, where $\mathcal {R}$ is an open rectangle or disc. Suppose that $f$ is continuous on $\mathcal {R}$ and holomorphic on $\mathcal {R}\setminus \{P\}$. Then there is a function $F$ that is holomorphic on all of $\mathcal {R}$ (including $P$) such that $\frac {\partial F}{\partial z} = f$.

(Problem 1260) Is the previous problem true if we relax the assumption that $f$ is continuous at $P$ (and that $\p [F]{z}=f$ at $P$)?

2.4. Real Analysis

(Memory 1280) In $\C $, $\partial D(P,r)=\partial \overline D(P,r)=\{z\in \C :|z-P|=r\}$.

2.4. The Cauchy Integral Formula and the Cauchy Integral Theorem

Theorem 2.4.3. [The Cauchy integral theorem.] Let $f$ be holomorphic in $D(P,R)$. Let $\gamma :[a,b]\to D(P,R)$ be a closed curve. Then $\oint _\gamma f(z)\,dz=0$.

Theorem 2.4.2. [The Cauchy integral formula.] Let $\Omega \subseteq \C $ be open and let $\overline D(z_0,r)\subset \Omega $. Let $f$ be holomorphic in $\Omega $ and let $z\in D(z_0,r)$. Then

\begin{equation*}f(z)=\frac {1}{2\pi i}\oint _\gamma \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}

Lemma 2.4.1. The Cauchy integral formula is true in the special case where $f(\zeta )=1$ for all $\zeta \in \C $.

(Problem 1281) Let $\gamma :[a,b]\to K$ be a $C^1$ curve for some set $K\subseteq \C $ (not necessarily open). Let $V\subseteq \C $ be compact and let $f: K\times V\to \C $ be continuous. Let $F:V\to \C $ be defined by

\begin{gather*} F(z)=\oint _\gamma f(\zeta ,z)\,d\zeta . \end{gather*}

(Problem 1290) In this problem we will begin the proof of Lemma 2.4.1 (and thus ultimately of Theorem 2.4.2). Let $\gamma :[a,b]\to K$ be a $C^1$ curve for some set $K\subseteq \C $ (not necessarily open). Let $W\subseteq \C $ be open and let $f: K\times W\to \C $ be continuous. Suppose that the functions $\frac {\partial f}{\partial x}$ and $\frac {\partial f}{\partial y}$ given by $\frac {\partial f}{\partial x}(\zeta ,x+iy)=\frac {\partial }{\partial x} f(\zeta ,x+iy)$ and $\frac {\partial f}{\partial y}(\zeta ,x+iy)=\frac {\partial }{\partial y} f(\zeta ,x+iy)$ are continuous on $K\times W$. Show that

\begin{gather*} \frac {\partial }{\partial x} \oint _\gamma f(\zeta ,x+iy)\,d\zeta = \oint _\gamma \frac {\partial }{\partial x} f(\zeta ,x+iy)\,d\zeta ,\\ \frac {\partial }{\partial y} \oint _\gamma f(\zeta ,x+iy)\,d\zeta = \oint _\gamma \frac {\partial }{\partial y} f(\zeta ,x+iy)\,d\zeta . ,\\ \frac {\partial }{\partial z} \oint _\gamma f(\zeta ,z)\,d\zeta = \oint _\gamma \frac {\partial }{\partial z} f(\zeta ,z)\,d\zeta . ,\\ \frac {\partial }{\partial \bar z} \oint _\gamma f(\zeta ,z)\,d\zeta = \oint _\gamma \frac {\partial }{\partial \bar z} f(\zeta ,z)\,d\zeta \end{gather*}

(Problem 1300) Prove Lemma 2.4.1. Hint: Start by proving Lemma 2.4.1 in the special case $z=z_0$. Computing $\re \oint _\gamma \frac {1}{\zeta -z}\,d\zeta $ and $\im \oint _\gamma \frac {1}{\zeta -z}\,d\zeta $ directly from the definition of line integral is very difficult if $z\neq z_0$. Instead compute $\frac {\partial }{\partial z} \oint _\gamma \frac {1}{\zeta -z}\,d\zeta $ and $\frac {\partial }{\partial \overline z} \oint _\gamma \frac {1}{\zeta -z}\,d\zeta $ and use the known value of $\oint _\gamma \frac {1}{\zeta -z_0}\,d\zeta $.

2.5. The Cauchy Integral Formula: Some Examples

(Problem 1310) Let $\gamma (t)=z_0+re^{i t}$, $0\leq t\leq 2\pi $. Let $n$ be an integer. Let $z\in D(z_0,r)$. Show that $\oint _\gamma (\zeta -z)^n\,d\zeta =0$ if $n\neq -1$.

(Problem 1320) Show that if $n\geq 0$ and $\gamma $ is as in the previous problem, then

\begin{equation*}\frac {1}{2\pi i}\oint _\gamma \frac {\zeta ^n}{\zeta -z}\,d\zeta =z^n.\end{equation*}

(As we have not yet proven the Cauchy integral formula, do not cite the Cauchy integral formula to perform this computation.)

(Problem 1330) Let $p\in \C [z]$ be a polynomial. Find $\frac {1}{2\pi i}\oint _\gamma \frac {p(\zeta )}{\zeta -z}\,d\zeta $. (As we have not yet proven the Cauchy integral formula, do not cite the Cauchy integral formula to perform this computation.)

2.4. The Cauchy Integral Formula and the Cauchy Integral Theorem

\begin{equation*}f(z)=\frac {1}{2\pi i}\oint _\gamma \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}

(Problem 1340) Prove Theorem 2.4.2. Hint: Let $h(\zeta )=\frac {f(\zeta )-f(z)}{\zeta -z}$ if $\zeta \neq z$. How should you define $h(z)$? What can you say about the behavior of $h$ at $z$ and in $\Omega \setminus \{z\}$?

[Definition: Integral over a circle] We define $\oint _{\partial D(P,r)} f(z)\,dz=\oint _\gamma f(z)\,dz$, where $\gamma $ is a counterclockwise simple parameterization of $\partial D(P,r)$.

[Chapter 2, Problem 20] Let $f$ be continuous on $\overline D(P,r)$ and holomorphic in $D(P,r)$. Show that $f(z)=\oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta $ for all $z\in D(P,r)$.

(Problem 1360) Let $f$ and $g$ be holomorphic in $D(P,r)$ and continuous on $\overline D(P,r)$. Suppose that $f(\zeta )=g(\zeta )$ for all $\zeta \in \partial D(P,r)$. Show that $f(z)=g(z)$ for all $z\in D(P,r)$.

Coda: Change of variables

(Problem 1370) Let $\Omega \subseteq \C $ be open, let $\gamma :[0,1]\to \Omega $ be a $C^1$ curve, and let $u:\Omega \to \C $ be holomorphic. Show that $u\circ \gamma $ is also a $C^1$ curve and that $(u\circ \gamma )'(t)=u'(\gamma (t))\,\gamma '(t)$.

(Problem 1380) Let $\Omega $, $W\subseteq \C $ be open and let $u:\Omega \to W$ be holomorphic. Let $\gamma :[0,1]\to \Omega $ be a $C^1$ closed curve. Let $f:W\to \C $ be continuous. Show that

\begin{equation*}\oint _{u\circ \gamma } f(w)\,dw = \oint _\gamma f(u(z))\,\frac {du}{dz}\,dz.\end{equation*}

(Problem 1390) I want to compute $\int _{-1}^1 \frac {(t+i)^3}{(t+i)^4+1}dt$. A naïve student uses the $u$-substitution $u=(t+i)^4$ and converts the integral to $\int _{-4}^{-4} \frac {1}{4} \frac {1}{u+1} du=0$. But when I compute $\int _{-1}^1 \frac {(t+i)^3}{(t+i)^4+1}dt$ using a numerical solver, I get $-i\pi /2$. What went wrong?

2.6. An Introduction to the Cauchy Integral Theorem and the Cauchy Integral Formula for More General Curves

Proposition 2.6.6. Let $\Omega =D(P,\tau )\setminus \overline D(P,\sigma )$ for some $P\in \C $ and some $0<\sigma <\tau $. Let $\sigma <r<R<\tau $ and let $\gamma _r$, $\gamma _R$ be the counterclockwise parameterizations of $\partial D(P,r)$, $\partial D(P,R)$. Suppose that $f$ is holomorphic in $\Omega $. Then $\oint _{\gamma _r} f=\oint _{\gamma _R} f$.

(Problem 1400) Prove Proposition 2.6.6. Hint: Define $\gamma _s$ in the natural way and find a function $h$ such that $\frac {d}{ds}\oint _{\gamma _s} f=\oint _{\gamma _s} h$.

[Definition: Homotopic curves] Let $a<b$, $c<d$. Let $\Omega \subseteq \C $ be open. Let $\gamma _c$, $\gamma _d:[a,b]\to \Omega $ be two $C^1$ curves with the same endpoints (so $\gamma _c(a)=\gamma _d(a)$, $\gamma _c(b)=\gamma _d(b)$).

We say that $\gamma _c$ and $\gamma _d$ are $C^1$-homotopic in $\Omega $ if there is a function $\Gamma $ such that:

[Definition: Homotopic closed curves] Let $a<b$, $c<d$. Let $\Omega \subseteq \C $ be open. Let $\gamma _c$, $\gamma _d:[a,b]\to \Omega $ be two closed $C^1$ curves.

We say that $\gamma _c$ and $\gamma _d$ are $C^1$-homotopic in $\Omega $ if there is a function $\Gamma $ such that:

(Bonus Problem 1401) Show that the assumption that $\Gamma $ be $C^1$ in the first variable is unnecessary: if $\gamma _c$ and $\gamma _d$ are $C^1$ and there is a function $\Gamma $ satisfying all of the above conditions except that $\Gamma $ is not $C^1$ in the first variable, then $\Gamma $ may be perturbed slightly to yield a $C^1$ function.

(Problem 1410) Let $\Omega =D(P,\tau )\setminus \overline D(P,\sigma )$ for some $P\in \C $ and some $0<\sigma <\tau $. Let $\sigma <r<R<\tau $ and let $\gamma _r$, $\gamma _R$ be the counterclockwise parameterizations of $\partial D(P,r)$, $\partial D(P,R)$. Show that $\gamma _r$ and $\gamma _R$ are homotopic in $\Omega $.

(Problem 1420) Let $\Omega $ be an open set, and let $\gamma _c$, $\gamma _d:[a,b]\to \Omega $ be two curves with the same endpoints that are homotopic in $\Omega $. Let $\Gamma $ be the homotopy.

Suppose that $\nabla \Gamma $ exists and is continuous on $[a,b]\times [c,d]$ (with the derivatives on the boundary defined as one-sided limits, as in Problem 890). Suppose further that $\nabla \Gamma $ is continuously differentiable on $[a,b]\times [c,d]$.

Let $\gamma _s(t)=\Gamma (t,s)$. Let $f$ be holomorphic on $\Omega $. Show that $\oint _{\gamma _c} f=\oint _{\gamma _d}f$. Hint: Start by computing $\frac {d}{ds}\oint _{\gamma _s} f$ and then rewrite the result as as $\int _a^b \p {t} h(s,t)\,dt$ for some function $h$.

(Bonus Problem 1430) Let $\Omega \subseteq \C $ be an open set, let $\gamma _c$ and $\gamma _d$ be two curves homotopic in $\Omega $ with the same endpoints, and let $f:\Omega \to \C $ be holomorphic. Show that $\oint _{\gamma _c} f=\oint _{\gamma _d}f$ even if the homotopy is merely continuous and $C^1$ in the first variable.

(Problem 1440) Let $\Omega \subseteq \C $ be any open set, let $\gamma _c$ and $\gamma _d$ be any two closed curves that are homotopic in $\Omega $, and let $f:\Omega \to \C $ be holomorphic. Assume the homotopy is $C^2$. Show that $\oint _{\gamma _c} f=\oint _{\gamma _d}f$. Hint: Start by computing $\frac {d}{ds}\oint _{\gamma _s} f$ and then rewrite the result as as $\int _a^b \p {t} h(s,t)\,dt$ for some function $h$.

(Problem 1450) Let $\Omega $ be open and let $f:\Omega \to \C $ be holomorphic.

3.1. Differentiability Properties of Holomorphic Functions

Theorem 3.1.3. [Generalization.] Let $D(P,r)\subset \C $. Let $\varphi :\partial D(P,r)\to \C $ be continuous. Let $k$ be a nonnegative integer. Define $f:D(P,r)\to \C $ by

\begin{equation*}f(z)=\frac {k!}{2\pi i} \oint _{\partial D(P,r)} \frac {\varphi (\zeta )}{(\zeta -z)^{k+1}}\,d\zeta .\end{equation*}

\begin{equation*}\p [f]{z}=\frac {(k+1)!}{2\pi i} \oint _{\partial D(P,r)} \frac {\varphi (\zeta )}{(\zeta -z)^{k+2}}\,d\zeta .\end{equation*}

(Problem 1460) Let $f$ be as in Theorem 3.1.3. Begin the proof of Theorem 3.1.3 by showing that $\p [f]{z}$ and $\p [f]{\bar z}$ exist and satisfy

\begin{equation*}\p [f]{z}=\frac {(k+1)!}{2\pi i} \oint _{\partial D(P,r)} \frac {\varphi (\zeta )}{(\zeta -z)^{k+2}}\,d\zeta , \qquad \p [f]{\bar z}=0. \end{equation*}

(Problem 1470) Complete the proof of Theorem 3.1.3 by showing that $f\in C^1(\Omega )$ and so is holomorphic.

[Chapter 2, Problem 21] If $z\in \partial D(P,r)$, is it necessarily true that $\lim _{w\to z} f(w)=\varphi (z)$?

Theorem 3.1.1. Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be holomorphic. Then $f\in C^\infty (\Omega )$. Moreover, if $\overline D(P,r)\subset \Omega $, then

\begin{equation*}\frac {\partial ^k f}{\partial z^k}(z) = \frac {k!}{2\pi i} \oint _{\partial D(P,r)} \frac {f(\zeta )}{(\zeta -z)^{k+1}}\,d\zeta .\end{equation*}

Corollary 3.1.2. Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be holomorphic. Then $\frac {\partial ^k f}{\partial z^k}$ is holomorphic in $\Omega $ for all $k\in \N $.

(Problem 1481) (Problem 1281) Let $\gamma :[a,b]\to K$ be a $C^1$ curve for some set $K\subseteq \C $ (not necessarily open). Let $V\subseteq \C $ be compact and let $f: K\times V\to \C $ be continuous. Let $F:V\to \C $ be defined by

\begin{gather*} F(z)=\oint _\gamma f(\zeta ,z)\,d\zeta . \end{gather*}

(Problem 1490) Suppose that $P\in \Omega \subseteq \C $ for some open set $\Omega $. Suppose that $f$ is continuous on $\Omega $ and holomorphic on $\Omega \setminus \{P\}$. Show that $f$ is holomorphic on $\Omega $.

Notes on Homework 5

[Chapter AB, Problem 5] The function $\log :\C \setminus (-\infty ,0]$ given by

if $z=|z|e^{i\theta }$ and $-\pi <\theta <\pi $ is holomorphic on $\C \setminus (-\infty ,0]$ and satisfies

(Problem 1491) Let $\Omega =\R ^2\setminus (-\infty ,0]$. Define a function $F:\Omega \to \R $ such that if $x+iy=re^{i\theta }$ for some real numbers $x$, $y$, $r$, $\theta $ with $r>0$ and $-\pi <\theta <\pi $, then we have that $F(x,y)=\theta $.

(Problem 1492) Let $W\subset \R ^2\setminus \{(0,0)\}$ be open. Let $\Omega =\{re^{i\theta }:(r,\theta )\in W\}$ and suppose that $\Omega $ is open. Let $F:\Omega \to \C $ be holomorphic. Define $f:W\to \C $ by $f(r,\theta )=F(re^{i\theta })$.

3.1. Real Analysis

(Memory 1500) Let $\Omega \subseteq \C $ be open and connected. Show that $\Omega $ is path connected and that the paths may be taken to be $C^1$; that is, if $z$, $w\in \Omega $ then there is a $\gamma :[0,1]\to \Omega $ with $\gamma $ a $C^1$ function such that $\gamma (0)=z$ and $\gamma (1)=w$.

3.1. Morera’s theorem

Theorem 3.1.4. (Morera’s theorem.) Let $\Omega \subseteq \C $ be open and connected. Let $f\in C(\Omega )$ be such that $\oint _\gamma f=0$ for all closed curves $\gamma $. Then $f$ is holomorphic in $\Omega $.

(Problem 1510) Prove Morera’s theorem. Furthermore, show that there is a function $F$ holomorphic in $\Omega $ such that $F'=f$.

(Problem 1520) Can you rewrite Morera’s theorem to involve a statement true for all holomorphic functions (can you write it with the phrase “if and only if”)?

3.2. Real Analysis

(Memory 1530) State the Root Test and Ratio Test from undergraduate real analysis.

[Definition: Taylor series] Let $f\in C^\infty (a,b)$ and let $a<c<b$. The Taylor series for $f$ at $c$ is $\sum _{n=0}^\infty \frac {f^{(n)}(c)}{n!}(x-c)^n$ (with the convention $0^0=1$).

(Memory 1540) Let $P_{m,c}(x)=\sum _{n=0}^m \frac {f^{(n)}(c)}{n!}(x-c)^n$ be the $m$th partial sum of the Taylor series at $c$. Suppose that $x\in (a,b)$, $x\neq c$, $m\in \N $. Show that there is a $y_{m}\in (a,b)$ with $|y_{m}-c|<|x-c|$ such that

\begin{equation*}f(x)=P_{m-1,c}(x)+\frac {1}{m!}f^{(m)}(y_m) \,(x-c)^{m}. \end{equation*}

(Memory 1550) The Taylor series for $\sin $, $\cos $, and $\exp $ converge to the parent function on all of $\R $.

(Problem 1560) Give an example of a function $f\in C^\infty (\R )$ such that the Taylor series for $f$ converges for all $x\in \R $ but such that $f(x)\neq \sum _{n=0}^\infty \frac {f^{(n)}(c)}{n!}(x-c)^n$ for all $x\neq c$.

(Problem 1570) Give an example of a function $f\in C^\infty (-2,\infty )$ such that the Taylor series for $f$ at $2$ diverges for all $|x-2|>2$. Can we do this for a function $f\in C^\infty (\R )$?

(Bonus Problem 1580) Give an example of a function $f\in C^\infty (\R )$ such that the Taylor series for $f$ at $0$ diverges for all $x\neq 0$.

[Definition: Absolute convergence] Let $\sum _{n=0}^\infty a_n$ be a series of real numbers. If $\sum _{n=0}^\infty |a_n|$ converges, then we say $\sum _{n=0}^\infty a_n$ converges absolutely.

[Definition: Uniform convergence] Let $E$ be a set, let $(X,d)$ be a metric space, and let $f_k$, $f:E\to X$. We say that $f_k\to f$ uniformly on $E$ if for every $\varepsilon >0$ there is a $N\in \N $ such that if $k\geq N$, then $d(f_k(z),f(z))<\varepsilon $ for all $z\in E$.

[Definition: Uniformly Cauchy] Let $E$ be a set, let $(X,d)$ be a metric space, and let $f_k:E\to X$. We say that $\{f_k\}_{k=1}^\infty $ is uniformly Cauchy on $E$ if for every $\varepsilon >0$ there is a $N\in \N $ such that if $n>m\geq N$, then $d(f_n(z),f-m(z))<\varepsilon $ for all $z\in E$.

[Definition: Uniform convergence and Cauchy for series] If $E$ is a set, $V$ is a vector space, and $f_k:E\to V$ for each $k\in \N $, then the series $\sum _{k=1}^\infty f_k$ converges uniformly to $f:E\to V$ or is uniformly Cauchy, respectively, if the sequences of partial sums $\bigl \{\sum _{k=1}^n f_k\bigr \}_{n=1}^\infty $ converge uniformly or are uniformly Cauchy.

(Memory 1590) Suppose that $(X,d)$ is a complete metric space. Then any uniformly Cauchy sequence is uniformly convergent.

(Memory 1600) Suppose that $(E,\rho )$ and $(X,d)$ are two metric spaces. Let $f_k$, $f:E\to X$. Suppose $f_k\to f$ uniformly on $E$ and that each $f_k$ is continuous. Then $f$ is also continuous.

(Problem 1601) Give an example of a compact metric space $(X,d)$ and a sequence of continuous functions from $X$ to $\R $ that converge pointwise, but not uniformly, to a continuous function.

(Memory 1610) Let $f_k$, $f:[a,b]\to \R $. Suppose that each $f_k$ is Riemann integrable and that $f_k\to f$ uniformly on $[a,b]$. Then $f$ is Riemann integrable, $\lim _{k\to \infty }\int _a^b f_k$ exists, and $\lim _{k\to \infty }\int _a^b f_k=\int _a^b f$.

(Memory 1611) (The Weierstrauß $M$-test.) Suppose that $A$ is a set and that for each $n$, $f_n:A\to \C $ is a bounded function. Suppose that there is a sequence $\{M_n\}_{n=0}^\infty \subset [0,\infty )$ such that $|f_n(x)|\leq M_n$ for all $x\in A$ and $\sum _{n=0}^\infty M_n<\infty $. Then the series $\sum _{n=0}^\infty f_n(x)$ converges absolutely and uniformly on $A$.

3.2. Complex Power Series

(Problem 1620) Let $\sum _{n=0}^\infty a_n$ be a series of complex numbers. Show that if $\sum _{n=0}^\infty |a_n|$ converges then $\sum _{n=0}^\infty a_n$ converges (that is, that in the complex numbers, we still have that absolute convergence implies convergence).

Definition 3.2.2. (Complex power series.) A complex power series is a formal sum $\sum _{k=0}^\infty a_k (z-P)^k$ for some $\{a_k\}_{k=1}^\infty \subseteq \C $. The series converges at $z$ if $\lim _{n\to \infty } \sum _{k=0}^n a_k (z-P)^k$ exists.

Lemma 3.2.3. Suppose that the series $\sum _{k=0}^\infty a_k (z-P)^k$ converges at $z=w$ for some $w\in \C $. Then the series converges absolutely at $z$ for all $z$ with $|z-P|<|w-P|$.

Proposition 3.2.9. Suppose that the series $\sum _{k=0}^\infty a_k (z-P)^k$ converges at $z=w$ for some $w\in \C $. If $0<r<|w-P|$, then the series converges uniformly on $\overline D(P,r)$.

(Problem 1650) Suppose that the series diverges at $w$ for some $w\in \C $. Show that the series diverges at $z$ for all $z$ with $|z-P|>|w-P|$.

Definition 3.2.4. (Radius of convergence.) The radius of convergence of $\sum _{k=0}^\infty a_k (z-P)^k$ is $\sup \{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k$ converges$\}$.

(Problem 1660) Show that the radius of convergence is also $\inf \{|w-P|:\sum _{k=0}^\infty a_k (w-P)^k$ diverges$\}$.

(Problem 1670) (Lemma 3.2.6.) State the root test from undergraduate real analysis. What does the root test say about complex power series?

(Problem 1680) State the ratio test from undergraduate real analysis. What does the ratio test say about power series?

Lemma 3.2.10. Let $\sum _{k=0}^\infty a_k (z-P)^k$ be a power series with radius of convergence $R>0$. Define $f:D(P,R)\to \C $ by $f(z)=\sum _{k=0}^\infty a_k (z-P)^k$.

Then $f$ is $C^\infty $ and holomorphic in $D(P,R)$, and if $n\in \N $ then the series

\begin{equation*}\sum _{k=n}^\infty \frac {k!}{(k-n)!}a_k (z-P)^{k-n}\end{equation*}

has radius of convergence at least $R$ and converges to $f^{(n)}(z)=\frac {\partial ^n f}{\partial z^n}$.

(Problem 1690) Begin the proof of Lemma 3.2.10 by showing that $f$ is continuous on $D(P,R)$.

(Problem 1700) Continue the proof of Lemma 3.2.10 by showing that $f$ is holomorphic in $D(P,R)$.

\begin{equation*}\sum _{k=n}^\infty \frac {k!}{(k-n)!}a_k (z-P)^{k-n}\end{equation*}

indeed converges to $f^{(n)}(z)$. Hint: Use Theorem 3.1.1 (Problem 1480) and Memory 1610.

[Definition: Taylor series] Let $P\in \Omega \subseteq \C $ where $\Omega $ is open, and let $f$ be holomorphic in $\Omega $. By Theorem 3.1.1 (Problem 1480), $f^{(n)}$ exists everywhere in $\Omega $. The Taylor series for $f$ at $P$ is the power series $\sum _{k=0}^\infty \frac {f^{(k)}(P)}{k!}(z-P)^k$.

(Problem 1720) Let $f$ be as in Lemma 3.2.10. Show that the Taylor series for $f$ at $P$ is simply $\sum _{k=0}^\infty a_k (z-P)^k$.

Proposition 3.2.11. Suppose that the two power series $\sum _{k=0}^\infty a_k (z-P)^k$ and $\sum _{k=0}^\infty b_k (z-P)^k$ both have positive radius of convergence and that there is some $r>0$ such that $\sum _{k=0}^\infty a_k (z-P)^k=\sum _{n=0}^\infty b_k (z-P)^k$ (and both sums converge) whenever $|z-P|<r$. Then $a_k=b_k$ for all $k$.

[Definition: Analytic function] Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be a function. If for every $P\in \Omega $ there is a $r>0$ with $D(P,r)\subseteq \Omega $ and a sequence $\{a_n\}_{n=1}^\infty \subset \C $ such that $f(z)=\sum _{n=0}^\infty a_n (z-P)^n$ for all $z\in D(P,r)$, we say that $f$ is analytic.

(Problem 1750) Recall that if $x\in \R $, then $\exp x=\sum _{n=0}^\infty \frac {x^n}{n!}$, $\sin x=\sum _{n=0}^\infty \frac {(-1)^n}{(2n+1)!}x^{2n+1}$, $\cos x=\sum _{n=0}^\infty \frac {(-1)^n}{(2n)!}x^{2n}$. Show that the functions $\exp z=\sum _{n=0}^\infty \frac {z^n}{n!}$, $\sin z=\sum _{n=0}^\infty \frac {(-1)^n}{(2n+1)!}z^{2n+1}$, and $\cos z=\sum _{n=0}^\infty \frac {(-1)^n}{(2n)!}z^{2n}$ are holomorphic on $\C $ and take the correct values at all real numbers.

3.3. The Power Series Expansion for a Holomorphic Function

Theorem 3.3.1. Let $\Omega \subseteq \C $ be an open set and let $f$ be holomorphic in $\Omega $. Let $D(P,r)\subseteq \Omega $ for some $r>0$.

Then the Taylor series for $f$ at $P$ has radius of convergence at least $r$ and converges to $f(z)$ for all $z\in D(P,r)$.

(Problem 1760) Let $f$ be holomorphic in $D(P,R)$ and let $0<r<R$. Begin the proof of Theorem 3.3.1 by showing that there is a power series with radius of convergence at least $r$ that converges to $f$ in $D(P,r)$.

(Problem 1770) Complete the proof of Theorem 3.3.1 by show that the power series for $f$ in $D(P,r)$ must be the Taylor series for $f$ at $P$ and that the radius of convergence of the Taylor series for $f$ at $P$ must be at least $R$.

(Problem 1780) Let $f$ be holomorphic in $D(P,r)$. Let $R$ be the radius of convergence of the Taylor series for $f$ at $P$. Observe that $R\geq r$. Suppose $R>r$. Show that there is a unique function $F$ that is holomorphic in $D(P,R)$ with $F=f$ in $D(P,r)$.

(Problem 1790) Let $f$ be an analytic function in a neighborhood of $P$. Show that the Taylor series for $f'$ at $P$ has the same radius of convergence as the Taylor series for $f$ at $P$.

(Problem 1800) Let $\Omega =\{re^{i\theta }:0<r<\infty ,\>-\pi <\theta <\pi \}=\C \setminus (-\infty ,0]$. Define $F:\Omega \to \C $ by $F(re^{i\theta })=\ln r+i\theta $ whenever $-\pi <\theta <\pi $. Recall that $F$ is holomorphic and that $F'(z)=\frac {1}{z}$ for all $z\in \Omega $.

(Fact 1801) Recall from Proposition 1.4.3 (Problem 660) that if $f$ is holomorphic in $\Omega $ then $\p [f]{z}=\p [f]{x}$ in $\Omega $. By Corollary 3.1.2 (Problem 1480), $\p [f]{z}=\p [f]{x}$ is holomorphic in $\Omega $. A straightforward induction argument yields that $\frac {\partial ^n f}{\partial z^n}=\frac {\partial ^n f}{\partial x^n}$ in $\Omega $ for all $n\in \N $.

(Problem 1810) Show that the functions $\exp $, $\sin $, and $\cos $ in Problem 1750 are the only functions that are holomorphic on all of $\C $ and take the correct values for all real numbers.

(Problem 1820) Suppose that $\sum _{n=0}^\infty a_n z^n$ and $\sum _{n=0}^\infty b_n z^n$ are two power series with radius of convergence at least $r$. Show that

\begin{equation*}\sum _{n=0}^\infty \Bigl (\sum _{k=0}^n a_k\, b_{n-k}\Bigr )z^n\end{equation*}

\begin{equation*}\sum _{n=0}^\infty \Bigl (\sum _{k=0}^n a_k\, b_{n-k}\Bigr )z^n = \biggl (\sum _{n=0}^\infty a_n z^n\biggr )\biggl (\sum _{n=0}^\infty b_n z^n\biggr )\end{equation*}

3.4. The Cauchy Estimates and Liouville’s Theorem

Theorem 3.4.1. (The Cauchy estimates) Let $f:\Omega \to \C $ be holomorphic and let $\overline D(P,r)\subseteq \Omega $. Let $k\in \N _0$. Then

\begin{equation*}\biggl |\frac {\partial ^k f}{\partial z^k}\Big \vert _{z=P}\biggr | \leq \frac {k!}{r^k} \sup _{z\in \partial D(P,r)}|f(z)|.\end{equation*}

(Problem 1840) Let $k$, $n\in \N $. Show that there is a function $f\in C^\infty (\R )$ with $\sup _{x\in \R } |f(x)|\leq 1$ but with $|f^{(k)}(0)|\geq n$.

Lemma 3.4.2. If $f$ is holomorphic on a connected open set $\Omega $ and $\p [f]{z}=0$ in $\Omega $, then $f$ is constant. (This was proven in Problem 590.)

(Problem 1850) Let $P\in \C $, $r>0$, $k\in \N $, and let $f:D(P,r)\to \C $ be holomorphic. Suppose that $\frac {\partial ^{k+1} f}{\partial z^{k+1}}=0$ in $D(P,r)$. Show that $f$ is a polynomial of degree at most $k$.

(Bonus Problem 1860) Show that this is still true in an arbitrary connected open set.

[Definition: Entire] A function $f:\C \to \C $ is entire if $f$ is holomorphic on all of $\C $.

[Exercise: Theorem 3.4.4]. If $f$ is entire and there is a constant $C\in \R $ and a $k\in \N _0$ such that $|f(z)|\leq C+C|z|^k$ for all $z\in \C $, then $f$ is a polynomial of degree at most $k$.

Theorem 3.4.5. (The fundamental theorem of algebra.) Let $p$ be a nonconstant (holomorphic) polynomial. Prove that $p$ has a root; that is, prove that there is an $\alpha \in \C $ with $p(\alpha )=0$.

[Chapter 3, Problem 36] Let $p(z)=a_0+a_1z+\dots +a_nz^n$ be a polynomial. Show that there is an $R\in (0,\infty )$ such that if $|z|\geq R$, then $|p(z)|\geq |a_n|\,|z|^n/2$.

(Problem 1890) (Corollary 3.4.6.) Let $p$ be a polynomial of degree $k>0$. Can $p$ necessarily be factored completely?

3.5. Uniform Limits of Holomorphic Functions

Theorem 3.5.1. Let $\Omega \subseteq \C $ be a domain. Let $f_j$, $f:\Omega \to \C $. Suppose that each $f_j$ is holomorphic in $\Omega $ and that if $K\subset \Omega $ is compact, then $f_j\to f$ uniformly on $K$. Then $f$ is holomorphic in $\Omega $.

(Problem 1910) Give an example of a sequence of functions in $C^\infty (\R )$ that converge uniformly to a function that is not differentiable.

Corollary 3.5.2. Let $\Omega \subseteq \C $ be a domain. Let $f_j$, $f:\Omega \to \C $. Suppose that each $f_j$ is holomorphic in $\Omega $ and that if $K\subset \Omega $ is compact, then $f_j\to f$ uniformly on $K$. Then $\frac {\partial }{\partial z} f_j\to \frac {\partial }{\partial z} f$ on $\Omega $ and the convergence is uniform on all compact subsets $X$ of $\Omega $.

(Problem 1930) Give an example of a sequence of functions $\{f_n\}_{n=1}^\infty $ in $C^\infty (\R )$ that converge uniformly to a differentiable function $f$ but where $f_n'$ does not converge to $f'$.

3.6. Real Analysis

(Problem 1940) Show that the real Taylor series for $f(x)=\ln x$ at any point $c\in (0,\infty )$ has a positive radius of convergence and converges to $\ln x$.

[Definition: Relatively open and closed] Let $(X,d)$ be a metric space and let $Y\subseteq X$. Then $(Y,d)$ is also a metric space. If $F\subseteq Y$ is closed in $(Y,d)$, then we say that $F$ is relatively closed. If $G\subseteq Y$ is open in $(Y,d)$, then we say that $G$ is relatively open.

(Memory 1950) Suppose that $F\subseteq X$ is closed. Then $F\cap Y$ is relatively closed in $Y$. In particular, if $F\subseteq Y$ and $F$ is closed in $(X,d)$, then $F$ is relatively closed in $(Y,d)$.

(Memory 1960) Suppose that $G\subseteq X$ is open. Then $G\cap Y$ is relatively open in $Y$.

(Problem 1970) Give an example of a metric space $(X,d)$, a subset $Y\subset X$, and a set $F\subseteq Y$ such that $F$ is relatively closed in $(Y,d)$ but not closed in $(X,d)$.

(Problem 1980) Give an example of a metric space $(X,d)$, a subset $Y\subset X$, and a set $G\subseteq Y$ such that $G$ is relatively open in $(Y,d)$ but not open in $(X,d)$.

3.6. The Zeros of a Holomorphic Function

Corollary 3.6.2. Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic. Suppose that there is a $P\in \Omega $ and an $r>0$ such that $D(P,r)\subseteq \Omega $ and $f=0$ in $D(P,r)$. Then $f=0$ everywhere in $\Omega $.

Corollary 3.6.5. Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic. Suppose that there is a $P\in \Omega $ such that $f^{(k)}(P)=0$ for all $k\in \N _0$ (that is, all integers $k$ such that $k\geq 0$). Then $f=0$ everywhere in $\Omega $.

(Problem 2010) In this problem we begin the proof of Corollaries 3.6.2 and 3.6.3. Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be holomorphic. Let

\begin{align*}E&=\{z\in \Omega :\text { there is a $r>0$ such that $D(z,r)\subseteq \Omega $ and $f=0$ in $D(z,r)$}\}, \\ F&=\{z\in \Omega :f^{(k)}(z)=0\text { for all }k\in \N _0\} .\end{align*}

(Problem 2020) $E$ is clearly open. Complete the proof of Corollaries 3.6.2 and 3.6.5 by showing that $F$ is relatively closed in $\Omega $ and then drawing appropriate conclusions if $\Omega $ is connected.

Theorem 3.6.1. Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic.

(Problem 2040) Give an example of a function $f$ holomorphic in $\C \setminus \{0\}$ and a sequence of points $z_n\in \C \setminus \{0\}$ with $z_n\to 0$ and with $f(z_n)=0$ but where $f(z)\neq 0$ for some $z\in \C \setminus \{0\}$.

[Definition: Accumulation point] Let $S\subseteq \C $. Suppose that $P\in \C $ and that, for every $r>0$, there is a $z\in D(P,r)\cap S$ with $z\neq P$. Then we say that $P$ is an accumulation point for $S$.

(Problem 2041) Rewrite Theorem 3.6.1 in terms of accumulation points rather than sequences and prove your version.

(Problem 2050) Let $\Omega $ be a connected open set and let $f:\Omega \to \C $ be holomorphic and not constant. Let $P\in \Omega $. Show that there is a $r>0$ with $D(P,r)\subseteq \Omega $ and such that $f\neq 0$ on $D(P,r)\setminus \{P\}$.

Corollary 3.6.3. Suppose that $f$ and $g$ are holomorphic in a connected open set $\Omega $. If $\{z\in \Omega :f(z)=g(z)\}$ has an accumulation point in $\Omega $, then $f(z)=g(z)$ for all $z\in \Omega $.

(Problem 2070) Let $\Omega \subseteq \C \setminus \{0\}$ be open and connected and contain a positive real. Show that there is at most one function $f:\Omega \to \C $ such that $f(x)=\ln x$ for all $x\in (0,\infty )\cap \Omega $.

Corollary 3.6.4. Suppose that $f$ and $g$ are holomorphic in a connected open set $\Omega $. If $fg=0$ everywhere in $\Omega $, then either $f\equiv 0$ or $g\equiv 0$ in $\Omega $.

[Chapter 3, Problem 42] Let $f$ be holomorphic in the connected open set $\Omega $ and let $K\subseteq \Omega $ be compact. Show that if $f$ has infinitely many zeroes in $K$ then $f\equiv 0$ in $\Omega $.

4.1. The Behavior of a Holomorphic Function Near an Isolated Singularity

[Definition: Isolated singularity] If $\Omega \subseteq \C $ is open and $P\in \C $, and if $f$ is a function defined and holomorphic in $\Omega \setminus \{P\}$, then we say that $f$ has an isolated singularity at $P$.

[Definition: Removable singularity] If $f$ has an isolated singularity at $P$ and if $f$ is defined and bounded on $D(P,r)\setminus \{P\}$ for some $r>0$, then we say that $f$ has a removable singularity at $P$.

Theorem 4.1.1. [The Riemann removable singularities theorem.] Suppose that $f$ has a removable singularity at $P$. Then $\lim _{z\to P}f(z)$ exists (and is a finite complex number), and the function

\begin{equation*}\widehat f(z)=\begin {cases} f(z), &z\in \Omega \setminus \{P\},\\\lim _{z\to P}f(z),&z=P\end {cases}\end{equation*}

(Observe that if the limit exists, then $\widehat f$ is continuous on $\Omega $ and holomorphic on $\Omega \setminus \{P\}$, so the fact that $\widehat f$ is holomorphic is simply Problem 1490.)

[Chapter 4, Problem 8a] Suppose that $P\in \Omega \subseteq \C $ for some open set $\Omega $. Suppose that $f:\Omega \setminus \{P\}\to \C $ is holomorphic and that $\lim _{z\to P} (z-P)f(z)=0$. Then $\lim _{z\to P}f(z)$ exists.

[Definition: Pole] If $f$ has an isolated singularity at $P$, and if $\lim _{z\to P}|f(z)|=\infty $, then we say that $f$ has a pole at $P$.

(Problem 2100) Suppose that $\Omega $ is an open set, $P\in \Omega $, $g:\Omega \to \C $ is holomorphic, $g(P)=0$, and $g\neq 0$ on $\Omega \setminus \{P\}$. Show that $f(z)=1/g(z)$ is holomorphic on $\Omega \setminus \{P\}$ and that $\lim _{z\to P} |f(z)|=\infty $.

(Problem 2110) Suppose that $P\in \Omega \subseteq \C $ for some open set $\Omega $. Suppose that $f:\Omega \setminus \{P\}\to \C $ is holomorphic and that $\lim _{z\to P} |f(z)|=\infty $. Let $W=\Omega \setminus \{z\in \Omega :f(z)=0\}$. Observe that $P\in W$. Show that $W$ is open.

[Chapter 4, Problem 15a] Let $f$ be as in the previous problem and let $g:W\setminus \{P\}\to \C $ be given by $g(z)=1/f(z)$. Then $g$ has a removable singularity at $P$ and $\lim _{z\to P} g(z)=0$.

[Definition: Essential singularity] If $f$ has an isolated singularity at $P$, and if $f$ has neither a pole nor a removable singularity at $P$, then we say that $f$ has an essential singularity at $P$.

(Problem 2111) State the precise $N$-$\delta $ negation of the statement “$\lim _{z\to P} |f(z)|=\infty $”.

(Problem 2120) Let $f:\C \setminus \{0\}\to \C $ be given by $f(z)=\exp (1/z)$. Let $w\in \C $ with $w\neq 0$ and let $r>0$. Show that $w=f(z)$ for some $z\in D(0,r)\setminus \{0\}$.

(Problem 2130) Show that if $r>0$ then $\sup _{0<|z|<r} |\exp (1/z)|=\infty $ and $\inf _{0<|z|<r} |\exp (1/z)|=0$. Conclude that $\lim _{z\to 0}|\exp (1/z)|$ does not exist (even in the sense of infinite limits).

Theorem 4.1.4. Suppose that $f$ has an essential singularity at $P$. Let $r>0$ be such that $D(P,r)\subseteq \Omega $. Then $f(D(P,r)\setminus \{P\})$ is dense in $\C $.

(Problem 2141) Show that if $f$ has an isolated singularity at $P$ and $\limsup _{z\to P}|f(z)|\neq \liminf _{z\to P} |f(z)|$ then $f$ has an essential singularity at $P$.

(Problem 2142) Show that if $f$ has an essential singularity at $P$ then $\limsup _{z\to P}|f(z)|=\infty $ and $\liminf _{z\to P} |f(z)|=0$.

(Problem 2150) Give an example of a $C^\infty $ function $f:\R \setminus \{0\}\to \R $ such that $\limsup _{x\to 0} |f(x)|=\infty $ and $\liminf _{x\to 0} |f(x)|=0$ but such that $f(x)\geq 0$ for all $x\in \R $.

4.2. Convergence of Laurent series

[Definition: Laurent series] A Laurent series is a formal expression of the form $\sum _{k=-\infty }^\infty a_k(z-P)^k$, where $P\in \C $ and each $a_k\in \C $, with the convention that $0^0=1$ and $0\cdot 0^k=0$ even if $k<0$.

[Definition: Convergence of Laurent series] We say that the Laurent series $\sum _{k=-\infty }^\infty a_k(z-P)^k$ converges at $z$ if the two series $\sum _{k=0}^\infty a_k(z-P)^k$ and $\sum _{k=1}^\infty a_{-k}(z-P)^{-k}$ both converge, and write

\begin{equation*}\sum _{k=-\infty }^\infty a_k(z-P)^k=\sum _{k=0}^\infty a_k(z-P)^k+\sum _{k=1}^\infty a_{-k}(z-P)^{-k}.\end{equation*}

Lemma 4.2.1. Suppose that the doubly infinite series $\sum _{k=-\infty }^\infty a_k(z-P)^k$ converges at $z=w_1$ and at $z=w_2$, where $0<|w_1-P|<|w_2-P|$. Then the series converges absolutely at $z$ for all $z$ such that $|w_1-P|<|z-P|<|w_2-P|$.

(Problem 2170) Suppose that the doubly infinite series $\sum _{k=-\infty }^\infty a_k(z-P)^k$ converges at $z=w$ and diverges at $z=\zeta $.

Lemma 4.2.2. Let $\sum _{k=-\infty }^\infty a_k(z-P)^k$ be a doubly infinite series that converges at $z=w$ for at least one $w\in \C \setminus \{P\}$. Then there are extended real numbers $r$ and $R$ with $0\leq r\leq |w-P|\leq R\leq \infty $ such that the series converges absolutely if $r<|z-P|<R$ and diverges if $|z-P|<r$ or $|z-P|>R$.

Furthermore, if $r<\tau <\sigma <R$ then the series converges uniformly on $\overline D(P,\sigma )\setminus D(P,\tau )$.

(Problem 2190) Establish the uniform convergence on $\overline D(P,\sigma )\setminus D(P,\tau )$ in Lemma 4.2.2.

(Problem 2200) Let $f(z)=\sum _{j=-\infty }^\infty a_j(z-P)^j$. Show that $f$ is holomorphic on $D(P,R)\setminus \overline D(P,r)$, where $r$ and $R$ are as in Lemma 4.2.2.

Proposition 4.2.4. Let $\sum _{j=-\infty }^\infty a_j(z-P)^j$ and $\sum _{j=-\infty }^\infty b_j(z-P)^j$ be doubly infinite series that both converge to the same value if $r<|z-P|<R$, for some $0\leq r<R\leq \infty $. Then $a_j=b_j$ for all $j$.

(Problem 2220) Suppose $f$ is holomorphic in $D(P,R)$ and that $0<\tau <R$. By Problem 1760 and Proposition 3.2.11, there is a unique sequence of complex numbers $\{a_k\}_{k=0}^\infty $ such that $f(z)=\sum _{k=0}^\infty a_k(z-P)^k$ for all $z\in D(P,R)$. Combine Theorem 3.3.1 with Theorem 3.1.1 to find a formula for $a_k$ in terms of an integral over $\partial D(P,\tau )$.

(Problem 2230) Let $\sum _{k=-\infty }^\infty a_k(z-P)^k$ be a doubly infinite series that converges to $f(z)$ if $r<|z-P|<R$, for some $0\leq r<R\leq \infty $. Let $r<\tau <R$. Compute

\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -P)^{n+1}}\,d\zeta \end{equation*}

4.3. Existence of Laurent Expansions

Theorem 4.3.2. Let $0\leq r<R\leq \infty $ and let $\Omega =D(P,R)\setminus \overline D(P,r)$ for some $P\in \C $. (We take $D(P,\infty )=\C $.)

Suppose that $f:\Omega \to \C $ is holomorphic. Then there exist constants $a_k$ such that the series

\begin{equation*}\sum _{k=-\infty }^\infty a_k(z-P)^k\end{equation*}

Furthermore, if $r<\sigma <\tau <R$ then the series converges uniformly on $\overline D(P,\tau )\setminus D(P,\sigma )$.

Theorem 4.3.1. Let $f$, $r$, $R$ be as in Theorem 4.3.2. If $r<\sigma <|z-P|<\tau <R$, then

\begin{equation*}f(z)=\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{\zeta -z}\,d\zeta -\frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}

(Problem 2240) Let $f$, $r$, $R$, $\sigma $, $\tau $, and $z$ be as in Theorem 4.3.1. We will use Theorem 4.3.1 to prove Theorem 4.3.2 (so you may not use Theorem 4.3.2). Begin the proof of Theorem 4.3.1 by computing

\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(z)}{\zeta -z} \,d\zeta - \frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \frac {f(z)}{\zeta -z} \,d\zeta .\end{equation*}

(Problem 2250) Let $r<\sigma <|z-P|<\tau <R$. Complete the proof of Theorem 4.3.1 by computing

\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )-f(z)}{\zeta -z} \,d\zeta - \frac {1}{2\pi i} \oint _{\partial D(P,\sigma )} \frac {f(\zeta )-f(z)}{\zeta -z} \,d\zeta .\end{equation*}

(Problem 2260) Let $f$, $r$, $R$ be as in Theorem 4.3.2. We seek to show that $f$ may be represented by a Laurent series. By Problem 2230, the only possible Laurent series is $\sum _{k=-\infty }^\infty a_k(z-P)^k$, where

\begin{equation*}a_k=\frac {1}{2\pi i} \oint _{\partial D(P,\tau )} \frac {f(\zeta )}{(\zeta -P)^{k+1}}\,d\zeta \end{equation*}

for any $\tau \in (r,R)$. Begin the proof of Theorem 4.3.2 by showing that the sum $\sum _{k=-\infty }^\infty a_k(z-P)^k$ converges absolutely for all $z\in \Omega $. (By Problem 2190, this means that the series converges uniformly on compact subsets of $\Omega $.) Hint: Let $r<\sigma <|z-P|<\tau <R$ and find upper bounds on $a_k$ in terms of $M_\tau =\sup _{\partial D(P,\tau )}|f|$ and $M_\sigma =\sup _{\partial D(P,\sigma )}|f|$.

(Problem 2270) Continue the proof of Theorem 4.3.2 by showing that, if $r<\sigma <|z-P|<\tau <R$, then

\begin{equation*}\sum _{k=0}^\infty a_k(z-P)^k = \frac {1}{2\pi i}\oint _{\partial D(P,\tau )} \frac {f(\zeta )}{\zeta -z}\,d\zeta .\end{equation*}

4.3. The Laurent series near an isolated singularity

Proposition 4.3.3. Suppose that $f$ is holomorphic in the punctured disc $\Omega =D(P,R)\setminus \{P\}$ for some $P\in \C $ and some $0<R\leq \infty $. Then $f$ has a unique Laurent series

\begin{equation*}f(z)=\sum _{k=-\infty }^\infty a_k(z-P)^k\end{equation*}

which converges absolutely to $f(z)$ for all $z\in D(P,R)\setminus \{P\}$. The convergence is uniform on compact subsets of $D(P,R)\setminus \{P\}$. The coefficients are given by

\begin{equation*}a_k=\frac {1}{2\pi i}\oint _{\partial D(P,\sigma )} \frac {f(\zeta )}{(\zeta -P)^{k+1}}\,d\zeta \end{equation*}

(Problem 2290) Suppose that $f$ has a removable singularity at $P$. Show that $a_k=0$ for all $k<0$.

(Problem 2300) Suppose that $a_k=0$ for all $k<0$. Show that $f$ has a removable singularity at $P$.

[Definition: Order of a zero] Suppose that $f$ is holomorphic in $D(P,r)$ for some $r>0$ and $f(P)=0$. Then $f(z)=\sum _{k=0}^\infty a_k (z-P)^k$ for all $z\in D(P,r)$. The order of the zero of $f$ at $P$ is the smallest $n$ such that $a_n\neq 0$; note that the order is at least $1$.

[Chapter 4, Problem 15b] Suppose that $f$ is holomorphic in $D(P,R)\setminus \{P\}$ and that $f$ has a pole at $P$. Then $1/f$ is holomorphic in $D(P,r)\setminus \{P\}$ for some $r>0$, has a removable singularity at $P$, and the holomorphic extension $g$ of $1/f$ to $D(P,r)$ satisfies $g(P)=0$. Let $n$ be the order of the zero of $g$ at $P$. Then $(z-P)^n f(z)$ has a removable singularity at $P$.

(Problem 2310) Suppose that $f$ has a pole at $P$. Show that there is some $N>0$ such that $a_{-N}\neq 0$ and such that $a_k=0$ for all $k<-N$.

[Chapter 4, Problem 15c] Suppose that $f$ is holomorphic in $D(P,R)\setminus \{P\}$, that $f$ is not bounded in $D(P,R/2)\setminus \{P\}$, and that there is a $m\in \N $ such that the function $g$ given by $g(z)=(z-P)^m f(z)$ is bounded in $D(P,R/2)$. Show that $f$ has a pole at $P$.

(Problem 2320) Suppose that there is some $N>0$ such that $a_{-N}\neq 0$ and such that $a_k=0$ for all $k<-N$. Show that $f$ has a pole at $P$.

[Definition: Order of a pole] Suppose that $f$ has a pole at $P$. Then there is some $N>0$ such that $a_{-N}\neq 0$ and such that $f(z)=\sum _{k=-N}^\infty a_k (z-P)^k$ for all $z$ in a punctured neighborhood of $P$ (that is, for all $z$ in in $D(P,r)\setminus \{P\}$ for some $r>0$). We call $N$ the order of the pole at $P$. If $N=1$ we say that $f$ has a simple pole at $P$.

[Definition: Pole/zero of nonpositive order] If you write “pole of order 0”, I will assume that you mean “removable singularity”. If you write “zero of order 0 at $P$”, I will assume that you mean “holomorphic near $P$ and nonzero at $P$.” If you write “zero/pole of order $-n$”, for $n\in \N $, I will assume that you mean a pole/zero of order $n$ (possibly after the additional step of applying the Riemann removable singularities theorem).

(Problem 2330) Show that $f$ has an essential singularity at $P$ if and only if, for all $N>0$, there is a $k\in \Z $ with $k<-N$ such that $a_k\neq 0$.

4.4. Examples of Laurent Expansions

(Problem 2340) Suppose that $f$ has a zero of order $k$ at $P$. Show that $\frac {1}{(z-P)^k}f(z)$ has a removable singularity at $P$ and that its limit at $P$ is not zero.

(Problem 2350) Suppose that $f$ has a pole of order $n$ at $P$. Show that $(z-P)^nf(z)$ has a removable singularity at $P$ and that its limit at $P$ is not zero.

(Problem 2360) Suppose that $f$ is holomorphic in $D(P,r)\setminus \{P\}$ and that $(z-P)^kf(z)$ has a removable singularity at $P$ for $k\in \N $. Show that either $f$ has a removable singularity at $P$ or $f$ has a pole of order at most $k$ at $P$. If in addition $\lim _{z\to P} (z-P)^k f(z)\neq 0$ then $f$ has a pole of order exactly $k$.

[Chapter 4, Problem 29] Suppose that $f$ has a pole of order $n> 0$ at $P$. Let $k\geq -n$ be an integer. Let the Laurent series for $f$ in a punctured neighborhood of $P$ be $\sum _{k=-n}^\infty a_k (z-P)^k$. Show that

\begin{equation*}a_k=\lim _{z\to P}\frac {1}{(n+k)!} \biggl (\frac {\partial }{\partial z}\biggr )^{n+k}((z-P)^nf(z)) .\end{equation*}

(Bonus Problem 2361) Suppose that $f$ is holomorphic in $D(P,r)\setminus \{P\}$ for some $P\in \C $, $r>0$, and that

\begin{equation*}\frac {1}{(\ell +k)!} \biggl (\frac {\partial }{\partial z}\biggr )^{\ell +k}((z-P)^\ell f(z))\end{equation*}

has a removable singularity at $z=P$ for some integers $k$ and $\ell $ with $k+\ell \geq 0$. Show that $f$ has a removable singularity or pole of order at most $\ell $ at $P$ and that

\begin{equation*}a_k=\lim _{z\to P}\frac {1}{(\ell +k)!} \biggl (\frac {\partial }{\partial z}\biggr )^{\ell +k}((z-P)^\ell f(z)).\end{equation*}

(Problem 2370) Suppose that $f$ is holomorphic in $D(P,r)\setminus \{P\}$ and that $(z-P)^\ell f(z)$ has a removable singularity at $P$ for some $\ell \geq 0$. Let $f(z)=\sum _{k=-\infty }^\infty a_k (z-P)^k$ in $D(P,r)\setminus \{P\}$. Show that

\begin{equation*}a_k=\lim _{z\to P} \Bigl ((z-P)^{-k}f(z)-\sum _{n=-\ell }^{k-1} a_n (z-P)^{n-k}\Bigr ).\end{equation*}

[Definition: Principal part] The principal part of the Laurent series $\sum _{k=-\infty }^\infty a_k(z-P)^k$ is $\sum _{k=-\infty }^{-1} a_k(z-P)^k$.

(Problem 2380) Let $f(z)=z/(z-1)$. Find the Laurent series for $f$ about $z=1$ by direct computation.

(Problem 2390) Find the Laurent series for $f(z)=z/(z-1)$ at $P=1$ by using Problem 4.29.

(Problem 2400) Find the Laurent series for $f(z)=\frac {e^z}{(z-2)^2}$ at $P=2$.

(Problem 2410) Find the principal part of the Laurent series for $f(z)=\frac {e^z}{(z-1)(z-3)^2}$ at $P=3$.

(Problem 2420) Find the principal part of the Laurent series for $f(z)=\frac {e^z}{\sin z}$ at $z=0$.

4.5. Real Analysis

(Memory 2430) Let $(X,d)$ be a metric space and let $Y\subset X$ be a closed subset. Suppose that $F\subseteq Y$ is relatively closed, that is, closed in $(Y,d)$. Show that $F$ is also closed in $(X,d)$.

(Memory 2440) Let $(X,d)$ be a metric space and let $Y\subset X$ be an open subset. Suppose that $G\subseteq Y$ is relatively open, that is, open in $(Y,d)$. Show that $G$ is also open in $(X,d)$.

4.5. The index of a curve around a point

(Problem 2450) Let $r:[0,1]\to (0,\infty )$ and $\theta :[0,1]\to \R $ be two $C^1$ functions. Let $\psi (t)=r(t)e^{i\theta (t)}$. Show that $\theta '(t)=\im (\psi '(t)/\psi (t))$ and $r'(t)/r(t)=\re (\psi '(t)/\psi (t))$.

(Problem 2460) Suppose that $\psi $ is a closed curve. What can you say about $r(0)$, $r(1)$, $\theta (0)$, and $\theta (1)$? What is the geometrical significance of the number $\frac {1}{2\pi }(\theta (1)-\theta (0))$?

\begin{equation*}\frac {1}{2\pi }(\theta (1)-\theta (0))=\frac {1}{2\pi i} \oint _\psi \frac {d\zeta }{\zeta }.\end{equation*}

We call this number the index of $\psi $ with respect to $0$, or the winding number of $\psi $ about $0$.

(Lemma 2471) Suppose $\gamma :[0,1]\to \C \setminus \{0\}$ is a $C^1$ curve. Then there exist two $C^1$ functions $r:[0,1]\to (0,\infty )$ and $\theta :[0,1]\to \R $ such that $\gamma (t)=r(t)e^{i\theta (t)}$ for all $t\in [0,1]$.

(Problem 2480) Begin the proof of Lemma 2471 by letting $r(t)=|\gamma (t)|$ and showing that $r$ is a $C^1$ function. (In particular, show that $\frac {r'(t)}{r(t)}=\re \frac {\gamma '(t)}{\gamma (t)}$.)

(Problem 2490) Show that there exists a $C^1$ function $\theta :[0,1]\to \R $ such that $\gamma (t)=r(t)e^{i\theta (t)}$ for all $t$, where $r(t)=|\gamma (t)|$ as in the previous problem. Hint: There is a $\theta _0\in \R $ such that $\gamma (0)=r(0)e^{i\theta _0}$. What do you think $\theta '(t)$ ought to equal?

Lemma 4.5.5. Let $\gamma $ be a $C^1$ closed curve and let $P\in \C \setminus \widetilde \gamma $. Then

\begin{equation*}\frac {1}{2\pi i}\oint _\gamma \frac {1}{\zeta -P}\,d\zeta \end{equation*}

Definition 4.5.4. We define $\Ind _\gamma (P)=\frac {1}{2\pi i}\oint _\gamma \frac {1}{\zeta -P}\,d\zeta $; this is the index of $\gamma $ with respect to $P$, or the winding number of $\gamma $ about $P$.

[Definition: Simply connected] A connected open set $\Omega \subseteq \C $ is simply connected if, whenever $\gamma :[0,1]\to \Omega $ is a closed curve, we have that $\gamma $ is homotopic to a point (that is, to some constant function $\gamma _0:[0,1]\to \C $).

(Problem 2510) Suppose that $\Omega $ is simply connected, $\gamma :[0,1]\to \Omega $ is a $C^1$ closed curve, and $P\in \C \setminus \widetilde \gamma $ satisfies $\Ind _\gamma (P)\neq 0$. Show that $P\in \Omega $.

(Problem 2520) Let $\gamma :[0,1]\to \C $ be a $C^1$ closed curve. Show that $\Ind _\gamma $ is a continuous function on $\C \setminus \widetilde \gamma $.

(Problem 2530) Show that $\Ind _\gamma $ is constant on every connected component of $\C \setminus \widetilde \gamma $.

(Problem 2540) Suppose that $\gamma _1$ and $\gamma _2$ are homotopic closed curves in $\C \setminus \{P\}$. Show that $\Ind _{\gamma _1}(P)=\Ind _{\gamma _2}(P)$.

(Problem 2550) Show that if $\widetilde \gamma =\partial D(P,r)$ is a circle traversed once counterclockwise, then $\Ind _\gamma (z)=1$ if $z\in D(P,r)$ and $\Ind _\gamma (z)=0$ if $z\notin \overline D(P,r)$.

(Bonus Problem 2560) Let $t\in (0,1)$ be such that $\gamma '(t)\neq 0$. Let $r>0$ be such that if $z\in \overline D(\gamma (t),r)$ then $z=\gamma (s)$ for at most one $s\in [0,1]$. Show that there is some $s>0$ such that, if $\tau \in \R $ and $|\tau |<s$, then $\gamma (t)+i\tau \gamma '(t)\notin \widetilde \gamma $.

(Bonus Problem 2570) Show that for such $\tau $ we have that $\Ind _\gamma (\gamma (t)+i\tau \gamma '(t))=\Ind _\gamma (\gamma (t)-i\tau \gamma '(t))+1$.

4.5. The Calculus of Residues

[Definition: Simply connected open set] An open set $\Omega \subseteq \C $ is simply connected if every closed curve $\gamma :[0,1]\to \Omega $ is homotopic to a point (that is, to a constant curve).

[Definition: Residue] If $\Omega \subseteq \C $ is open, $P\in \Omega $, and $f:\Omega \setminus \{P\}\to \C $ is holomorphic, then $\Res _f(P)$ is defined to be the coefficient of $(z-P)^{-1}$ in the Laurent expansion of $f$ about $P$.

Theorem 4.5.3. Suppose that $\Omega \subseteq \C $ is open and simply connected, $\{P_1,P_2,\dots ,P_n\}\subset \Omega $ is a set of $n$ distinct points, $\gamma :[0,1]\to \Omega \setminus \{P_1,P_2,\dots ,P_n\}$ is a $C^1$ closed curve, and $f:\Omega \setminus \{P_1,P_2,\dots ,P_n\}$ is holomorphic. Then

\begin{equation*}\oint _\gamma f=2\pi i\sum _{k=1}^n \Res _f(P_k)\cdot \Ind _\gamma (P_k).\end{equation*}

(Memory 2580) By Problem 1450, Theorem 4.5.3 is true in the special case where $n=0$, that is, where $f$ is holomorphic in all of $\Omega $.

(Problem 2590) Prove Theorem 4.5.3 in the special case where $n=1$ and where the Laurent series for $f$ about $P=P_1$ converges uniformly on $\widetilde \gamma $.

(Problem 2600) Suppose that $\Omega \subseteq \C $ is open, $P\in \Omega $, and $f:\Omega \setminus \{P\}\to \C $ is holomorphic. Show that the principal part of the Laurent series for $f$ at $P$ converges absolutely for all $z\in \C \setminus \{P\}$ to a function holomorphic in $\C \setminus \{P\}$.

(Problem 2601) Suppose that $h$ is holomorphic in $D(P,r)$ and that $g$ is holomorphic in $D(P,r)\setminus \{P\}$. If $f=g+h$ in $D(P,r)\setminus \{P\}$, show that $\Res _f(P)=\Res _g(P)$.

4.6. Applications of the Calculus of Residues to the Calculation of Definite Integrals and Sums

(Memory 2620) By Problem 4.29, if $f$ has a pole of order $k$ at $P$, then

\begin{equation*}\Res _f(P)=\frac {1}{(k-1)!} \biggl (\frac {\partial }{\partial z}\biggr )^{k-1}((z-P)^kf(z))\bigg \vert _{z=P}.\end{equation*}

\begin{equation*}\Res _f(P)=\lim _{z\to P}(z-P)f(z).\end{equation*}

[Chapter 3, Problem 22] L’Hôpital’s rule is valid for quotients of meromorphic functions.

That is, let $r>0$ and $P\in \C $. Suppose that $f$ and $g$ are both holomorphic in $D(P,r)\setminus \{P\}$, and that neither $f$ nor $g$ has an essential singularity at $P$. Finally suppose that $g$ is not a constant in $D(P,r)\setminus \{P\}$.

Then there is a $\varrho $ with $0<\varrho \leq r$ such that $g(z)\neq 0\neq g'(z)$ for all $z\in D(P,\varrho )\setminus \{P\}$. Furthermore, the functions $f/g$ and $f'/g'$, which are holomorphic in $D(P,\varrho )\setminus \{P\}$, do not have essential singularities at $P$.

Finally, if $f$ and $g$ both have poles at $P$ or if $\lim _{z\to P} f(z)=0=\lim _{z\to P} g(z)$, then $f/g$ has a pole at $P$ if and only if $f'/g'$ has a pole at $P$, and if $f'/g'$ has a removable singularity then $\lim _{z\to P} f(z)/g(z)=\lim _{z\to P} f'(z)/g'(z)$.

(Problem 2630) Consider the integral $\int _{-\infty }^\infty \frac {x^2}{x^4+4}\,dx$. Write down a family of closed $C^1$ curves $\gamma _R$ and a function $f$ holomorphic in a neighborhood of $\widetilde \gamma _R$ such that $\lim _{R\to \infty }\oint _{\gamma _R} f=\int _{-\infty }^\infty \frac {x^2}{x^4+4}\,dx$.

Then find $\int _{-\infty }^\infty \frac {x^2}{x^2+4} dx$ by finding $\oint _{\psi _R} f$ for all $R$ large enough.

(Problem 2640) Compute $\int _{-\infty }^\infty \frac {\cos x}{x^2+4} \,dx$. Hint: Recall that $\re \int _a^b f(x)\,dx=\int _a^b \re f(x)\,dx$.

(Problem 2650) Compute $\int _{0}^\infty \frac {\sin x}{x}\,dx$ by finding an appropriate function $f$ and closed contour $\gamma _{R,S}$ that satisfies $\oint _{\gamma _{R,S}} f=0$. (This is the exercise immediately after Example 4.6.3 in your book; a verbatim presentation of Example 4.6.3 will not be accepted.)

(Problem 2660) Let $n\in \N $ and let $\theta _0\in \R $. Define $z^{1/n}$ with branch cut at angle $\theta _0$ by $(re^{i\theta })^{1/n}=r^{1/n} e^{i\theta /n}$ for all $r>0$ and all $\theta _0\leq \theta <\theta _0+2\pi $. Show that $z^{1/n}$ is well defined and holomorphic on $\C \setminus \{te^{i\theta _0}:t\in \R ,\>t\geq 0\}$ and that $\p {z} z^{1/n}=\frac {1}{n (z^{1/n})^{n-1}}$.

(Problem 2680) Use the calculus of residues to compute $\int _0^\infty \frac {dx}{x^2+5x+6}$.

4.6. Calculation of Sums

(Problem 2710) Let $\cot z=\frac {\cos z}{\sin z}$. Show that $\cot $ is holomorphic on $\C \setminus \{n\pi :n\in \Z \}$ and that $\Res _{\cot {}}(n\pi )=1$ for all $n\in \Z $.

(Problem 2720) Show that $\cot (x+iy)$ converges to $-i$ as $y\to \infty $ and to $i$ as $y\to -\infty $, uniformly in $x\in \R $.

(Problem 2730) Show that if $y\in \R $ and $x=(n+1/2)\pi $ for some $n\in \Z $, then $|\cot (x+iy)|\leq 1$ for all $y\in \R $.

(Problem 2740) We would like to compute $\sum _{n=1}^\infty \frac {1}{n^2}$. In this problem we begin the proof. Let $\gamma _n:[0,1]\to \C $ be a $C^1$ parameterization of the rectangle with corners at $\pm (n\pi +\frac {\pi }{2})\pm in$, for $n\in \N $. Let $f(z)=\frac {\cot z}{z^2}$. Show that $\lim _{n\to \infty } \oint _{\gamma _n} f=0$.

(Problem 2760) Find all the singularities of $f$ and then find the residues of $f$ at each singularity.

(Problem 2770) Use the above results to compute $\sum _{j=1}^\infty \frac {1}{j^2}$.

4.7. Real analysis

(Problem 2780) Let $X=\C \cup \{\infty \}$ (where $\infty $ is a single point not in $\C $) and define $d:X\times X\to [0,\infty )$ by

\[d(z,w)=\begin {cases} \qquad 0, & z=\infty =w,\\ \quad \frac {2}{\sqrt {1+|z|^2}}, & z\in \C ,\>w=\infty ,\\ \quad \frac {2}{\sqrt {1+|w|^2}}, & w\in \C ,\>z=\infty ,\\ \frac {2|z-w|}{\sqrt {1+|z|^2}\sqrt {1+|w|^2}}, &z\in \C ,\>w\in \C . \end {cases}\]

This is called the spherical metric on $X$. Then $(X,d)$ is a metric space. (See Problem 4.32 in your book.)

This metric arises as follows. If $z=\xi +i\eta $, where $\xi $, $\eta \in \R $, then we let the stereographic projection $p(z)$ be the point in $\R ^3$ that lies on the unit sphere $\{(x,y,t):x^2+y^2+t^2=1\}$ and also lies on the line through $(0,0,1)$ (the north pole) and the point $(x,y,0)$. See the following figure. Then $d(z,w)=\|p(z)-p(w)\|$ (if $z$, $w\in \C $ and $\|\,\cdot \,\|$ denotes the standard Euclidean metric in $\R ^3$) and $d(z,\infty )=\|(0,0,1)-p(z)\|$.

(Problem 2790) The subspace $(\C ,d)$ is equivalent to $(\C ,|\cdot -\cdot |)$ (that is, $\C $ equipped with the standard metric) in the sense that, if $x$, $x_n\in \C $, then $x_n\to x$ in $(\C ,d)$ if and only if $x_n\to x$ in $(\C ,|\cdot -\cdot |)$.

(Problem 2800) The subspace $(\C ,d)$ is equivalent to $(\C ,|\cdot -\cdot |)$ in the sense that if $z\in \Omega \subseteq \C $ and $f$ is a function defined on $\Omega $, then $f$ is continuous at $z$ as a function on $(\Omega ,d)$ if and only if $f$ is continuous at $z$ as a function on $(\Omega ,|\cdot -\cdot |)$.

(Problem 2810) The subspace $(\C ,d)$ is equivalent to $(\C ,|\cdot -\cdot |)$ in the sense that if $f:Y\to \C $ is a function defined on a metric space $Y$ and $a\in Y$, then $f$ is continuous at $a$ as a function mapping into $(X,d)$ (or $(\C ,d)$) if and only if $f$ is continuous at $a$ as a function mapping into $(\C ,|\cdot -\cdot |)$.

(Problem 2820) If $\{x_n\}_{n=1}^\infty \subset \C $, then $x_n\to \infty $ in $(X,d)$ if and only if $\lim _{n\to \infty } |x_n|=\infty $ in the sense of real analysis.

(Problem 2830) If $\Omega \subseteq \C $ is unbounded and $f:\Omega \to Y$ for some metric space $(Y,\rho )$, we may define $\lim _{z\to \infty } f(z)$ in $(\C ,|\cdot -\cdot |)$ as follows: $\lim _{z\to \infty } f(z)=L$ if, for every $\varepsilon >0$, there is a $N>0$ such that if $z\in \Omega $ and $|z|>N$, then $\rho (f(z),L)<\varepsilon $. Show that $\lim _{z\to \infty } f(z)=L$ in $(\C ,|\cdot -\cdot |)$ if and only if $\lim _{z\to \infty } f(z)=L$ in $(X,d)$.

(Problem 2840) If $(Y,\rho )$ is a metric space, $a\in Y$, and $f:Y\setminus \{a\}\to C$, then we say that $\lim _{y\to a} f(y)=\infty $ in $(\C ,|\cdot -\cdot |)$ if for every $R>0$ there is a $\delta >0$ such that if $0<\rho (a,y)<\delta $ then $|f(y)|>R$. Show that $\lim _{y\to a} f(y)=\infty $ in $(\C ,|\cdot -\cdot |)$ if and only if $\lim _{y\to a} f(y)=\infty $ in $(X,d)$.

4.7. Meromorphic Functions

Definition 4.7.2. Let $\Omega \subseteq \C $ be open. A function $f$ is said to be meromorphic on $\Omega $ if there is a set $S$ such that

Recall [Problem 2050]: Let $\Omega $ be a connected open set and let $f:\Omega \to \C $ be holomorphic and not constant. Then the set $S=\{z\in \Omega :f(z)=0\}\subset \Omega $ has no accumulation points in $\Omega $.

(Problem 2850) Let $\Omega \subseteq \C $ be open and let $S\subset \Omega $ have no accumulation points in $\Omega $. Show that $\Omega \setminus S$ is both open and dense in $\Omega $.

[Chapter 3, Problem 42 (generalized)] Let $K\subset \Omega $ be compact. Then $K\cap S$ is finite.

(Problem 2860) Suppose in addition that $\Omega $ is connected. Show that $\Omega \setminus S$ is connected.

(Problem 2870) If $\Omega \subseteq \C $ is open, and if $S$ and $Z$ are two subsets of $\Omega $ with no accumulation points in $\Omega $, show that $S\cup Z$ has no accumulation points in $\Omega $.

In particular, let $f$ be meromorphic and non-constant in $\Omega $ for some $\Omega \subseteq \C $ open and connected. Let $S$ be the singular set for $f$ and let $Z=\{z\in \Omega \setminus S:f(z)=0\}$ be the zero set. Show that $S\cup Z$ has no accumulation points in $\Omega $.

[Chapter 4, Problem 64a] The product of two meromorphic functions is meromorphic.

(Problem 2880) Show that the derivative of a meromorphic function is meromorphic.

[Chapter 4, Problem 64b] Suppose that $f$ is meromorphic in $\Omega $. Then the function obtained by extending $1/f$ as much as possible using the Riemann removable singularities theorem is meromorphic in $\Omega $.

(Problem 2890) Suppose that $\Omega $, $W\subseteq \C $ are open and connected, that $f:\Omega \to W$ is holomorphic and not constant, and that $g:W\to \C $ is meromorphic in $W$. Show that $g\circ f$ is meromorphic in $\Omega $.

(Problem 2891) Suppose that $\Omega \subseteq \C $ is open and that $S\subset \Omega $ has no accumulation points in $\Omega $. Show that $f$ is meromorphic in $\Omega $ with singular set $S$ if and only if $f$ is holomorphic in $\Omega \setminus S$ and if the function $\hat f$ given by

is continuous as a function from $\Omega $ to $(X,d)$, where $(X,d)$ is the metric space in Problem 2780.

4.7. Singularities at Infinity

Definition 4.7.4. Let $\Omega \subseteq \C $ be open. Suppose that there is some $R>0$ such that

\begin{equation*}\C \setminus \overline D(0,R) = \{z\in \C :|z|>R\}\subseteq \Omega .\end{equation*}

If $f$ is holomorphic on $\Omega $, then we say that $f$ has an isolated singularity at $\infty $.

Let $W=\{z\in \C \setminus \{0\}:1/z\in \Omega \}$ and define $g:W\to \C $ by $g(z)=f(1/z)$.

If $f$ has a removable singularity or pole at $\infty $, we say that $f$ is meromorphic at $\infty $.

Recall [Theorem 4.3.2]: If $f$ is holomorphic on an open set $\Omega $, and $\Omega \supseteq D(0,\infty )\setminus \overline D(0,R)=\{z\in \C :|z|>R\}$, then there is a unique Laurent series $\sum _{n=-\infty }^\infty a_n z^n$ that converges to $f$ on $\{z\in \C :|z|>R\}$.

[Definition: Laurent expansion around infinity] If there is an $R>0$ such that $\sum _{n=-\infty }^\infty a_n z^n$ that converges to $f$ on $\{z\in \C :|z|>R\}$, then we call $\sum _{n=-\infty }^\infty a_n z^n$ the Laurent expansion of $f$ around $\infty $.

(Problem 2910) Let $\Omega $, $W\subset \C $ be open. Suppose that $f$ is meromorphic and not constant in $\Omega $ and that $g$ is meromorphic in $W$. If $f$ has any poles, we require that $g$ be meromorphic at $\infty $; that is, there is an $R>0$ such that$\{z\in \C :|z|>R\}\subseteq W$ and $g$ has no poles in $\{z\in \C :|z|>R\}$, and furthermore that $g$ has either a removable singularity or a pole at $\infty $. Suppose furthermore that $f(\Omega \setminus S_f)\subseteq W$ where $S_f$ is the singular set for $f$. Show that $g\circ f$ is meromorphic on $\Omega $ (possibly after “filling in” removable singularities).

(Problem 2920) Suppose that $\Omega \subseteq \C $ is open and that $S\subset \Omega $ has no accumulation points in $\Omega $. Further suppose that there is some $R>0$ such that $\{z\in \C :|z|>R\}\subseteq \Omega \setminus S$. Show that $f$ is meromorphic in $\Omega $ and at $\infty $ with singular set $S$ if and only if $f$ is holomorphic in $\Omega \setminus S$ and if the function $\hat f$ given by

\[\hat f(z)=\begin {cases} f(z),&z\in \Omega \setminus S,\\\infty , &z\in S,\\\lim _{\zeta \to \infty } f(\zeta ),&z=\infty \end {cases}\]

is continuous as a function from $\Omega \cup \{\infty \}\subseteq X$ (with the metric $d$) to $(X,d)$, where $(X,d)$ is the metric space in Problem 2780.

Theorem 4.7.5. Suppose that $f:\C \to \C $ is entire and is also meromorphic at $\infty $. Then $f$ is a polynomial.

Theorem 4.7.7. Suppose that $f$ is meromorphic in $\C $ and also is meromorphic at $\infty $. Then there are two polynomials $p$ and $q$ such that the singular set of $f$ is equal to the zero set of $q$ and such that $f(z)=\frac {p(z)}{q(z)}$ for all $z$ in $\C $ outside of the singular set.

5.1. Counting Zeros and Poles

Theorem 5.1.4. (Argument principle for meromorphic functions.) Let $\Omega \subseteq \C $ be open and let $f$ be meromorphic in $\Omega $. Let $\overline D(P,r)\subset \Omega $. Suppose that $f$ has no poles on $\partial D(P,r)$ and that $f(z)\neq 0$ for all $z\in \partial D(P,r)$. Then

\begin{equation*}\frac {1}{2\pi i} \oint _{\partial D(P,r)} \frac {f'}{f} = \sum _{j=1}^p n_j-\sum _{k=1}^q m_k, \end{equation*}

where $n_1,\dots n_p$ are the multiplicities of the zeroes $z_1,\dots ,z_p$ of $f$ in $D(P,r)$ and where $m_1,\dots m_q$ are the orders of the poles $w_1,\dots ,w_q$ of $f$ in $D(P,r)$.

[Chapter 5, Problem 1] Suppose that $\Omega \subseteq \C $ is open, $f$ is meromorphic in $\Omega $, and $\overline D(P,r)\subset \Omega $. Then $f$ has at most finitely many poles and at most finitely many zeroes in $\overline D(P,r)$.

(Problem 2950) In this problem we will prove Theorem 5.1.4. Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be meromorphic and not uniformly zero. Let $g(z)=\frac {f'(z)}{f(z)}$; then $g$ is meromorphic in $\Omega $.

(Problem 2960) Write down a version of the argument principle that allows us to count the number of solutions to $f(z)=3$ in $D(P,r)$.

5.2. The Local Geometry of Holomorphic Functions

Recall [Problem 1140]: If $\gamma $ is a $C^1$ curve and $f$ is holomorphic in a neighborhood of $\widetilde \gamma $ then $f\circ \gamma $ is also a $C^1$ curve. Clearly, if $\gamma $ is closed then so is $f\circ \gamma $.

(Problem 2970) Suppose that $\gamma $ is the standard counterclockwise parameterization of $\partial D(P,r)$, that $f$ is holomorphic in $D(P,R)$ for some $R>r$, and that $f(\partial D(P,r))\subset \C \setminus \{0\}$. Show that $\Ind _{f\circ \gamma }(0)$ is equal to the number of solutions to $f(z)=0$ in $D(P,r)$ (counted with multiplicity). Hint: Use the argument principle.

(Problem 2980) You are given that $f$ is holomorphic in $D(0,2)$ and that there are at most finitely many points $w$ such that $f(z)=w$ for more than one $z\in \partial D(0,1)$. Illustrated are the three points $0$, $-3$, and $5$ and the set $f(\partial D(0,1))$. Counted with multiplicity, how many solutions are there to the equation $f(z)=-3$ in the unit disc? How many solutions are there to the equation $f(z)=5$ in the unit disc?

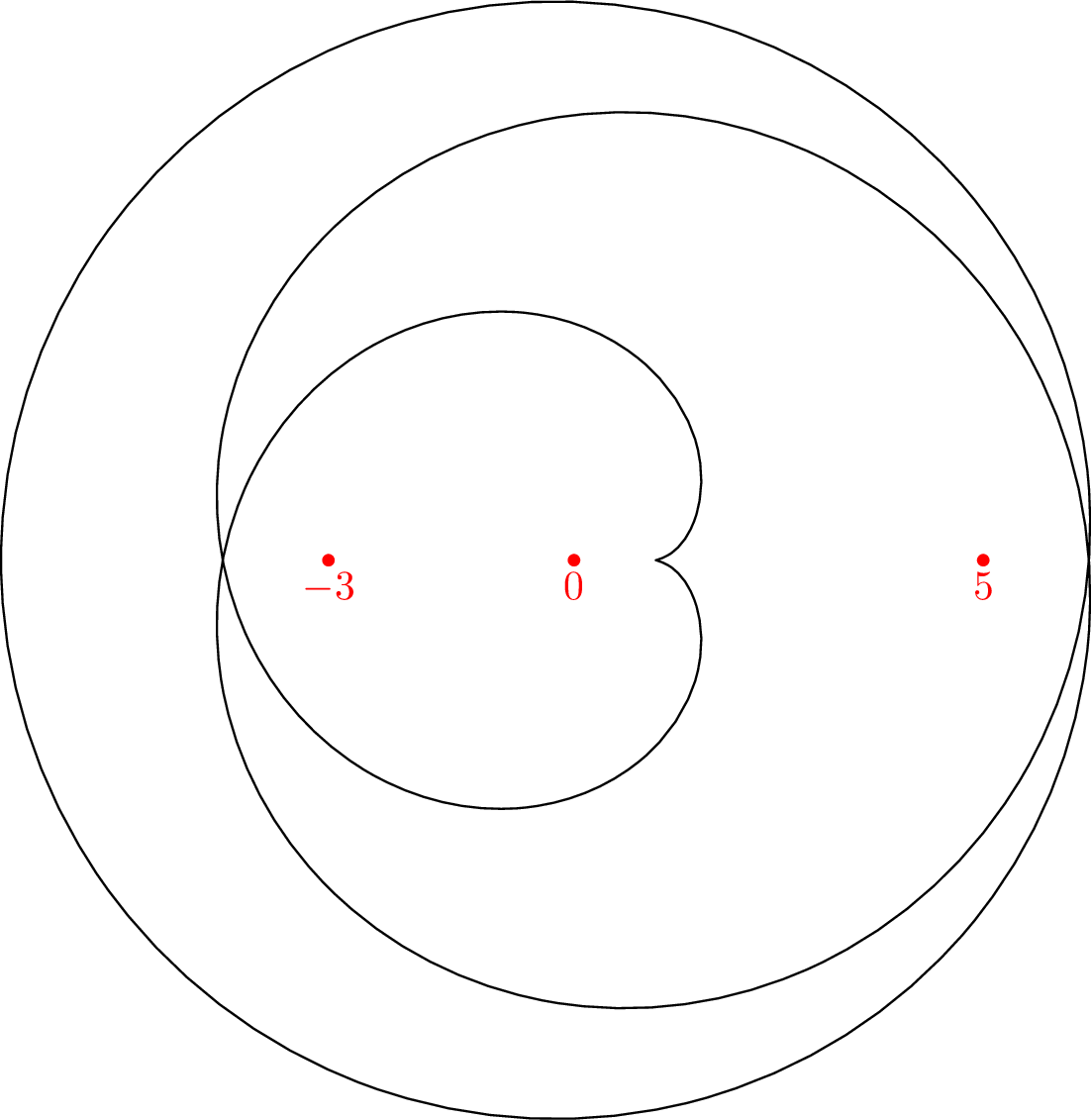
(Problem 2990) For the function $f$ illustrated above, the only solution to $f(z)=0$ in $D(0,1)$ is $z=0$. How is this possible?

(Problem 3000) You are given that $g$ is holomorphic in $D(0,2)$. Illustrated is the point $0$ and the set $g(\partial D(0,1))$. You are given that there are four solutions to the equation $g(z)=0$ in $D(0,1)$. How is this possible?

5.2. Real Analysis

Recall [Problem 850]: Let $X$ be a compact metric space and let $f:X\to Z$ be a continuous function. Then $f(X)$ is compact.

(Memory 3010) Let $K\subseteq \C $ be compact and let $\Omega \subseteq \C $ be a connected component of $\C \setminus K$. Then $\Omega $ is open.

5.2. The Open Mapping Theorem

Theorem 5.2.1. (The open mapping theorem.) Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic. Then either $f(\Omega )=\{Q\}$ for some $Q\in \C $ or $f(\Omega )$ is an open subset of $\C $.

(Problem 3020) In this problem we begin the proof of Theorem 5.2.1. Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic and not constant. Let $P\in \Omega $ and let $Q=f(P)$. Show that if $r>0$ and $\overline D(P,r)\subset \Omega $, and if $\gamma (t)=P+re^{it}$, $0\leq t\leq 2\pi $, then $\Ind _{f\circ \gamma }(Q)>0$.

(Problem 3040) Let $\Omega $ be the connected component of $\C \setminus f(\partial D(P,r))$ containing $Q$. Show that $U\subseteq f(\Omega )$.

(Problem 3050) [Prove the open mapping theorem.] Show that $f(\Omega )$ is open.

(Problem 3060) Give an example of an open set $\Omega \subseteq \R ^2$ and a non-constant $C^\infty $ function $f:\Omega \to \R ^2$ such that $f(\Omega )$ is not open.

(Problem 3061) Let $\Omega \subset \C $ be open, connected, and bounded, and let $f:\overline \Omega \to \C $ be continuous on $\overline \Omega $ and holomorphic in $\Omega $. Show that $\partial (f(\Omega ))\subseteq f(\partial \Omega )$.

5.2. Simple points, multiple points, and inverses

[Definition: Multiple point] Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic and not constant. Then $P\in \Omega $ is a multiple point of $f$ if the function $g(z)=f(z)-f(P)$ has a zero of multiplicity at least $2$ at $P$. If $f(P)=Q$ and $g$ has a zero of multiplicity $k$, we say that $f(P)=Q$ with order $k$.

[Definition: Simple point] Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic and not constant. Then $P\in \Omega $ is a simple point of $f$ if it is not a multiple point of $f$, that is, if the function $g(z)=f(z)-f(P)$ has a zero of multiplicity $1$ at $P$. If $f(P)=Q$, we say that $f(P)=Q$ with order $1$.

Theorem 5.2.2. Let $\Omega \subseteq \C $ be open and connected and let $f:\Omega \to \C $ be holomorphic and not constant. Let $P\in \Omega $ and let $Q=f(P)$ with order $k$.

Then there exists a $\delta >0$ and a $\varepsilon >0$ such that if $w\in D(Q,\varepsilon )\setminus \{Q\}$ then there are exactly $k$ points $z_1,\dots ,z_k\in D(P,\delta )$ such that $f(z_j)=w$. Furthermore, each $z_j$ is a simple point.

(Problem 3070) In this problem we begin the proof of Theorem 5.2.2. Show that if $P\in \Omega $, then there is a $\rho >0$ such that there are no multiple points in $D(P,\rho )\setminus \{P\}\subset \Omega $. Hint: Start by showing that $P$ is a multiple point of $f$ if and only if $f'(P)=0$.

(Problem 3090) Let $R>0$ be such that $z=P$ is the only solution in $D(P,R)$ to $f(z)=f(P)$. Such an $R$ must exist by Problem 2050. Let $\rho $ be as in Problem 3070, and let $0<\delta <\min (R,\rho )$. Let $U$ be the connected component of $\C \setminus f(\partial D(P,\delta ))$ containing $Q$; recall from Problem 3010 that $U$ is open. Suppose that $w\in U\setminus \{Q\}$. Show that there are exactly $k$ points $z_1,\dots ,z_k\in D(P,\delta )\setminus \{P\}$ with $f(z_j)=w$.

(Problem 3110) Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be holomorphic. Let $P\in \Omega $ and suppose that $f'(P)\neq 0$. Show that there is a $r>0$ with $D(P,r)\subseteq \Omega $ and such that $f$ is one-to-one on $D(P,r)$.

(Problem 3111) Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be holomorphic. Let $P\in \Omega $ and suppose that $f(P)=0$. Show that there does not exist a $r>0$ with $D(P,r)\subseteq \Omega $ and such that $f$ is one-to-one on $D(P,r)$.

(Problem 3120) Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C $ be holomorphic and one-to-one. Let $W=f(\Omega )$. Show that $f^{-1}:W\to \Omega $ is continuous.

[Chapter 5, Problem 7] Let $\Omega $ be open and connected and let $f:\Omega \to \C $ be holomorphic and injective. Then $f^{-1}:f(\Omega )\to \Omega $ is also holomorphic.

5.3. Further Results on the Zeros of Holomorphic Functions: Rouché’s theorem

Theorem 5.3.1. [Rouché’s theorem.] Let $\Omega \subseteq \C $ be open. Let $f:\Omega \to \C $ and $g:\Omega \to \C $ be holomorphic. Suppose that $\overline D(P,r)\subseteq \Omega $ and that

\begin{equation*}|f(z)-g(z)|\neq |f(z)|+|g(z)|\end{equation*}

for all $z\in \partial D(P,r)$. Then $f$ and $g$ have the same number of zeroes (counted with multiplicities) in $D(P,r)$.

(Problem 3130) In this problem we show an example of an application of Rouché’s theorem. The polynomial $p(z)=z^{7}+4z^2+2$ has seven zeroes (with multiplicity). Use Rouché’s theorem to determine how many of these zeroes are in the disc $D(0,1)$.

(Problem 3140) The polynomial $p(z)=z^{7}+3z^2+2$ has seven zeroes (with multiplicity). Use Rouché’s theorem to determine how many of these zeroes are in the disc $D(0,1)$.

(Problem 3150) In this problem we begin the proof of Rouché’s theorem. Let $\eta $, $\phi :[0,1]\to \C $ be two $C^1$ closed curves. Suppose that

\begin{equation*}|\eta (t)-\phi (t)|\neq |\eta (t)|+|\phi (t)|\end{equation*}

for all $0\leq t\leq 1$. Show that $\eta $ and $\phi $ are homotopic in $\C \setminus \{0\}$.

Recall [Problem 2540]: Suppose that $\phi $ and $\eta $ are homotopic closed curves in $\Omega \setminus \{P\}$. Then $\Ind _{\phi }(P)=\Ind _{\eta }(P)$.

Recall [Problem 2970]: Suppose that $\gamma $ is the standard counterclockwise parameterization of $\partial D(P,r)$, that $f$ is holomorphic in $D(P,R)$ for some $R>r$, and that $f(\partial D(P,r))\subset \C \setminus \{0\}$. Then $\Ind _{f\circ \gamma }(0)$ is equal to the number of solutions to $f(z)=0$ in $D(P,r)$ (counted with multiplicity).

5.4. The Maximum Modulus Principle

Theorem 5.4.2. (The maximum modulus principle.) Let $\Omega \subseteq \C $ be a connected open set and let $f:\Omega \to \C $ be holomorphic. Suppose that there is a $w\in \Omega $ such that $|f(w)|\geq |f(z)|$ for all $z\in \Omega $. Then $f$ is constant.

(Problem 3170) Prove the maximum modulus principle. Hint: Show that $f(\Omega )$ is not open.

Theorem 5.4.4. (The maximum modulus principle, sharpened.) Let $\Omega \subseteq \C $ be a connected open set and let $f:\Omega \to \C $ be holomorphic. Suppose that there is a $r>0$ and a $w\in \Omega $ such that $D(w,r)\subseteq \Omega $ and such that $|f(w)|\geq |f(z)|$ for all $z\in D(w,r)$. Then $f$ is constant.

Corollary 5.4.3. (The maximum modulus theorem.) Let $\Omega \subseteq \C $ be a bounded open set. Let $f:\overline \Omega \to \C $ be continuous on $\overline \Omega $ and holomorphic on $\Omega $. Then there is a $w\in \partial \Omega $ such that $|f(w)|\geq |f(z)|$ for all $z\in \overline \Omega $.

(Problem 3200) Give an example of an unbounded connected open set $\Omega $ with nonempty boundary and a continuous function $f:\overline \Omega \to \C $ such that $f$ is holomorphic in $\Omega $ and such that $|f(w)|<\sup _{z\in \overline \Omega } |f(z)|$ for all $w\in \overline \Omega $. Bonus: Can you give an example in which $f$ is bounded in $\Omega $ and another example in which $f$ is bounded on $\partial \Omega $ but unbounded in $\Omega $?

Proposition 5.4.5. (The minimum modulus principle.) Let $\Omega \subseteq \C $ be a connected open set and let $f:\Omega \to \C $ be holomorphic. Suppose that there is a $w\in \Omega $ such that $|f(w)|\leq |f(z)|$ for all $z\in \Omega $. Then either $f$ is constant or…

(Problem 3210) Finish the statement of Proposition 5.4.5 and prove that your claim is correct.

5.3. Further Results on the Zeros of Holomorphic Functions: Hurwitz’s theorem

Theorem 5.3.3. [Hurwitz’s theorem.] Let $\Omega \subseteq \C $ be a connected open set. If $k\in \N $, let $f_k:\Omega \to \C \setminus \{0\}$ be a nowhere zero holomorphic function. Suppose that $f_k\to f$, uniformly on compact subsets of $\Omega $. Suppose that $f(w)\neq 0$ for at least one $w\in \Omega $. Then $f(z)\neq 0$ for all $z\in \Omega $.

(Problem 3220) Give an example of a connected open set $\Omega \subseteq \C $ and a sequence of holomorphic functions $f_k:\Omega \to \C \setminus \{0\}$ such that $f_k(z)\neq 0$ for all $z\in \Omega $ and all $k\in \N $ but such that $f_k\to 0$ uniformly on all compact subsets of $\Omega $.

(Problem 3231) Let $\Omega \subseteq \C $ be a connected open set. If $k\in \N $, let $f_k:\Omega \to \C \setminus \{0\}$ be an injective holomorphic function. Suppose that $f_k\to f$, uniformly on compact subsets of $\Omega $. Show that $f$ is either constant or injective.

5.5. The Schwarz Lemma

Theorem 5.5.1. (Schwarz’s lemma.) Let $f:\D \to \C $ be a function such that

then there is a $\theta \in \R $ such that $f(z)=ze^{i\theta }$ for all $z\in \D $.

(Problem 3240) Let $f:\D \to \D $ be holomorphic with $f(0)=0$. Begin the proof of Schwarz’s lemma by proving that $|f'(0)|\leq 1$ and that $|f(z)|\leq |z|$ for all $z\in \D $.

(Problem 3250) Complete the proof of Schwarz’s lemma. That is, suppose that in addition either $|f(z)|=|z|$ for some $z\in \D $ or $|f'(0)|=1$. Show that there is a $\theta \in \R $ such that $f(z)=ze^{i\theta }$ for all $z\in \D $.

5.5. Möbius transformations

Then $\phi _c$ is a holomorphic bijection from $\D $ to itself, a continuous bijection from $\partial \D $ to itself, and a continuous bijection from $\overline \D $ to itself.

(Problem 3270) In this problem we begin the proof of Lemma 3260. Show that $\phi _c$ is holomorphic on $\D $ and continuous on $\overline \D $.

(Problem 3280) Show that $\phi _c(\D )\subseteq \D $ and that $\phi _c(\partial \D )\subseteq \partial \D $.

(Problem 3290) Show that $\phi _c(\phi _{-c}(z))=z$ for all $z\in \overline \D $.

(Problem 3300) Show that $\phi _c(\D )=\D $ and that $\phi _c(\partial \D )=\partial \D $. This completes the proof of Lemma 3260.

(Problem 3310) We will now establish some further properties of $\phi _c$. Show that

(Problem 3320) If $\theta \in \R $, show that $\phi _c(e^{i\theta }z) = e^{i\theta } \phi _{ce^{-i\theta }}(z)$.

(Problem 3330) If $c$, $w\in \D $, show that $\phi _c\circ \phi _w=e^{i\theta }\phi _b$ for some $b\in \D $ and some $\theta \in \R $.

(Problem 3331) Let $G=\{\phi _c:c\in \D \}\cup \{f:f(z)=ze^{i\theta }$ for some $\theta \in \R \}$. Show that $G$ is a group (with function composition as the group action) and is a subgroup of the group of all holomorphic bijections from $\D $ to itself.

5.5. The Schwarz-Pick lemma

(Problem 3340) Let $f:\D \to \D $ be holomorphic. Let $a\in \D $ and let $b=f(a)$. Let $g=\phi _b\circ f\circ \phi _{-a}$. Show that $g$ satisfies the conditions of Schwarz’s lemma (Theorem 5.5.1).

(Problem 3350) Apply Schwarz’s lemma to $g$ to derive an upper bound on $|f'(a)|$.

(Problem 3360) Let $w\in \D \setminus \{a\}$. What does Schwarz’s lemma tell you about $f(a)$ and $f(w)$?

Theorem 5.5.2. [The Schwarz-Pick lemma.] Let $f:\D \to \C $ be a function such that

If a nontrivial equality holds (either $|f'(a)|=\frac {1-|f(a)|^2}{1-|z|^2}$ for some $a\in \D $, or $\left |\frac {f(a)-f(w)}{1-\overline {f(a)}f(w)}\right | = \left |\frac {a-w}{1-\overline {a}w}\right |$ for some $a$, $w\in \D $ with $a\neq w$), then there is a $\theta \in \R $ and a $c\in \D $ such that

\begin{equation*}f(z)= e^{i\theta } \frac {z-c}{1-\overline {c}z}\end{equation*}

6.3. Linear Fractional Transformations

Definition 6.3.1. We say that a function $f:\C \cup \{\infty \}\to \C \cup \{\infty \}$ is a fractional linear transformation if there exist numbers $a$, $b$, $c$, $d\in \C $ such that $ad-bc\neq 0$ and such that

\begin{equation*}f(z)=\begin {cases} \frac {az+b}{cz+d}, & z\in \C \text { and either }c=0\text { or }z\neq -d/c,\\ \infty , & z=-d/c,\>c\neq 0,\\ \infty , & z=\infty , \> c=0,\\ \frac {a}{c}, &z=\infty ,\> c\neq 0. \end {cases} \end{equation*}

Theorem 6.3.4. Let $a$, $b$, $c$, and $d\in \C $ with $ad-bc\neq 0$. Let $f$ be the fractional linear transformation given in Definition 6.3.1.

Then $f$ is continuous as a function from $\C \cup \{\infty \}$ to itself if we use the metric in Problem 2780.

Furthermore, $f$ is a bijection from $\C \cup \{\infty \}$ to itself and its inverse is a fractional linear transformation.

Finally, if $g$ is another fractional linear transformation then so is $f\circ g$.

(Problem 3362) Begin the proof of Theorem 6.3.4 by showing that $f$ is continuous as a function from $\C \cup \{\infty \}$ to itself if we use the metric in Problem 2780. Furthermore, show that $f$ is the only continuous function from $\C \cup \{\infty \}$ to itself that also satisfies $f(z)=\frac {az+b}{cz+d}$ for all $z\in \C $ such that $cz+d\neq 0$.

(Problem 3370) Continue the proof of Theorem 6.3.4 by showing that $f$ is a bijection from $\C \cup \{\infty \}$ to itself and that its inverse is a fractional linear transformation.

(Problem 3380) Complete the proof of Theorem 6.3.4 by showing that the composition of two fractional linear transformations is a fractional linear transformation.

More precisely, let $f$ and $g$ be two fractional linear transformations and let $a$, $b$, $c$, $d$, $\alpha $, $\beta $, $\gamma $, $\delta $ be the complex numbers such that

\[f(z)=\frac {az+b}{cz+d}\text { if } z\in \C ,\>cz+d\neq 0, \quad g(z)=\frac {\alpha z+\beta }{\gamma z+\delta }\text { if } z\in \C ,\>\gamma z+\delta \neq 0.\]

Let $\zeta $, $\eta $, $\theta $, $\kappa $ be the complex numbers that satisfy

\[\begin {pmatrix}\zeta& \eta \\\theta& \kappa \end {pmatrix} =\begin {pmatrix}a&b\\c&d\end {pmatrix} \begin {pmatrix}\alpha& \beta \\\gamma& \delta \end {pmatrix} .\]

Show that $\zeta \kappa -\eta \theta \neq 0$ and that, if $h$ is the fractional linear transformation such that

If there are real numbers $a$, $b$, and $r>0$ such that $S=\{x+iy:x\in \R ,\>y\in \R ,\> (x-a)^2+(y-b)^2=r^2\}$, then we say that $S$ is a circle. (Observe that circles by definition have positive radius.)

If there are real numbers $a$, $b$, and $c$, with $a$ and $b$ not both zero, such that $S=\{\infty \}\cup \{x+iy:x\in \R ,\>y\in \R ,\>ax+by=c\}$, then we say that $S$ is a line. (Observe that lines include the point at $\infty $ and circles do not.)

Theorem 6.3.7. Let $f$ be a fractional linear transformation and let $S\subset \C \cup \{\infty \}$. If $S$ is a circle, then $f(S)$ is either a line or a circle, and if $S$ is a line, then $f(S)$ is either a line or a circle.

(Problem 3390) Suppose that $ad-bc\neq 0$. Show that if $az+b=0$ then $cz+d\neq 0$.

(Problem 3400) In this problem we begin the proof of Theorem 6.3.7. Specifically, we begin by examining the preimages of the particular circle $\partial \D $ under fractional linear transformations. Let $f$ be a fractional linear transformation. Let $S=\{z\in \C \cup \{\infty \}:|f(z)|=1\}$. Show that $S\cap \C $ and $\C \setminus S$ both contain infinitely many points.

(Problem 3410) Let $f$ be a fractional linear transformation and let $a$, $b$, $c$, $d$ be such that $f(z)=\frac {az+b}{cz+d}$ whenever $cz+d\neq 0$. Let $S=\{z\in \C \cup \{\infty \}:|f(z)|=1\}$. Show that there exist real numbers $\alpha $ and $\beta $ such that

(Problem 3420) If $|a|=|c|$, show that $S$ is a line (recall this means that $\infty \in S$).

(Problem 3430) If $|a|\neq |c|$, show that $S$ is a circle (of positive radius).

(Problem 3440) Let $S\subset \C \cup \{\infty \}$ be either a straight line or a circle of positive radius. Show that there is a fractional linear transformation such that $S=\{z\in \C \cup \{\infty \}:|f(z)|=1\}=f^{-1}(\partial \D )$.

(Problem 3450) Complete the proof of Theorem 6.3.7 by showing that if $f$ is any fractional linear transformation and $S$ is either a line or a circle, then $f(S)$ is also either a line or a circle.

(Problem 3460) Let $f(z)=\frac {z+1}{iz-i}$. Show that $f(\D )=\H $, where $\H =\{x+iy:x\in \R , y\in (0,\infty )\}$.

(Problem 3470) Let $f(z)=\frac {z-1}{iz+i}$. Show that $f(\{z\in \C :|z|<1,\>\im z>0\})=\{x+iy:x,y\in (0,\infty )\}$.

6. Holomorphic functions as Geometric Mappings

(Problem 3480) Find a holomorphic bijection $f$ from the quarter-plane $\{x+iy:x,y\in (0,\infty )\}$ to the upper half-plane $\H $.

(Problem 3490) Find a holomorphic bijection from the strip $\{x+iy:x\in \R ,\>y\in (0,\pi )\}$ to the upper half plane.

(Problem 3500) Find a holomorphic bijection from $\D \setminus \{0\}$ to $\C \setminus \overline \D $.

(Problem 3510) Find a holomorphic bijection from $\D $ to the strip $\{x+iy:x\in \R ,\>y\in (0,\pi )\}$.

(Problem 3520) Find a holomorphic bijection from the quarter-circle $\{z\in \C :|z|<1,\>\re z>0,\>\im z>0\}$ to the upper half plane.

6.1. Biholomorphic self-maps of $\C $

[Definition: Biholomorphic self-map] Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \Omega $. We say that $f$ is a biholomorphic self-map if it is holomorphic in $\Omega $ and is a bijection from $\Omega $ to $\Omega $.

Theorem 6.1.1. Let $f:\C \to \C $. Then $f$ is a biholomorphic self-map if and only if there are complex numbers $a$, $b\in \C $ with $a\neq 0$ such that that $f(z)=az+b$ for all $z\in \C $.

(Problem 3560) In this problem we prove the more straightforward direction of Theorem 6.1.1. Let $a$, $b\in \C $ with $a\neq 0$. Show that $f(z)=az+b$ is a biholomorphic self-map of $\C $.

(Problem 3570) Let $f:\C \to \C $ be a biholomorphic self-map. Show that $\lim _{z\to \infty } |f(z)|=\infty $.

(Problem 3580) Let $f:\C \to \C $ be a biholomorphic self-map. Given that $f$ has a pole at $\infty $ and no singularity at $0$, what can you say about the Laurent series for $f$ in $\C \setminus \{0\}$?

(Problem 3590) Let $f:\C \to \C $ be a biholomorphic self-map. Show that $f(z)=az+b$ for some $b\in \C $ and some $a\in \C \setminus \{0\}$.

[Chapter 6, Problem 2] Suppose that $f:\C \to \C $ is holomorphic and one-to-one. Then $f$ is linear (and, in particular, is also surjective).

6.2. Real analysis

(Problem 3600) Let $X$ and $Z$ be two topological spaces and let $f:X\to Z$ be a continuous bijection with continuous inverse. Let $Y\subseteq X$. Show that $f(\partial Y)=\partial f(Y)$.

6.2. Biholomorphic self-maps of $\D $

(Problem 3610) Let $f:\D \to \D $ be a biholomorphic self-map. Show that $f(z)=e^{i\theta } \frac {z-c}{1-\overline c z}$ for some $c\in \D $ and some $\theta \in \R $. Hint: Let $g=f^{-1}$. Compute $|g'(f(0)) \,f'(0)|$ and use the Schwarz-Pick lemma.

[Chapter 1, Problem 10] A fractional linear transformation $f(z)=\frac {az+b}{cz+d}$ is a bijection from $\H $ to itself if and only if $a$, $b$, $c$, and $d$ are real numbers and $ad-bc>0$.

(Problem 3620) Let $f:\H \to \H $ be a biholomorphic self-map. Show that $f$ is a fractional linear transformation (and therefore must be as in Problem 1.10).

(Problem 3621) function. Show that $f$ is a biholomorphic self-map if and only if $f(z)=\frac {az+b}{cz+d}$ for some real numbers $a$, $b$, $c$, and $d$ that satisfy $ad-bc>0$. Hint: Most of the work consists in showing that $f$ is a fractional linear transformation.

6.3. Bimeromorphic self-maps of $\C \cup \{\infty \}$

(Problem 3630) We have seen that fractional linear transformations are bimeromorphic self-maps of $\C \cup \{\infty \}$. Conversely, let $f:\C \cup \{\infty \}\to \C \cup \{\infty \}$ be a meromorphic bijection (with $f(z)=\infty $ if $f$ has a pole at $z$; because $f$ is a bijection it has a single pole). Show that $f$ is a fractional linear transformation. Hint: Does it suffice to prove this in the case that $f(\infty )=\infty $?

6.4. The Riemann Mapping Theorem

(Problem 3640) Let $\Omega \subseteq \C $ be open and simply connected. Let $f:\Omega \to \C $ be holomorphic. Show that there exists a holomorphic function $F:\Omega \to \C $ such that $F'=f$.

[Definition: Holomorphically simply connected] A connected open set $\Omega \subset \C $ is holomorphically simply connected if, whenever $f:\Omega \to \C $ is holomorphic, there exists a holomorphic function $F:\Omega \to \C $ with $F'=f$.

(Bonus Problem 3650) Let $\Omega \subseteq \C $ be open and holomorphically simply connected. Show that $\Omega $ is simply connected.

Theorem 6.4.2. [The Riemann mapping theorem.] Suppose that $\Omega \subsetneq \C $ is a holomorphically simply connected open set; we emphasize $\Omega \neq \C $. Then there exists a conformal mapping (holomorphic bijection) $f:\Omega \to \D $.

Furthermore, for any $a\in \Omega $, there exists a unique conformal mapping $f:\Omega \to \D $ such that $f(a)=0$ and such that $f'(a)$ is a positive real number.

(Problem 3660) Assume the Riemann mapping theorem is true. Prove that every holomorphically simply connected region is simply connected.

(Problem 3670) We now begin the proof of Theorem 6.4.2. Suppose that $\varphi :\D \to \D $ is a conformal mapping, that $\varphi (0)=0$, and that $\varphi '(0)>0$ (that is, $\varphi '(0)$ is a positive real number). Prove that $\varphi $ is the identity.

(Problem 3680) Let $\Omega \subset \C $ be a connected open set and let $a\in \Omega $. Prove that there is at most one function $f:\Omega \to \D $ that satisfies the conditions of the Riemman mapping theorem.

Lemma 6.6.4. If $\Omega $ is holomorphically simply connected, $f$ is holomorphic on $\Omega $, and $f\neq 0$ on $\Omega $, then there is some holomorphic function $h$ on $\Omega $ such that $e^h=f$.

(Problem 3700) Let $\Omega =\C \setminus \{x+0i:x\leq 0\}$ be the complex plane minus a slit. Let $f(z)=z^2$ be holomorphic on $\Omega $.

Corollary 6.6.5. If $\Omega $ is holomorphically simply connected, $f$ is holomorphic on $\Omega $, and $f\neq 0$ on $\Omega $, then there is some holomorphic function $k$ on $\Omega $ such that $k^2=f$.

(Problem 3720) Suppose that $\Omega \subset \C $ is open and that for some $Q\in \C $ and $r>0$, we have that $\Omega \cap D(Q,r)=\emptyset $. Find a one-to-one holomorphic function $g:\Omega \to \D $. ($g$ need not be a bijection.)

(Problem 3730) Suppose that $\Omega $ is holomorphically simply connected and that $P\notin \Omega $ for some $P\in \C $. Using the function $h$ of Problem 3690, show that there exists a one-to-one holomorphic function $g:\Omega \to \D $. [This problem will be assigned as homework. Note that your book does this exercise using the function $k$ of Problem 3710.]

(Problem 3740) Let $\Omega \subsetneq \C $ be holomorphically simply connected with $a\in \Omega $. Let $\mathcal {F}$ be the set of all functions $f$ such that

To prove the Riemann mapping theorem, what do we need to prove about $\mathcal {F}$?

(Problem 3760) Let $R=\sup \{f'(a):f\in \mathcal {F}\}$. Show that $0<R<\infty $.

Claim 6.7.3. If $f\in \mathcal {F}$ and $f'(a)=R$, then $f:\Omega \to \D $ is surjective.

(Problem 3770) Let $0<r<1$. Let $W=\D \setminus (-1,-r]=\{x+iy:x^2+y^2<1$ and either $y\neq 0$ or $x>-r\}$ be the unit disc with a slit removed; then $0\in W\subsetneq \D $. Let

\begin{equation*}\psi (z)=\phi _{\sqrt r}(\sqrt {\phi _{-r}(z)})\end{equation*}

where $\phi _c$ is as in Lemma 3260 and where $\sqrt {re^{i\theta }}=\sqrt {r}e^{i\theta /2}$ if $0<r<\infty $ and $-\pi <\theta <\pi $. Show that

Note: You must prove $\psi '(0)>1$; this is much harder than proving $\psi '(0)>0$!

(Problem 3780) Let $W\subsetneq \D $ be open and holomorphically simply connected with $0\in W$. Show that there exists a $\psi $ such that

Hint: The construction will be similar to the previous problem with Corollary 6.6.5 in place of the explicit square root function. Note: You must prove $\psi '(0)>1$; this is much harder than proving $\psi '(0)>0$!

(Problem 3790) Let $\Omega \subseteq \C $ be open and holomorphically simply connected and let $f:\Omega \to \C $ be a holomorphic injection. Show that $f(\Omega )$ is also open and holomorphically simply connected.

(Problem 3800) Prove Claim 6.7.3 by showing that if $f\in \mathcal {F}$ is not surjective, then there is a $g\in \mathcal {F}$ such that $f'(a)<g'(a)$.

6.5. Real Analysis

(Problem 3810) State the Bolzano-Weierstraß theorem in $\R ^p$. What does this tell you about bounded sequences in $\C $?

(Problem 3820) Show that every sequence in a compact set has a convergent subsequence.

[Definition: Equicontinuous] Let $\{f_n\}_{n=1}^\infty $ be a sequence of functions from $(X,d)$ to $(Y,\varrho )$, where $(X,d)$ and $(Y,\varrho )$ are two metric spaces. Suppose that for each $x\in X$ and each $\varepsilon >0$ there is a $\delta =\delta _{\varepsilon ,x}>0$ such that if $y\in X$ with $d(x,y)<\delta _{\varepsilon ,x}$ then $\sup _{n\in \N } \varrho (f_n(x),f_n(y))<\varepsilon $ (that is, $\varrho (f_n(x),f_n(y))<\varepsilon $ for all $n\in \N $, and $\delta _{\varepsilon ,x}$ cannot depend on $n$.) Then we say that the sequence $\{f_n\}_{n=1}^\infty $ is equicontinuous.

If $\delta =\delta _\varepsilon $ may be taken to be independent of $x$, then the sequence is uniformly equicontinuous.

(Bonus Problem 3821) Suppose that $\{f_n\}_{n=1}^\infty $ is an equicontinuous sequence of functions and that their common domain $(X,d)$ is compact. Show that $\{f_n\}_{n=1}^\infty $ is uniformly equicontinuous.

(Problem 3822) Give an example of a bounded sequence in a complete metric space that does not have a convergent subsequence.

6.5. Normal Families

Definition 6.5.1. If $\{f_j\}_{j=1}^\infty $ is a sequence of functions from an open set $\Omega \subseteq \C $ to $\C $, we say that $\{f_j\}_{j=1}^\infty $ converges normally to $f$ if $\{f_j\}_{j=1}^\infty $ converges to $f$ uniformly on compact subsets $K$ of $\Omega $.

If $\mathcal {F}$ is a family of functions such that $f:\Omega \to \C $ for each $f\in \mathcal {F}$, and if every sequence in $\mathcal {F}$ has a subsequence that converges normally, we say that $\mathcal {F}$ is a normal family.

Recall [Problem 1900]: If each $f_j$ is holomorphic and $f_j\to f$ normally then $f$ is holomorphic.

Recall [Problem 1920]: If each $f_j$ is holomorphic and $f_j\to f$ normally then $f_j'\to f'$ normally.

Theorem 6.5.3. [Montel’s theorem, first version.] Suppose that $\mathcal {F}$ is a family of functions that are holomorphic on some open set $\Omega $. Suppose that there is a constant $M>0$ such that, if $f\in {\mathcal {F}}$ and $z\in \Omega $, then $\abs {f(z)}\leq M$. Then $\mathcal {F}$ is a normal family.

The Arzelà-Ascoli Theorem. Let $(\Psi ,d)$ and $(Y,\rho )$ be compact metric spaces.3 Let $\{f_n\}_{n=1}^\infty $ be an equicontinuous sequence of functions from $X$ to $Y$. Then there is a subsequence $\{f_{n_k}\}_{k=1}^\infty $ of $\{f_n\}_{n=1}^\infty $ that converges uniformly on $\Psi $.

(Problem 3830) In this problem we begin the proof of the Arzelà-Ascoli theorem. This problem is a strengthening of the known fact that compact sets are separable. Suppose that $\Psi $ is compact and that for each positive number $\varepsilon >0$ and each $z\in \Psi $ we are given a positive number $\delta _{\varepsilon ,z}>0$. Show that there exists a sequence $\{z_m\}_{m=1}^\infty \subset \Psi $ such that, for each $\varepsilon >0$, there is a $M\in \N $ such that $\Psi \subseteq \bigcup _{m=1}^M B(z_m,\min (\varepsilon ,\delta _{\varepsilon ,z_m}))$.

(Problem 3840) Let $\Psi $, $Y$, and $f_n$ be as in the Arzelà-Ascoli theorem. Let $\{z_m\}_{m=1}^\infty \subseteq \Psi $ be a sequence. Show that there is one subsequence $\{f_{n_k}\}_{k=1}^\infty $ of $\{f_n\}_{n=1}^\infty $ (with $n_k$ independent of $m$) such that $\{f_{n_k}(z_m)\}_{k=1}^\infty $ is a convergent sequence for each $m\in \N $.

(Problem 3850) Suppose in addition that $z_m$ is as in Problem 3830. Show that $\{f_{n_k}\}_{k=1}^\infty $ is uniformly convergent on $\{z_m:m\in \N \}$.

(Problem 3860) Prove the Arzelà-Ascoli theorem by showing that $\{f_{n_k}\}_{k=1}^\infty $ is uniformly convergent on $\Psi $.

(Problem 3870) In this problem we begin the proof of Montel’s theorem. Let $\{f_j\}_{j=1}^\infty $ be a sequence of holomorphic functions defined on an open set $\Omega \subset \C $. Suppose that there is a $M\in \R $ such that $|f_j(z)|\leq M$ for all $z\in \Omega $ and $j\in \N $. Let $\Psi \subset \Omega $ be compact. Show that the functions $f_j$ satisfy the conditions of the Arzelà-Ascoli theorem on $\Psi $.

(Problem 3880) Show that if $\Omega \subset \C $ is open, then there exist compact sets $\Psi _1\subset \Psi _2\subset \Psi _3\subset \dots $ such that $\cup _m \Psi _m=\Omega $ and such that every compact set $K\subset \Omega $ is contained in $\Psi _m$ for some $m\in \N $. (This property is called $\sigma $-compactness.)

6.7. The Proof of the Analytic Form of the Riemann Mapping Theorem

Recall [Problem 3740]: Let $\Omega \subsetneq \C $ be holomorphically simply connected with $a\in \Omega $. Let $\mathcal {F}$ be the set of all functions $f$ such that

Recall [Problem 3800]: (Claim 6.7.3.) If $f\in \mathcal {F}$ and $f'(a)=\sup \{g'(a):g\in \mathcal {F}\}$, then $f:\Omega \to \D $ is onto.

(Problem 3900) Prove that there is a function $f\in \mathcal {F}$ with $f'(a)=\sup \{g'(a):g\in \mathcal {F}\}$. (This proves the Riemann mapping theorem.)

7.1. Basic Properties of Harmonic Functions

Definition 7.1.1. Harmonic function. We say that $u$ is harmonic in a domain $\Omega \subseteq \C $ if $u$ is $C^2$ in $\Omega $ and if $\frac {\partial ^2 u}{\partial x^2}+\frac {\partial ^2 u}{\partial y^2}=0$ in $\Omega $.

(Problem 3910) Let $\Omega \subseteq \C $ be open and let $u\in C^2(\Omega )$. Show that $u$ is harmonic if and only if $\frac {\partial }{\partial z} \left (\frac {\partial u}{\partial \overline z}\right )=0$ and also that $u$ is harmonic if and only if $\frac {\partial }{\partial \overline z} \left (\frac {\partial u}{\partial z}\right )=0$.

(Problem 3911) Suppose that $\Omega \subseteq \C $ is open and that $u$, $v:\Omega \to \C $ are both harmonic. Let $\alpha $, $\beta \in \C $. Show that $\alpha u+\beta v$ is also harmonic.

[Chapter 7, Problem 12] If $u$ is a real-valued harmonic function on a connected open set, and if $u^2$ is also harmonic, then $u$ is a constant.

[Chapter 7, Problem 13] If $u$ is a complex-valued harmonic function on a connected open set $\Omega $, and if $u^2$ is also harmonic, then $u$ is either holomorphic or conjugate-holomorphic (meaning that either $u$ or $\overline u$ is holomorphic, or, equivalently, either $\p [u]{z}\equiv 0$ or $\p [u]{\overline z}\equiv 0$ in $\Omega $).

(Problem 3920) Prove that if $F$ is holomorphic in an open set $\Omega $ and $u=\re F$ then $u$ is harmonic.

Lemma 7.1.4. If $u$ is real-valued and harmonic in a simply connected open set $\Omega $, then there is a holomorphic function $f$ such that $\re f=u$.

Corollary 7.1.3. If $\Omega \subseteq \C $ is open and $u:\Omega \to \R $ is harmonic, then $u$ is smooth.

[Definition: Harmonic conjugate] Let $u$ and $v$ be two real-valued functions. If $F=u+iv$ is holomorphic, then we say that $v$ is a harmonic conjugate of $u$.

[Chapter 7, Problem 4] Suppose that $v_1$ and $v_2$ are both conjugates of the (real harmonic) function $u$. What can you say about $v_1$ and $v_2$?

(Problem 3941) Let $u$ be a harmonic function. Suppose that $v$ is a harmonic conjugate of $u$. Is $u$ also a harmonic conjugate of $v$?

7.2. The Maximum Principle

Theorem 7.2.1. (The maximum principle for harmonic functions.) If $\Omega \subseteq \C $ is open and connected, if $u:\Omega \to \R $ is harmonic, and if there is a $P\in \Omega $ such that $u(P)\geq u(z)$ for all $z\in \Omega $, then $u$ is constant in $\Omega $.

(Problem 3960) State and prove the minimum principle and corollaries involving the values of $u$ on $\partial \Omega $.

7.2. The Mean Value Property

Theorem 7.2.5. (The mean value property.) If $u$ is harmonic in a neighborhood of $\overline D(P,r)$, then

\begin{equation*}u(P)=\frac {1}{2\pi } \int _0^{2\pi } u(P+re^{i\theta })\,d\theta .\end{equation*}

(Problem 3980) Suppose that $u$ is harmonic in $D(P,r)$ and continuous on $\overline D(P,r)$ (without necessarily being harmonic in any larger set). Is the mean value property still valid?

7.3. The Poisson Integral Formula

Lemma 7.3.2. Let $\Omega $, $W\subseteq \C $ be open sets, let $\psi :\Omega \to W$ be holomorphic, and let $u:W\to \R $ be harmonic. Then $u\circ \psi $ is harmonic.

[Definition: Poisson integral kernel] Let $P(z,\zeta )=\frac {\abs {\zeta }^2-\abs {z}^2}{2\pi \abs {\zeta -z}^2}$; $P$ is called the Poisson kernel.

Theorem 7.3.3. (The Poisson integral formula.) Suppose that $u$ is harmonic in $D(0,R)\supset \overline \D $ for some $R>1$. If $z\in \D $, then

\begin{align*} u(w)&=\int _0^{2\pi } u(e^{i\psi })\,P(w,e^{i\psi })\,d\psi = \frac {1}{2\pi }\int _0^{2\pi } u(e^{i\psi })\,\frac {1-\abs {w}^2}{\abs {e^{i\psi }-w}^2}\,d\psi . \end{align*}

Recall [Problem 1340]: Let $\Omega \subseteq \C $ be open and let $\overline D(P,r)\subset \Omega $. Let $f$ be holomorphic in $\Omega $. Then $f(z)=\frac {1}{2\pi i}\oint _\gamma \frac {f(\zeta )}{\zeta -z}\,d\zeta $ for all $z\in D(P,r)$.

Recall [Problem 1460]: Let $f$ be continuous on $\partial D(P,r)$. Define $F$ by $F(z)=\frac {1}{2\pi i}\oint _{\partial D(P,r)} \frac {f(\zeta )}{\zeta -z}\,d\zeta $ for all $z\in D(P,r)$. Then $F$ is $C^1$ and holomorphic in $D(P,r)$.

[Chapter 2, Problem 21] It is not necessarily true that $\lim _{w\to z} F(w)=f(z)$ for $z\in \partial D(P,r)$.

Theorem 7.3.4. Let $f:\partial \D \to \R $ be continuous. If $z\in \D $, define

\begin{equation*}u(z)= \int _0^{2\pi } f(e^{i\psi })\,P(z,e^{i\psi })\,d\psi =\frac {1}{2\pi }\int _0^{2\pi } f(e^{i\psi })\,\frac {1-\abs {z}^2}{\abs {e^{i\psi }-z}^2}\,d\psi .\end{equation*}

Then $u$ is harmonic in $\D $, and $\lim _{z\to e^{i\theta }} u(z)=f(e^{i\theta })$ for all $\theta \in [0,2\pi ]$. In particular, if we define $u(z)=f(z)$ for all $z\in \partial \D $, then $u$ is continuous on $\overline \D $.

(Problem 4010) Let $P_r(\theta )=\frac {1}{2\pi }\frac {1-r^2}{{1-2r\cos (\theta )+r^2}}$. Show that $P_r(\theta -\psi )=P(re^{i\theta },e^{i\psi })$, so that

\begin{align*} v(re^{i\theta })&=\frac {1}{2\pi }\int _0^{2\pi } v(e^{i\psi })\,P_r(\theta -\psi )\,d\psi \end{align*}

for all $0\leq r<1$, all $\theta \in \R $ and all $v:\overline \D \to \R $ continuous and harmonic in $\D $.

(Problem 4020) Prove that if $\theta $ is real and $0\leq r<1$ then $0<P_r(\theta )<\infty $ (in particular, the denominator is never zero).

(Problem 4030) Show that $p(z)=P(z,\zeta )$ is harmonic on $\C \setminus \{\zeta \}$; in particular, if $\zeta =e^{i\theta }$ then $p(z)$ is harmonic in $\D $.

(Problem 4050) Prove that if $0\leq r<1$ then $\int _0^{2\pi } P_r(\theta )\,d\theta =1$.

(Problem 4060) Prove that $\lim _{r\to 1^-} P_r(\theta )=0$ for all $\theta \neq 2n\pi $.

(Problem 4070) Let $0<\delta <\pi $ be a small positive number. Prove that $\smash {\lim _{r\to 1^-} P_r(\theta )=0}$ uniformly for all $\delta <\theta <2\pi -\delta $.

(Problem 4080) Let $0<\delta <\pi $. Prove that $\lim _{r\to 1^-} \int _{-\delta }^\delta P_r(\theta )\,d\theta =1$.

(Problem 4090) Let $u$, $f$ be as in Theorem 7.3.4. Show that $u(re^{i\theta })$ converges to $f(e^{i\theta })$ as $r\to 1^-$ uniformly in $\theta $.

(Problem 4100) Let $u$, $f$ be as in Theorem 7.3.4. Show that $u$ is continuous on $\overline \D $. (This completes the proof of Theorem 7.3.4. This differs from the previous problem in that the previous problem considers $u(z)$ as $z\to e^{i\theta }$ along a ray through the origin, while this problem considers $u(z)$ as $z\to e^{i\theta }$ along arbitrary paths.)

(Problem 4110) Write an analogue to Theorem 7.3.4 in an arbitrary disc. That is, let $P\in \C $, $r>0$, and $f:\partial D(P,r)\to \R $ be continuous. Show that there is a function $u$ that is harmonic in $D(P,r)$, continuous on $\overline D(P,r)$, and satisfies $u(z)=f(z)$ for all $z\in \partial D(P,r)$. Can you write a formula for $u$ in $D(P,r)$?

(Problem 4111) Show that Theorem 7.3.3 is valid if $u$ is merely harmonic in $\D $ and continuous on $\overline D$ (rather than being harmonic in an open superset of $\overline D$). Also, write and prove an analogue in an arbitrary disc. That is, if $u$ is harmonic in $D(P,r)$ and continuous on $\overline D(P,r)$, write a formula for $u$ in $D(P,r)$ in terms of $u$ on $\partial D(P,r)$.

[Chapter 7, Problem 25] If $u$ is harmonic in $\H =\{x+iy:x\in \R ,\>y>0\}$ and continuous on $\overline \H $, and if $\lim _{|z|\to \infty } u(z)$ exists (and is finite), then

Conversely, if $f:\R \to \R $ is continuous, if $\lim _{t\to \infty } f(t)=\lim _{t\to -\infty } f(t)\in \R $, and if we define

\[u(x+iy)=\begin {cases} \frac {1}{\pi }\int _{-\infty }^\infty f(t)\frac {y}{(x-t)^2+y^2}\,dt, & y>0,\\ f(x), & y=0,\end {cases}\]

(Problem 4112) Suppose that $f:\R \to \R $ is bounded and continuous. However, we do not require that $\lim _{t\to \infty } f(t)$ or $\lim _{t\to -\infty } f(t)$ exist. Show that if

\[u(x+iy)=\begin {cases} \frac {1}{\pi }\int _{-\infty }^\infty f(t)\frac {y}{(x-t)^2+y^2}\,dt, & y>0,\\ f(x), & y=0,\end {cases}\]

then we still have that $u$ is harmonic in $\H =\{x+iy:x\in \R ,\>y>0\}$ and continuous on $\overline \H $.

(Problem 4113) Suppose that $u$ and $v$ are harmonic in some open set $\Omega $, that $\overline D(P,r)\subset \Omega $, and that $u(z)=v(z)$ for all $z\in \partial D(P,r)$. Show that $u(z)=v(z)$ for all $z\in D(P,r)$.

[Chapter 7, Problem 22] If $u$ is harmonic in a connected open set $\Omega $ and $u=0$ in $D(P,r)$ for some $D(P,r)\subseteq \Omega $ with $r>0$, then $u=0$ everywhere in $\Omega $.

(Problem 4114) Give an example of two harmonic functions that are equal on a set with an accumulation point but are not equal everywhere.

(Problem 4115) Show that the zeroes of a real harmonic function cannot be isolated. That is, let $\Omega \subseteq \C $ be open and let $u:\Omega \to \R $ be harmonic. Let $P\in \Omega $ with $u(P)=0$ and let $r>0$. Show that $u(z)=0$ for some $z\in D(P,r)\setminus \{P\}$.

7.4. Real Analysis

(Problem 4120) Let $a<b$ and let $f:[a,b]\to \R $ be a nonnegative continuous function that satisfies $\int _a^b f=0$. Show that $f(x)=0$ for all $x\in [a,b]$.

7.4. Regularity of Harmonic Functions

Definition 7.4.1. Let $\Omega \subset \C $ be open and let $h:\Omega \to \R $ be continuous. We say that $h$ has the small circle mean value property (SCMV property) if, for every $P\in \Omega $, there is some number $\varepsilon _P>0$ such that $D(P,\varepsilon _P)\subset \Omega $ and such that $h(P)=\frac {1}{2\pi }\int _0^{2\pi } h(P+\varepsilon e^{i\theta })\,d\theta $ for all $0<\varepsilon <\varepsilon _P$.

Recall [Theorem 7.2.5]: If $u$ is harmonic in an open set $\Omega $, then $u$ has the small circle mean value property, and if $P\in \Omega $ then $\varepsilon _P$ is the largest number such that $D(P,\varepsilon _P)\subseteq \Omega $.

Lemma 7.4.4. Let $\Omega \subset \C $ be open and connected. Let $g$ be continuous on $\Omega $ and satisfy the “small circle” mean value property. Suppose furthermore that there is some $P\in \Omega $ such that $g(P)\geq g(z)$ for all $z\in \Omega $. Then $g$ is constant.

(Problem 4140) Suppose that $g$ is continuous on $\overline D(P,r)$ and has the “small circle” mean value property in $D(P,r)$. Suppose further that $g=0$ on $\partial D(P,r)$. Show that $g=0$ in $D(P,r)$.

(Problem 4150) Suppose that $g$ and $h$ are continuous on $\overline D(P,r)$ and that $g=h$ on $\partial D(P,r)$. Suppose that $h$ is harmonic in $D(P,r)$ and that $g$ has the “small circle” mean value property in $D(P,r)$. Show that $g=h$ in $D(P,r)$ as well.

Theorem 7.4.2. Let $\Omega \subset \C $ be open. Suppose that $g:\Omega \to \R $ is continuous and has the “small circle” mean value property in $\Omega $. Then $g$ is harmonic in $\Omega $.

Corollary 7.4.3. Let $\Omega \subset \C $ be open. Suppose that $\{h_j\}_{j=1}^\infty $ is a sequence of functions, each harmonic on $\Omega $, and that $h_j\to h$ uniformly on compact subsets of $\Omega $. Then $h$ is also harmonic.

(Problem 4170) Prove Corollary 7.4.3. Hint: Show that $h$ has the “small circle” mean value property.

7.5. The Schwarz Reflection Principle

Lemma 7.5.1. Let $\Psi \subset \C $ be open and connected. Suppose that $\Psi $ is symmetric about the real axis; that is, $z\in \Psi $ if and only if $\overline z\in \Psi $. Let $\Omega =\{z\in \Psi :\im z>0\}$.

Let $v:\overline \Omega \cap \Psi \to \R $ be continuous. Suppose that $v$ is harmonic in $\Omega $ and that $v(x)=0$ for all $x\in \partial \Omega \cap \Psi =\R \cap \Psi $.

Then there is a function $\widehat v:\Psi \to \R $ that is harmonic in $\Psi $ and satisfies $\widehat v=v$ in $\Omega $. Furthermore,

\begin{equation*}\widehat v(z)=\begin {cases} v(z), & z\in \Omega ,\cr 0, & z\in \partial \Omega \cap \Psi , \cr \noalign {\vskip 1pt} -v(\overline z), & z\in \widehat \Omega =\{w\in \C :\overline w\in \Omega \}.\end {cases}\end{equation*}

Sketch $\Psi $. Label $\Omega $, $\widehat \Omega $, the set where $v$ is harmonic, and the set where $v$ is equal to zero.

(Problem 4190) Suppose $\Omega \subset \C $ is open and that $v$ is harmonic on $\Omega $. Let $w(z)={v(\overline z)}$. Show that $w$ is harmonic on $\widehat \Omega =\{z\in \C :\overline z\in \Omega \}$.

(Problem 4200) Let $\Psi $, $\Omega $, $\widehat \Omega $, $v$, and $\widehat v$ be as in Lemma 7.5.1. Show that $\widehat v$ is continuous in $\Psi $.

(Problem 4210) Suppose that $v$, $\widehat v$, and $\Psi $ are as in Lemma 7.5.1. Show that $\widehat v$ is harmonic in $\Psi $. This completes the proof of Lemma 7.5.1.

[Chapter 7, Problem 1] Liouville’s theorem is true for harmonic functions: if $u:\C \to \C $ is both bounded and harmonic, then $u$ is constant.

(Problem 4211) If $u$ is harmonic in $\H =\{x+iy:x\in \R ,\>y>0\}$ and continuous on $\overline \H $, and in addition is bounded, show that

Theorem 7.5.2. Let $\Psi $ and $\Omega $ be as in Lemma 7.5.1. That is, let $\Psi \subset \C $ be open, connected, and symmetric about the real axis. Let $\Omega =\{z\in \Psi :\im z>0\}$.

Let $f:\overline \Omega \cap \Psi \to \R $ be continuous. Suppose that $f$ is holomorphic in $\Omega $ and that $\im f(x)=0$ for all $x\in \partial \Omega \cap \Psi $.

Then there is a function $\widehat f:\Psi \to \R $ that is holomorphic in $\Psi $ and satisfies $\widehat f=f$ in $\Omega $. Furthermore,

\begin{equation*}\widehat f(z)=\begin {cases} f(z), & z\in \overline \Omega \cap \Psi ,\cr \overline { f(\overline z)}, & z\in \widehat \Omega =\{w\in \C :\overline w\in \Omega \}.\end {cases}\end{equation*}

(Problem 4220) Suppose $\Omega \subset \C $ is open and that $f$ is holomorphic on $\Omega $. Let $g(z)=\overline {f(\overline z)}$. Show that $g$ is holomorphic on $\widehat \Omega =\{z\in \C :\overline z\in \Omega \}$.

(Problem 4230) Suppose that $f$ is holomorphic in $D(x_0,r)$ for some $x_0\in \R $ and some $r>0$. Suppose further that $f(x)$ is real for all $x\in (x_0-r,x_0+r)=D(x_0,r)\cap \R $. Show that $f(z)=\overline {f(\overline {z})}$ for all $z\in D(x_0,r)$.

(Problem 4240) Prove Theorem 7.5.2. Hint: Start with the special case where $\Psi $ is a disc centered at a point on the real axis.

(Problem 4250) Suppose that $f$ is holomorphic on $\H =\{z\in \C :\im z>0\}$ and continuous on $\overline \H $ and that $f(x)=0$ for all $0<x<1$. Show that $f(z)=0$ for all $z\in \H $.

7.6. Real Analysis

(Memory 4260) Let $\{x_j\}_{j=1}^\infty $ be an increasing sequence of real numbers, that is, $x_j\in \R $ and $x_j\leq x_{j+1}$ for all $j\in \N $. Show that either $x_j\to \infty $ or $x_j\to x$ for some $x\in \R $.

Recall [Problem 1590]: If $E$ is a set, $(X,d)$ is a complete metric space, $f_k:E\to X$, and $\{f_k\}_{k=1}^\infty $ is uniformly Cauchy, then $\{f_k\}_{k=1}^\infty $ converges uniformly to some $f:E\to X$.

7.6. Harnack’s Principle

(Problem 4270) Recall that if $u$ is harmonic in $D(P,R)$ and continuous on $\overline D(P,R)$, then for any $0\leq r<R$ and any $0\leq \theta \leq 2\pi $,

\begin{equation*}u(P+re^{i\theta })=\frac {1}{2\pi } \int _0^{2\pi } u(P+Re^{i\psi })\frac {R^2-r^2}{\abs {Re^{i\psi }-re^{i\theta }}^2}\,d\psi .\end{equation*}

\begin{equation*}\min _{0\leq \theta \leq 2\pi ,0\leq \psi \leq 2\pi }\frac {R^2-r^2}{\abs {Re^{i\psi }-re^{i\theta }}^2} =\frac {R-r}{R+r}\end{equation*}

\begin{equation*}\max _{0\leq \theta \leq 2\pi ,0\leq \psi \leq 2\pi }\frac {R^2-r^2}{\abs {Re^{i\psi }-re^{i\theta }}^2}=\frac {R+r}{R-r}.\end{equation*}

Corollary 7.6.2. (The Harnack inequality.) Suppose that $u$ is nonnegative and harmonic in $ D(P,R)$ and continuous on $\overline D(P,R)$. If $z\in D(P,R)$ with $r=|z-P|$, then

\begin{equation*}\frac {R-r}{R+r} u(P)\leq u(z)\leq \frac {R+r}{R-r} u(P).\end{equation*}

(Problem 4290) Did we need the assumption that $u$ was continuous on $\overline D(P,R)$?

Theorem 7.6.3. (Harnack’s principle.) Let $\{u_k\}_{k=1}^\infty $ be a sequence of real-valued functions harmonic in a connected open set $\Omega \subseteq \C $ such that $u_1(z)\leq u_2(z)\leq u_3(z)\leq \cdots $ for each $z\in \Omega $. Then either $u_k\to \infty $ uniformly on compact sets or there is a function $u:\Omega \to \R $ such that $u_k\to u$ uniformly on compact sets.

(Problem 4300) In this problem we begin the proof of Theorem 7.6.3. Let $\Omega $ and $u_k$ be as in Theorem 7.6.3. Let $D(P,R)\subseteq \Omega $. Suppose that $\smash {\lim _{j\to \infty } u_k(P)=\infty }$. Show that $u_k\to \infty $ uniformly on $\overline D(P,r)$ for any $0<r<R$.

(Problem 4310) Suppose that $\lim _{k\to \infty } u_k(P)<\infty $. Show that $\{u_k\}_{k=1}^\infty $ converges to some (finite) harmonic function, uniformly on $D(P,r)$ for any $0<r<R$.

(Problem 4320) Show that either $\lim _{k\to \infty } u_k(z)=\infty $ for all $z\in \Omega $ or $\lim _{k\to \infty } u_k(z)<\infty $ for all $z\in \Omega $.

7.7. Real Analysis

(Problem 4331) Suppose that $u$ and $v$ are both real-valued and continuous in a set $\Omega $. Let $f(z)=\max (u(z),v(z))$. Show that $f$ is continuous in $\Omega $.

7.7. Subharmonic Functions

[Definition: Subharmonic functions] Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \R $ be continuous. Suppose that for every $\overline D(P,r)\subset \Omega $, we have that

\begin{equation*}f(P)\leq \frac {1}{2\pi } \int _0^{2\pi } f(P+re^{i\theta })\,d\theta .\end{equation*}

[Definition: Superharmonic functions] Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \R $ be continuous. Suppose that for every $\overline D(P,r)\subset \Omega $, we have that

\begin{equation*}f(P)\geq \frac {1}{2\pi } \int _0^{2\pi } f(P+re^{i\theta })\,d\theta .\end{equation*}

(Problem 4340) Show that $f$ is subharmonic if and only if $-f$ is superharmonic.

(Problem 4350) Suppose that $f$ is a continuous, real-valued function in an open set $\Omega \subseteq \C $. Show that $f$ is harmonic if and only if $f$ is both subharmonic and superharmonic.

(Problem 4360) Suppose that $f$ is subharmonic in an open set $\Omega $ and that $\alpha \neq 0$ is a nonzero real number. Show that $\alpha f$ is subharmonic if $\alpha >0$ and that $\alpha f$ is superharmonic if $\alpha <0$.

(Problem 4370) Suppose that $f$ and $g$ are both subharmonic in an open set $\Omega $. Show that $f+g$ is subharmonic in $\Omega $. Is $f-g$ subharmonic in $\Omega $?

(Problem 4380) Suppose that $f$ is subharmonic and $g$ is superharmonic in an open set $\Omega \subseteq \C $. Show that $f-g$ is subharmonic in $\Omega $.

(Problem 4390) Suppose that $u$ and $v$ are both subharmonic in an open set $\Omega $. Let $f(z)=\max (u(z),v(z))$. Show that $f$ is subharmonic in $\Omega $. (In particular, if $u$ and $v$ are real and harmonic then $f$ is subharmonic.)

(Problem 4400) Let $\Omega \subset \C $ be open and let $f:\Omega \to \C $ be holomorphic. Show that $u(z)=\abs {f(z)}$ is subharmonic in $\Omega $.

(Problem 4410) Let $\Omega \subset \C $ be open and let $u:\Omega \to \C $ be subharmonic. Let $\varphi :\R \to \R $ be nondecreasing and convex, so that if $0<t<1$ and $a$, $b\in \R $ then $\varphi (ta+(1-t)b)\leq t\varphi (a)+(1-t)\varphi (b)$. Show that $v(z)=\varphi (u(z))$ is subharmonic in $\Omega $.

[Chapter 7, Problem 46] If $u$ is harmonic and $\varphi $ is convex, then $\varphi \circ u$ is subharmonic even if $\varphi $ is not nondecreasing.

(Problem 4420) Give an example of a function that is subharmonic in a domain $\Omega $ but is not harmonic in that domain.

Proposition 7.7.7. Subharmonic functions satisfy the maximum principle. That is, suppose that $\Omega \subseteq \C $ is open and connected, that $f:\Omega \to \R $ is subharmonic, and that there is a $P\in \Omega $ such that $f(P)\geq f(z)$ for all $z\in \Omega $. Then $f$ is constant in $\Omega $.

(Problem 4450) Prove the following generalization of Proposition 7.7.7. Let $\Omega \subseteq \C $ be open and connected. Suppose that $f:\Omega \to \R $ is continuous and satisfies the small circle sub-mean-value property: for every $P\in \Omega $, there is some $\varepsilon _P>0$ such that $D(P,\varepsilon _P)\subset \Omega $ and such that

\begin{equation*}f(P)\leq \frac {1}{2\pi } \int _0^{2\pi } f(P+\varepsilon e^{i\theta })\,d\theta \quad \hbox {for all $0<\varepsilon <\varepsilon _P$}.\end{equation*}

Proposition 7.7.4. Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \R $ be continuous. Then $f$ is subharmonic (in the sense given in these lecture notes) if and only if, whenever $\overline D(P,r)\subset \Omega $, $h$ is harmonic in $D(P,r)$ and continuous on $\overline D(P,r)$, and $h\geq f$ on $\partial D(P,r)$, we have that $h\geq f$ in $D(P,r)$.

(Problem 4470) Begin the proof of Proposition 7.7.4 as follows. Suppose that $\Omega \subseteq \C $ is open and that $f:\Omega \to \R $ is continuous. Suppose further that whenever $\overline D(P,r)\subset \Omega $, $h$ is harmonic in $D(P,r)$ and continuous on $\overline D(P,r)$, and $h\geq f$ on $\partial D(P,r)$, we have that $h\geq f$ in $D(P,r)$. Prove that $f$ is subharmonic in the sense that $f$ satisfies the sub-mean-value property

(Problem 4480) Complete the proof of Proposition 7.7.4 and strengthen the result as follows. Let $\Omega \subseteq \C $ be open. Suppose that $f:\Omega \to \R $ is continuous and satisfies the small circle sub-mean-value property in $\Omega $ (as in Problem 4450). Show that whenever $\overline D(P,r)\subset \Omega $, $h$ is harmonic in $D(P,r)$ and continuous on $\overline D(P,r)$, and $h\geq f$ on $\partial D(P,r)$, we have that $h\geq f$ in $D(P,r)$.

7.7. The Dirichlet Problem

[Definition: The Dirichlet problem] Let $\Omega \subsetneq \C $ be a nonempty connected open set. We say that the Dirichlet problem is well posed on $\Omega $ if, for every function $f$ defined and continuous on $\partial \Omega $, there is exactly one function $u$ that is harmonic in $\Omega $, continuous on $\overline \Omega $, and such that $u=f$ on $\partial \Omega $.

(Problem 4490) Give an example of an unbounded domain $\Omega $ and two distinct functions $u$ and $v$ that are harmonic in $\Omega $, continuous on $\overline \Omega $ and equal zero on $\partial \Omega $.

(Problem 4500) Prove that we have uniqueness for the Dirichlet problem in any bounded domain; that is, show that if $\Omega \subsetneq \C $ is bounded, if $u$ and $v$ are both harmonic in $\Omega $ and continuous on $\overline \Omega $, and if $u=v$ on $\partial \Omega $, then $u=v$ in $\Omega $. Clearly explain how you used the fact that $\Omega $ is bounded.

(Problem 4510) Let $0<r<1$. Let $u(z)=\frac {1}{\log r}\log |z|$. Show that $u$ is harmonic in the annulus $\Omega =D(0,1)\setminus D(0,r)$, continuous on $\overline \Omega $, and satisfies $u(e^{i\theta })=0$, $u(re^{i\theta })=1$ for any $0\leq \theta \leq 2\pi $.

(Problem 4530) Let $\Omega =D(0,1)\setminus \{0\}$. Suppose that $u$ is harmonic in $\Omega $, continuous on $\overline \Omega $, and that $u=0$ on $\partial D(0,1)$. Prove that $u(0)=0$. Is the Dirichlet problem well posed in $\Omega $?

Definition 7.7.8. Let $\Omega \subsetneq \C $ be open and let $P\in \partial \Omega $. Suppose that the function $b:\overline \Omega \to \R $ has the following properties.

Theorem 7.8.1. Let $\Omega \subset \C $ be a nonempty bounded connected open set. The Dirichlet problem is well posed in $\Omega $ if and only if, for every $P\in \partial \Omega $, there is a function $b_P$ that is a barrier for $\Omega $ at $P$.

(Problem 4540) If $b$ is a barrier for $\Omega $ at $P$, show that $b(z)<0$ for all $z\in \Omega $.

Example 7.7.10. Let $\Omega \subsetneq \C $ be a nonempty bounded open set. Let $P\in \partial \Omega $ satisfy $|P|\geq |z|$ for all $z\in \overline \Omega $. Then the function $b(z)=\re (\frac {1}{P}z)-1$ is a barrier for $\Omega $ at $P$.

Example 7.7.12. Suppose that $\Omega \subsetneq \C $ is open and $P\in \partial \Omega $. Suppose that there is an $r>0$ such that there exists a barrier $b_1$ for $\Omega \cap D(P,r)$ at $P$. If $\varepsilon >0$ is small enough, then the function

\[b_2(z)=\begin {cases}-\varepsilon& \text {if }z\in \overline \Omega \setminus D(P,r),\\ \max (-\varepsilon ,b_1(z))&\text {if } z\in \overline \Omega \cap D(P,r)\end {cases}\]

(Problem 4550) Prove that the function $b_2$ in Example 7.7.12 is indeed a barrier for $\Omega $ at $P$.

(Problem 4570) Show that there is a barrier for the domain $\Omega =\C \setminus [0,\infty )=\{re^{i\theta }:r>0,\> 0<\theta <2\pi \}$ at the point $P=0$.

Example 7.7.11. If $\Omega \subsetneq \C $ is an open set, $P\in \partial \Omega $, and $\C \setminus \Omega $ contains a line segment with one end point at $P$, then there exists a barrier for $\Omega $ at $P$.

(Problem 4580) Show that the barrier of Example 7.7.11 exists. You don’t have to give an explicit formula for the barrier.

(Problem 4590) Let $\Omega =\D \setminus \{0\}$. Show that there is no barrier for $\Omega $ at $0$. Hint: Suppose that $b$ satisfies all of the properties of a barrier except that $b(0)\leq 0$ instead of $b(0)=0$. Show that $b$ may be bounded above by a suitable modification of the harmonic function in Problem 4510 and see what you can conclude about $b$.

7.8. Real Analysis

(Memory 4600) Let $(X,d)$ and $(Y,\varrho )$ be metric spaces. Suppose that $X=F\cup D$, where $F$ and $D$ are (relatively) closed. Let $f:X\to Y$ be a function. Suppose that $f\big \vert _F$ and $f\big \vert _D$ are both continuous. Then $f$ is continuous.

7.8. The Perròn Method and the Solution of the Dirichlet Problem

Recall [Theorem 7.8.1]: Let $\Omega \subset \C $ be a nonempty bounded connected open set. The Dirichlet problem is well posed in $\Omega $ if and only if, for every $P\in \partial \Omega $, there is a function $b_P$ that is a barrier for $\Omega $ at $P$.

(Problem 4610) Prove the “only if” direction of Theorem 7.8.1: Suppose that the Dirichlet problem is well posed in $\Omega $ and $P\in \partial \Omega $ and construct a barrier for $\Omega $ at $P$.

(Problem 4620) Let $\Omega \subset \C $ be a nonempty bounded connected open set and let $f:\partial \Omega \to \R $ be continuous. Let $M=\max _{\partial \Omega } |f|$. Let

\[S=\{\psi \in C^0(\overline \Omega ):\text {$\psi $ is subharmonic in~$\Omega $ and satisfies $\psi \leq f$ on~$\partial \Omega $}\}\]

where $C^0(\overline \Omega )$ is the set of all continuous functions on $\overline \Omega $. Then:

Then $-M\leq u(z)\leq M$ (and $u(z)$ exists) for all $z\in \overline \Omega $. Show that $u(P)\leq f(P)$ for all $P\in \partial \Omega $.

(Problem 4640) Let $P\in \partial \Omega $ and let $b_P$ be a barrier for $\Omega $ at $P$. Let $\varepsilon >0$. Show that there exists a $C>0$ large enough that

(Problem 4650) Let $P\in \partial \Omega $ and let $\varepsilon >0$. Show that there is a $\delta >0$ such that if $|z-P|<\delta $ and $z\in \overline \Omega $ then $u(z)>f(P)-\varepsilon $. (This implies in particular that $u(P)=f(P)$ but also implies that $u$ is lower semicontinuous at $P$.)

(Problem 4660) Show that $u$ is continuous at $P$ for all $P\in \partial \Omega $.

(Problem 4670) Let $\psi \in S$ and let $\overline D(P,r)\subset \Omega $. Define

\[\varphi (w)=\begin {cases} \psi (w), & w\notin D(P,r),\\ \frac {1}{2\pi } \int _0^{2\pi } \psi (P+re^{i\theta }) \frac {r^2-|w-P|^2}{|P+re^{i\theta }-w|^2}\,d\theta , &w\in D(P,r).\end {cases}\]

Show that $\varphi $ is also in $S$ and that $\varphi (\zeta )\geq \psi (\zeta )$ for all $\zeta \in \overline \Omega $.

(Problem 4680) Let $\overline D(P,r)\subset \Omega $ for some $r>0$. For each $w\in D(P,r)$, show that there is a sequence of functions $\{\varphi _{w,n}\}_{n=1}^\infty $, all of which are in $S$, harmonic in $D(P,r)$, and nondecreasing on $\Omega $, such that $u(w)=\lim _{n\to \infty } \varphi _{w,n}(w)$.

(Problem 4690) For each $w$, $z\in D(P,r)$, show that there is a sequence of functions $\{\varphi _{w,z,n}\}_{n=1}^\infty $, all of which are in $S$, harmonic in $D(P,r)$, and nondecreasing on $\Omega $, such that $u(w)=\lim _{n\to \infty } \varphi _{w,z,n}(w)$, $u(z)=\lim _{n\to \infty } \varphi _{w,z,n}(z)$, and if $\zeta \in \Omega $ then $\varphi _{z,w}(\zeta )\geq \varphi _z(\zeta )$ and $\varphi _{z,w}(\zeta )\geq \varphi _w(\zeta )$.

Recall [Theorem 7.6.3]: (Harnack’s principle.) Let $\{u_k\}_{k=1}^\infty $ be a sequence of real-valued functions harmonic in a connected open set $\Omega \subseteq \C $ such that $u_1(z)\leq u_2(z)\leq u_3(z)\leq \cdots $ for each $z\in \Omega $. Then either $u_k\to \infty $ uniformly on compact sets or there is a harmonic function $u:\Omega \to \R $ such that $u_k\to u$ uniformly on compact sets.

\[u_w(\zeta )=\lim _{n\to \infty } \varphi _{w,n}(\zeta ), \qquad u_{z,w}(\zeta )=\lim _{n\to \infty } \varphi _{z,w,n}(\zeta ).\]

Then $u_w$ and $u_{z,w}$ are both harmonic in $D(P,r)$. Show that $u_w(\zeta )=u_{z,w}(\zeta )$ for all $\zeta \in D(P,r)$.

7.9. Real Analysis

(Memory 4720) (The Bolzano-Weierstraß theorem.) Suppose that $\{z_n\}_{n=1}^\infty \subset \R ^d$ is bounded. Then there is a subsequence $\{z_{n_k}\}_{k=1}^\infty $ that converges as $k\to \infty $.

7.9. Conformal Mappings of Annuli

Theorem 7.9.1. Let $0<r_1<R_1<\infty $ and $0<r_2<R_2<\infty $. Let $P_1\in \C $ and $P_2\in \C $. Let $A_1=\{z\in \C :r_1<\abs {z-P_1}<R_1\}$ and $A_2=\{z\in \C :r_2<\abs {z-P_2}<R_2\}$. Then $A_1$ and $A_2$ are conformally equivalent (meaning that there is a holomorphic bijection $\varphi :A_1\to A_2$) if and only if $R_1/r_1=R_2/r_2$.

[Chapter 7, Problem 37] Let $A=\{z\in \C : 1/R<\abs {z}<R\}$ be an annulus for some $R>1$. Find all conformal self-maps of $A$.

(Problem 4730) Prove the straightforward direction of Theorem 7.9.1; that is, assume $R_1/r_1=R_2/r_2$ and prove that $A_1$ and $A_2$ are conformally equivalent.

(Problem 4740) Suppose that Theorem 7.9.1 is true in the special case where and $P_1=P_2=0$. Show that Theorem 7.9.1 is true for any $P_1$, $P_2\in \C $.

(Problem 4750) Suppose that there exists some $\varphi :A_1\to A_2$ that is a holomorphic bijection. Let $z_\infty \in \partial A_1$. Let $\{z_n\}_{n=1}^\infty \subset A_1$ with $z_n\to z_\infty $. Then $\{\varphi (z_n)\}_{n=1}^\infty \subset A_2$ is bounded, so by the Bolzano-Weierstraß theorem there is a subsequence $\{z_{n_k}\}_{k=1}^\infty $ such that $\varphi (z_{n_k})$ converges. Show that $\varphi (z_{n_k})$ converges to a point in $\partial A_2$. Hint: You only need that $\varphi $ and $\varphi ^{-1}$ are continuous, not that they are holomorphic.

for some $0<r_1<R_1<\infty $, $0<r_2<R_2<\infty $. Suppose that $\varphi :A_1\to A_2$ is a holomorphic bijection.

Let $\{z_n\}_{n=1}^\infty \subset A_1$ and $\{\zeta _m\}_{m=1}^\infty \subset A_1$ with

By passing to subsequences, we may assume that $\{\varphi (z_n)\}_{n=1}^\infty $ and $\{\varphi (\zeta _m)\}_{m=1}^\infty $ also converge. By Problem 4750,

\begin{gather*} \text {either }|\varphi (z_{n})|\to R_2\text { or }|\varphi (z_{n})|\to r_2, \\ \text {either }|\varphi (\zeta _m)|\to R_2\text { or }|\varphi (\zeta _m)|\to r_2. \end{gather*}

(Problem 4770) We now begin the proof of Lemma 4760a. Let $r_2<\rho <R_2$. Let $s_\rho =\sup \{\abs {\varphi ^{-1}(\rho e^{i\theta })}:0\leq \theta \leq 2\pi \}$. Show that $r_1< s_\rho <R_1$.

(Problem 4780) Let $r_2<\rho <R_2$. Let $\Omega _{\rho }^-=\{z\in A_1:|\varphi (z)|<\rho \}$ and let $\Omega _{\rho }^+=\{z\in A_1:|\varphi (z)|>\rho \}$. Show that $\Omega _\rho ^+$ and $\Omega _\rho ^-$ are disjoint connected open sets.

(Problem 4790) Suppose that $|\varphi (z_{n})|\to R_2$. Show that $\abs {\varphi (z)}>\rho $ for all $z\in A_1$ with $\abs {z}>s_\rho $.

(Problem 4800) Suppose that $|\varphi (z_{n})|\to R_2$. Show that $\lim _{z\to w} |\varphi (z)|=R_2$ for all $w\in \partial D(0,R_1)$.

(Problem 4820) Let $\Omega \subseteq \C $ be open and let $f:\Omega \to \C \setminus \{0\}$ be holomorphic. Show that $u(z)=\log |f(z)|$ is harmonic in $\Omega $. (Note that $\Omega $ may not be simply connected, and so Lemma 6.6.4 cannot be applied in $\Omega $.)

(Problem 4830) Let $A_1$, $A_2$, and $\varphi $ be as in Lemma 4760. Let $u(z)=\log |\varphi (z)|$ for all $z\in A_1$, $u(z)=\lim _{\zeta \to z}|\varphi (\zeta )|$ for all $z\in \partial A_1$. Then $u$ is continuous on $\overline {A_1}$ and harmonic in $A_1$. Show that there exist constants $\alpha $ and $\beta $ such that

(Problem 4840) Let $\Omega =A_1\setminus (-\infty ,0)$ be the annulus with the negative real numbers deleted. Then the function $\log $ can be defined such that it is holomorphic on $\Omega $. Show that there is a $\omega \in \C $ such that $\varphi (z)=\omega e^{\beta \log z}$ for all $z\in \Omega $, where $\beta $ is as in the previous problem.

(Problem 4850) Given that $\varphi $ is continuous on $A_1$ (and so continuous up to the negative reals), what must be true about the number $\beta $? Given that $\varphi $ is injective on $A_1$ (and in particular on $\{e^{i\theta }:-\pi <\theta \leq \pi \}$), what must be true about the number $\beta $?

[Chapter 6, Problem 31] If $f$ is a fractional linear transformation, $c$ and $C$ are concentric circles, and $f(c)$ and $f(C)$ are also concentric circles, then the ratio of the radii of $c$ and $C$ is equal to the ratio of the radii of $f(c)$ and $f(C)$.

8.1. Basic Concepts Concerning Infinite Sums and Products

[Chapter 8, Problem 2] Let $\{A_k\}_{k=1}^\infty $ be a sequence of complex numbers. Suppose $A_k\neq 0$ for all $k$ and that $\lim _{N\to \infty }\prod _{k=1}^N A_k$ exists and is a finite nonzero complex number. Show that $\lim _{k\to \infty } A_k=1$.

(Problem 4870) Do we still have that $\lim _{k\to \infty } A_k=1$ if we allow $\lim _{N\to \infty }\prod _{k=1}^N A_k$ to equal zero? Do we still have that $\lim _{k\to \infty } A_k=1$ if we allow $A_k$ to equal zero for some $k$?

Definition 8.1.1. Let $\{a_n\}_{n=1}^\infty \subset \C $ be a sequence of complex numbers. We say that the infinite product

\begin{equation*}\prod _{n=1}^\infty (1+a_n)\end{equation*}

\begin{equation*}\lim _{N\to \infty } \prod _{n=N_0}^N (1+a_n) \in \C \setminus \{0\}.\end{equation*}

(Problem 4880) Show that if $\prod _{n=1}^\infty (1+a_n)$ converges, then $(1+a_n)\neq 0$ for all but finitely many $n$, and $a_n\to 0$.

Corollary 8.1.3. If $\{a_k\}_{k=1}^n\subset \C $ with $\abs {a_k}<1$ for each $1\leq k\leq n$, then $\exp \Bigl (\frac {1}{2}\sum _{k=1}^n \abs {a_k}\Bigr ) \leq \prod _{k=1}^n (1+\abs {a_k}) \leq \exp \Bigl (\sum _{k=1}^n \abs {a_k}\Bigr )$.

(Problem 4910) Suppose that $\{a_k\}_{k=1}^\infty \subset \C $. Show that either $\prod _{k=1}^\infty (1+|a_k|)$ converges to a positive real number or $\lim _{N\to \infty }\prod _{k=1}^N (1+|a_k|)=\infty $.

Corollary 8.1.4. If $\{a_k\}_{k=1}^\infty \subset \C $ with $\sum _{k=1}^\infty |a_k|<\infty $, then $\prod _{k=1}^\infty (1+|a_k|)$ converges.

Corollary 8.1.5. If $\{a_k\}_{k=1}^\infty \subset \C $ and $\prod _{k=1}^\infty (1+|a_k|)$ converges, then $\sum _{k=1}^\infty |a_k|<\infty $.

Theorem 8.1.7. If $\prod _{k=1}^\infty (1+|a_k|)$ converges, then $\prod _{k=1}^\infty (1+a_k)$ converges.

(Problem 4940) (This is the first step in the proof of Theorem 8.1.7.) Let $\{a_k\}_{k=1}^\infty \subset \C $. Show that if $N\geq M\geq 1$, then

\begin{equation*}{\biggl |\biggl (\prod _{k=M}^N (1+a_k)\biggr )-1\biggr | \leq \biggl (\prod _{k=M}^N (1+\abs {a_k})\biggr )-1}.\end{equation*}

(Problem 4950) Show that if $\prod _{k=1}^\infty (1+|a_k|)$ converges, then there is a $N_0$ such that if $n\geq N_0$ then $1+a_n\neq 0$.

(Problem 4960) Show that if $\prod _{k=1}^\infty (1+|a_k|)$ converges and $N_0$ is as in the previous problem, then

\begin{equation*}\Bigl \{\prod _{k=N_0}^N (1+a_k)\Bigr \}_{N=N_0}^\infty \end{equation*}

(Problem 4970) Show that if $\prod _{k=1}^\infty (1+|a_k|)$ converges and $N_0$ is as in the previous problem, then

\begin{equation*}\inf _{N\geq N_0} \Bigl |\prod _{k=N_0}^N (1+a_k)\Bigr |>0\end{equation*}

and so $\prod _{k=N_0}^N (1+a_k)$ does not converge to zero. This completes the proof of Theorem 8.1.7.

Corollary 8.1.8. If $\sum _{k=1}^\infty |a_k|$ converges, then $\prod _{k=1}^\infty (1+a_k)$ converges. (This follows immediately from Corollary 8.1.5 and Theorem 8.1.7, so you may use the result at once.)

[Definition: Notation for multiplicity] If $\Omega \subseteq \C $ is open, $f:\Omega \to \C $ is holomorphic, $z\in \Omega $, and $f$ is not identically zero in the connected component of $\Omega $ containing $z$, then we let $\mathop {\mathrm {mult}}\nolimits _f(z)$ be the multiplicity of the zero of $f$ at $z$. For convenience, if $f(z)\neq 0$ we take $\mult _f(z)=0$.

Theorem 8.1.9. Let $\Omega \subseteq \C $ be open. Let $f_n:\Omega \to \C $ be holomorphic. Suppose that

\begin{equation*}\sum _{n=1}^\infty |f_n|\end{equation*}

(Problem 4980) Let $f_n$ and $\Omega $ be as in Theorem 8.1.9. Show that if $K\subset \Omega $ is compact then $\sup \{|f_n(z)|:n\in \N ,\>z\in K\}$ is finite (that is, that the functions $\{f_n:n\in \N \}$ are uniformly bounded on $K$).

(Problem 4990) (This is the first step of the proof of Theorem 8.1.9.) Let $f_n$ and $\Omega $ be as in Theorem 8.1.9 and let $K\subset \Omega $ be compact. By Corollary 8.1.8, if $z\in K$ then $\prod _{n=1}^\infty (1+f_n(z))$ converges. Show that there is a $L\in \R $ such that

\begin{equation*}\Bigl |\prod _{n=1}^N (1+f_n(z))\Bigr |<L\end{equation*}

(Problem 5000) Let $f_n$ and $K$ be as in Problem 4990. Show that the sequence $\bigl \{\prod _{n=1}^N (1+f_n(z))\bigr \}_{N=1}^\infty $ is uniformly Cauchy, and thus converges uniformly.

(Problem 5010) Let $f_n$ and $\Omega $ be as in Theorem 8.1.9. What do Corollary 8.1.8 and Definition 8.1.1 tell you about $f_n(z)$?

(Problem 5020) Let $\Omega \subseteq \C $ be open and connected and let $S\subset \Omega $ be a set with no accumulation points in $\Omega $. Show that $S$ is a countable set. Conclude that if $f:\Omega \to \C $ is holomorphic and not identically zero, then $f$ has at most countably many zeroes.

(Problem 5030) Let $f_n$ and $\Omega $ be as in Theorem 8.1.9. Let $F(z)=\prod _{n=1}^\infty (1+f_n(z))$. Suppose that $f_n\not \equiv 0$ for any $n\in \N $. Show that $F$ has at most countably many zeroes, and so cannot be identically zero.

(Memory 5040) Let $\Omega $, $f_n$ and $F$ be as in Theorem 8.1.9. Then $F(z_0)=0$ if and only if $1+f_n(z_0)=0$ for some $n\geq 1$. Furthermore $1+f_n(z_0)=0$ for at most finitely many values of $n$.

(Problem 5050) Let $\Omega $, $f_n$ and $F$ be as in Theorem 8.1.9. Suppose that $F$ is not identically equal to zero. Let $z_0\in \Omega $ and suppose that $F(z_0)=0$. Show that the multiplicity of the zero of $F$ at $z_0$ is equal to the sum of the multiplicities of the zeros of $1+f_n$ at $z_0$.

8.2. The Weierstraß Factorization Theorem

(Problem 5060) Let $\Omega \subseteq \C $ be open, let $S\subset \Omega $ be a set with no accumulation points in $\Omega $, and let $m:S\to \N $ be a function.

Show that there is a list $\{a_n\}_{n=1}^N$ or sequence $\{a_n\}_{n=1}^\infty $ such that $S=\{a_n:n\in \N \}$ and such that $m(n)=\#\{k:a_k=a_n\}$. Show furthermore that no subsequence of $\{a_n\}_{n=1}^\infty $ converges to a point in $\Omega $.

In particular, if $f:\Omega \to \C $ is holomorphic and not identically zero on any connected component of $\Omega $, show that there is a list $\{a_n\}_{n=1}^N$ or sequence $\{a_n\}_{n=1}^\infty $ such that $\{z\in \Omega :f(z)=0\}=\{a_n:n\in \N \}$ and such that the multiplicity $\mult _f(a_n)$ of the zero of $f$ at $a_n$ is equal to $\#\{k:a_k=a_n\}$, and furthermore no subsequence of $\{a_n\}_{n=1}^\infty $ converges to a point in $\Omega $.

Corollary 8.2.3. Let $\{a_n\}_{n=1}^\infty $ be a sequence of points in $\C $ such that no subsequence converges to a point in $\C $. Then there exists a holomorphic function $f:\C \to \C $ such that $\{z\in \C :f(z)=0\}=\{a_n:n\in \N \}$ and such that the multiplicity $m(a_n)$ of the zero of $f$ at $a_n$ is equal to $\#\{k:a_k=a_n\}$.

(Problem 5061) Show that this is equivalent to the following. Let $S\subset \C $ be a set with no accumulation points and let $m:S\to \N $ be a function. Then there exists a holomorphic function $f:\C \to \C $ such that $\{z\in \C :f(z)=0\}=S$ and such that the multiplicity $\mult _f(z)$ of the zero of $f$ at $z$ is equal to $m(z)$ for all $z\in S$.

(Problem 5070) Compute the power series (centered at zero) for the function $f(z)=\log \frac {1}{1-z}$. Simplify your answer as much as possible.

\begin{equation*}E_p(z)=(1-z) \exp \biggl (z+\frac {z^2}{2}+\dots +\frac {z^p}{p}\biggr ).\end{equation*}

where $a_n\neq 0$ for all $n>N_0$, and where $\{p_n\}_{n=1}^\infty $ is an appropriate sequence of natural numbers.

(Problem 5080) We now begin the proof of Theorem 8.2.2 (and thus of Corollary 8.2.3). Show that $E_p$ is an entire function, that $E_p(z)=0$ if and only if $z=1$, that the multiplicity of the zero of $E_p(z)$ at $1$ is $1$, and that $E_p\to 1$ in $\D $.

(Problem 5090) Show that $E_p'(z)=-z^p\exp (\sum _{k=1}^p \frac {z^k}{k})$ for all $z\in \C $.

(Problem 5100) Let $b_n$ be the coefficients of the power series for $E_p$ centered at zero, so

\begin{equation*}E_p(z)=\sum _{n=0}^\infty b_n\,z^n\end{equation*}

for all $z\in \C $. Observe that $b_0=1$. Show that $b_n=0$ if $1\leq n\leq p$. Hint: What is the order of the zero of $E_p'$ at $0$?

Recall [Problem 1820]: Suppose that $\sum _{n=0}^\infty a_n z^n$ and $\sum _{n=0}^\infty b_n z^n$ are two power series with radius of convergence at least $r$. Show that

\begin{equation*}\sum _{n=0}^\infty \Bigl (\sum _{k=0}^n a_k\, b_{n-k}\Bigr )z^n\end{equation*}

\begin{equation*}\sum _{n=0}^\infty \Bigl (\sum _{k=0}^n a_k\, b_{n-k}\Bigr )z^n = \biggl (\sum _{n=0}^\infty a_n z^n\biggr )\biggl (\sum _{n=0}^\infty b_n z^n\biggr )\end{equation*}

(Problem 5110) Show that $b_n\leq 0$ and is real for all $n\geq p+1$. Hint: Write $E_p'$ as a product of functions whose power series you know.

(Problem 5120) Show that $\sum _{n=p+1}^\infty \abs {b_n}=1$. Hint: Start by computing $E_p(1)$.

(Problem 5130) Show that if $\abs {z}\leq 1$ then $\abs {E_p(z)-1}\leq \abs {z}^{p+1}$.

(Problem 5140) Let $\{a_n\}_{n=1}^\infty \subset \C $ be a sequence of nonzero complex numbers. Suppose that the $a_n$s have no accumulation point in the sense that no subsequence converges. (We do not require that the $a_n$s be distinct.) Show that $\lim _{n\to \infty } \abs {a_n}=\infty $.

(Problem 5150) Let $\{a_n\}_{n=1}^\infty \subset \C $ be a sequence of nonzero complex numbers. Suppose that the $a_n$s have no accumulation point.

Fix an $r>0$. Show that $\sum _{n=1}^\infty \abs {E_n(z/a_n)-1}$ converges uniformly on $\overline D(0,r)$.

Theorem 8.2.4. [The Weierstraß factorization theorem.] Let $f:\C \to \C $ be an entire function that is not identically equal to zero.

If $f$ has finitely many zeros, then there is an entire function $g(z)$, an integer $N_0\geq 0$, and complex numbers $a_n\in \C $ such that

\begin{equation*}f(z)=e^{g(z)}\,\prod _{n=1}^{N_0}(z-a_n).\end{equation*}

Otherwise, there is an entire function $g(z)$, an integer $m\geq 0$, and complex numbers $a_n\in \C $ such that

\begin{equation*}f(z)=e^{g(z)}\,z^m\prod _{n=1}^\infty E_n\biggl (\frac {z}{a_n}\biggr )\end{equation*}

8.3. Weierstraß’s theorem in arbitrary domains

Theorem 8.3.1. (Weierstraß) Let $\Omega \subseteq \C $ be open and let $\{a_n\}_{n=1}^\infty $ be a sequence of points in $\Omega $ such that no subsequence converges to a point in $\Omega $. Then there exists a holomorphic function $f:\Omega \to \C $ such that $\{z\in \Omega :f(z)=0\}=\{a_n:n\in \N \}$ and such that the multiplicity $\mult _f(a_n)$ of the zero of $f$ at $a_n$ is equal to $\#\{k:a_k=a_n\}$.

(Problem 5180) (This is the first step in the proof of Theorem 8.3.1.) Let $\Omega \subsetneq \C $ be an open set and let $\{a_n\}_{n=1}^\infty \subset \Omega $ be a sequence with no accumulation points in $\Omega $. Show that for each $n\in \N $ there is a point $\widehat a_n\in \C \setminus \Omega $ such that $|a_n-\widehat a_n|=\dist (a_n,\partial \Omega )$.

(Problem 5190) We will begin with the case where the sequence $\{a_n\}_{n=1}^\infty $ is bounded. Under the conditions of the previous problem, if in addition we have that there is an $R>0$ such that $a_n\in \overline D(0,R)$ for all $n\in \N $, show that $\lim _{n\to \infty } |a_n-\widehat a_n|=\lim _{n\to \infty }\dist (a_n,\partial \Omega )=0$.

(Problem 5200) Let $\Omega $, $\{a_n\}_{n=1}^\infty $ and $\{\widehat a_n\}_{n=1}^\infty $ be as in Problem 5190. Observe that $E_n\Bigl (\frac {a_n-\widehat a_n}{z-\widehat a_n}\Bigr )$ is holomorphic on $\Omega $. Show that

\begin{equation*}\sum _{n=1}^\infty \Bigl |1-E_n\Bigl (\frac {a_n-\widehat a_n}{z-\widehat a_n}\Bigr )\Bigr |\end{equation*}

converges uniformly on $K_\delta =\{z\in \Omega :\dist (z,\{\widehat a_n:n\in \N \})\geq \delta \}$.

(Problem 5201) Let $F(z)=\prod _{n=1}^\infty E_n\bigl (\frac {a_n-\widehat a_n}{z-\widehat a_n}\bigr )$. Show that $F$ satisfies the conditions of Theorem 8.3.1.

(Problem 5202) Show that there is an $M>0$ such that $\sup _{|z|>M} |F(z)|<\infty $ and $\inf _{|z|>M}|F(z)|>0$.

(Problem 5210) Prove Theorem 8.3.1 in the case where $\{a_n\}_{n=1}^\infty $ is unbounded.

Corollary 8.3.4. Let $\Omega \subseteq \C $ be open. Let $m:\Omega \to \C $ be meromorphic on $\Omega $. Then there exist two holomorphic functions $f$, $g:\Omega \to \C $ such that $m=\frac {f}{g}$.

8.3. The Mittag-Leffler theorem

(Lemma 5221) Let $\{\beta _n\}_{n=1}^\infty \subset \C $ and $\{\gamma _n\}_{n=1}^\infty \subset \C $ be two sequences of complex numbers and let $\{a_n\}_{n=1}^\infty $ be a sequence of distinct complex numbers such that no subsequence has an accumulation point in $\C $. Then there exists an entire function $f$ such that $f(a_n)=\beta _n$ and $f'(a_n)=\gamma _n$ for all $n\geq 1$.

Recall [Problem 5140]: We have that $\lim _{n\to \infty } \abs {a_n}=\infty $.

(Problem 5230) In this problem we begin the proof of Lemma 5221. For each $n\in \N $, show that there is an entire function $g_n$ such that

$g_n(a_n)=\beta _n$, and such that $|g_n(z)|<\frac {1}{2^n}$ for all $z$ with $|z|<\frac {1}{2}|a_n|$.

(Problem 5240) Show that $g=\sum _{n=1}^\infty g_n$ converges normally on $\C $.

(Problem 5250) For each $n\in \N $, show that there is an entire function $h_n$ such that

$h_n'(a_k)=0$ if $k\neq n$, $h_n'(a_n)=\gamma _n-g'(a_n)$, and such that $|h_n(z)|<\frac {1}{2^n}$ for all $z$ with $|z|<\frac {1}{2}|a_n|$. Then show that $f(z)=g(z)+\sum _{n=1}^\infty h_n(z)$ converges normally on $\C $ and satisfies the conditions of Lemma 5221.

Theorem 8.3.6. (Mittag-Leffler) Let $\Omega \subseteq \C $ be open. Let $\{\alpha _n\}_{n=1}^\infty \subset \Omega $ be a sequence of distinct elements with no accumulation points in $\Omega $. For each $n$, let $p_n\in \N $ and suppose that $a_{\ell ,n}\in \C $ is defined for each $n\in \N $ and each $\ell \in \N $ with $-p_n\leq \ell \leq -1$.

Then there is a function $f$ that is meromorphic in $\Omega $, whose singular set is $\{\alpha _n:n\in \N \}$, and such that

\begin{equation*}f(z)-\sum _{\ell =-p_n}^{-1} a_{\ell ,n}(z-\alpha _n)^{\ell }\end{equation*}

Lemma 8.3.5. [Pole-pushing lemma]. Let $\alpha $, $\beta \in \C $. Suppose that

\begin{equation*}A(z)=\sum _{j=-M}^{-1} a_j(z-\alpha )^j\end{equation*}

for some $M\in \N $ and some $a_j\in \C $. Then for all $r>|\alpha -\beta |$ and all $\varepsilon >0$ we have that there is a $N\in \N $ and numbers $b_j\in \C $ such that

\begin{equation*}\Bigl |A(z)-\sum _{j=-N}^{-1} b_j (z-\beta )^j\Bigr |<\varepsilon \end{equation*}

(Problem 5270) Prove Theorem 8.3.6 in the case where $\{\alpha _n\}_{n=1}^\infty $ is bounded.

[Chapter 8, Problem 23] Theorem 8.3.6 is still true even if $\{\alpha _n\}_{n=1}^\infty $ is unbounded.

Theorem 8.3.8. Let $\Omega \subseteq \C $ be open. Let $\{\alpha _n\}_{n=1}^\infty \subset \Omega $ be a sequence of distinct elements with no accumulation points in $\Omega $. For each $n$, let $p_n$, $q_n\in \N $ and suppose that $a_{\ell ,n}\in \C $ is defined for each $n\in \N $ and each $\ell \in \N $ with $-p_n\leq \ell \leq q_n$.

Then there is a function $f$ that is meromorphic in $\Omega $, whose singular set is (a subset of) $\{\alpha _n:n\in \N \}$, and such that

\begin{equation*}f(z)-\sum _{\ell =-p_n}^{q_n} a_{\ell ,n}(z-\alpha _n)^{\ell }\end{equation*}

has a removable singularity at $\alpha _n$ and whose Laurent series expansion about $\alpha _n$ may be written as

\begin{equation*}f(z)=\sum _{\ell =-p_n}^{\infty } c_{\ell ,n} (z-\alpha _n)^{\ell }\end{equation*}

We may equivalently say that, for each $\alpha _n$, there is an $r_n>0$ such that $D(\alpha _n,r_n)\subseteq \Omega $ contains no other $\alpha _k$s and such that

\[f(z)=\sum _{\ell =-p_n}^{q_n} a_{\ell ,n} (z-\alpha _n)^{\ell }+\sum _{\ell =q_n+1}^{\infty } c_{\ell ,n} (z-\alpha _n)^{\ell }\]

Lemma 8.3.7. Suppose that the numbers $p$, $q$, and $a_\ell $ for $-p\leq \ell \leq q$ are given. Let $\Omega \subseteq \C $ be open, let $\alpha \in \Omega $, and let $g:\Omega \to \C $ be holomorphic. Suppose further that $p$, $q\geq 0$ and that $g$ has a zero of multiplicity $q+1$ at $\alpha $. Then there exist numbers $b_\ell $, $c_\ell \in \C $ such that

\begin{equation*}g(z)\sum _{\ell =-1-p-q}^{-1} b_\ell (z-\alpha )^\ell =\sum _{\ell =-p}^q a_\ell (z-\alpha )^\ell +\sum _{\ell =q+1}^\infty c_\ell (z-\alpha )^\ell \end{equation*}

(Problem 5280) (This is the first step in the proof of Lemma 8.3.7.) Suppose that $\sum _{\ell =q+1}^\infty d_\ell (z-\alpha )^\ell $ and $\sum _{\ell =-p-q-1}^\infty b_\ell (z-\alpha )^\ell $ are two Laurent series that converge in $D(\alpha ,r)\setminus \{\alpha \}$. Show that

\begin{equation*} \sum _{n=-p}^\infty \Bigl (\sum _{k=q+1}^{n+p+q+1} b_{n-k} d_{k}\Bigr )(z-\alpha )^{n} \end{equation*}

\begin{equation*} \sum _{n=-p}^\infty \Bigl (\sum _{k=q+1}^{n+p+q+1} b_{n-k} d_{k}\Bigr )(z-\alpha )^{n} = \Bigl (\sum _{\ell =q+1}^\infty d_\ell (z-\alpha )^\ell \Bigr ) \Bigl (\sum _{\ell =-p-q-1}^\infty b_\ell (z-\alpha )^\ell \Bigr ) \end{equation*}

8.3. Maximal domains of existence of holomorphic functions

Corollary 8.3.3. (Special case) There is a function $f:\D \to \C $ that is holomorphic in $\D $ such that, if $\D \subseteq {W}$, $W$ is open and connected, $F:{W}\to \C $ is holomorphic, and $F=f$ in $\D $, then ${W}=\D $. (That is, there is a function $f$ holomorphic in $\D $ that cannot be extended to a function holomorphic in any larger open set.)

(Problem 5310) Let $g(e^{i\theta })=\sum _{n=0}^\infty \frac {5^n}{6^n}\cos (7^n \theta )$. (This is a special case of the Weierstraß function.) Show that $g$ is well-defined (the sum converges) for all $0\leq \theta \leq 2\pi $ and that $g$ is continuous on $\partial \D $.

(Problem 5320) Let $u$ be the function that is harmonic in $\D $, continuous on $\overline \D $ and with $u(e^{i\theta })=g(e^{i\theta })$ for $0\leq \theta \leq 2\pi $. Let $f$ be the function that is holomorphic in $\D $ with real part $u$. ($u$ and $f$ exist by Theorem 7.3.4 and Lemma 7.1.4.)

Show that $f$ satisfies the conditions of Corollary 8.3.3. Hint: Use the fact (proven by Weierstraß in 1872) that $g(\theta )$ is nowhere differentiable.

Corollary 8.3.3. Let $\Omega \subsetneq \C $ be any nonempty open set that is not all of $\C $. Then there is a function $f:\Omega \to \C $ that is holomorphic in $\Omega $ such that, if $\Omega \subseteq W$, $W$ is open and connected, $F:W\to \C $ is holomorphic, and $F=f$ in $\Omega $, then $\Omega =W$. (That is, there is a function $f$ holomorphic in $\Omega $ that cannot be extended to a function holomorphic in any larger open set.)

be the grid of squares in $\C $ with side-length $2^j$ aligned with the axes. Show that if $z\in \C $ and $j\in \Z $ then $x\in S$ for exactly one $S\in \mathcal {Q}_j$. Here is a sketch of (the cubes in) $\mathcal {Q}_j$.

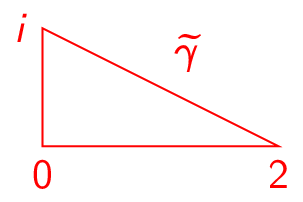
(Problem 5322) Suppose that $S\in \mathcal {Q}_j$. Let $P(S)$ be the “dyadic parent” of $S$, so $S\subsetneq P(S)\in \mathcal {Q}_{j+1}$. Let $2S$ be the square concentric to $S$ of side-length $2^{j+1}$.

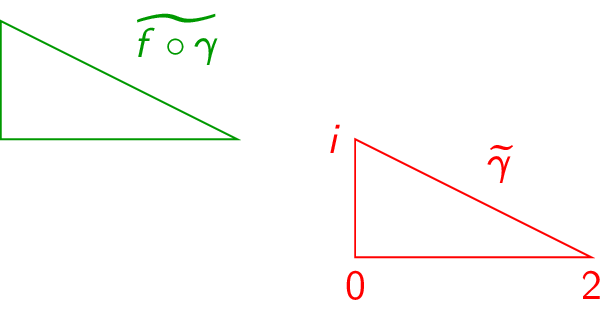
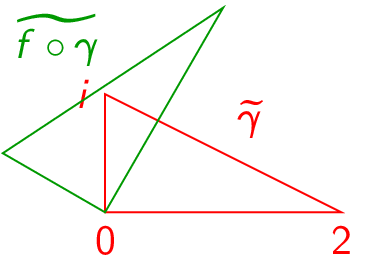
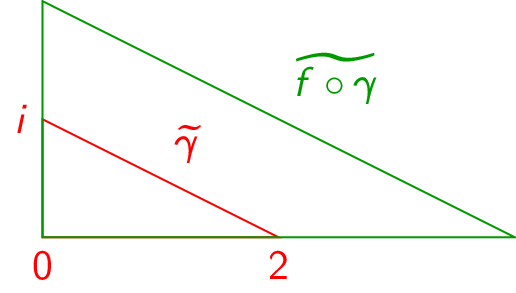
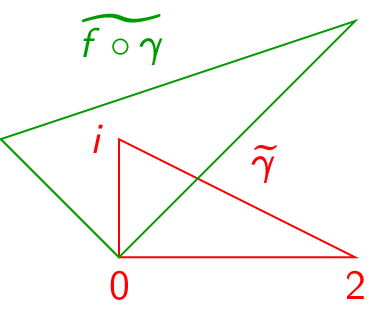
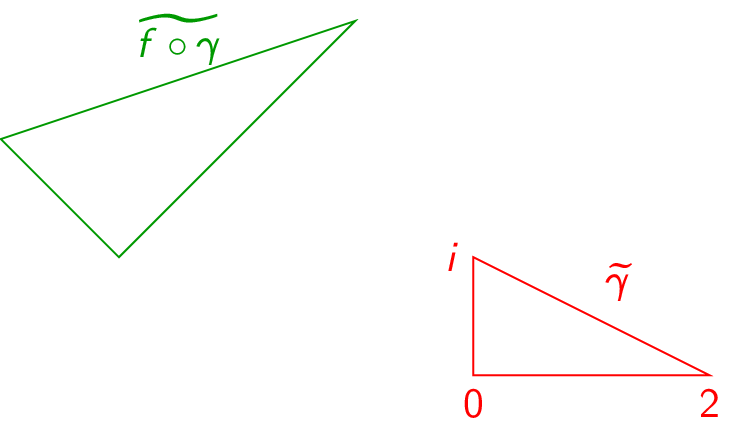
(Problem 5330) If $S\in \mathcal {Q}_j$, let $\ell (S)=2^j$ be the side-length of $S$. Show that if $S\in \mathcal {Q}_j$ and $z\in S$, then $D(z,\ell (S)/2)\subset 2S$ and $2P(S)\subset \overline D(z,3\sqrt {2}\ell (S))$.

(Problem 5340) Let $\mathcal {Q}=\cup _{j=-\infty }^\infty \mathcal {Q}_j$. Let $\Omega \subsetneq \C $ be open. Let $\mathcal {G}=\{S\in \mathcal {Q}:2S\subset \Omega ,\>2P(S)\not \subset \Omega \}$. We call $\mathcal {G}$ a dyadic Whitney decomposition of $\Omega $. Show that $\cup _{S\in {\mathcal {G}}} S=\Omega $.

Here is a sketch of (the cubes in) $\mathcal {G}$ in the case where $\Omega $ is a disc:

(Problem 5341) If $k<j$ and $j$, $k\in \Z $, and if $S\in \mathcal {Q}_k$, show that there is exactly one $T\in \mathcal {Q}_j$ with $S\subset T$ and that $S\cap R=\emptyset $ for every other $R\in \mathcal {Q}_j$.

(Problem 5350) Show that if $S\in {\mathcal {G}}$ and $T\in \mathcal {G}$, then either $S=T$ or $S\cap T=\emptyset $. If $z\in \Omega $, then how many cubes $S\in \mathcal {G}$ can satisfy $z\in S$?

(Problem 5370) Suppose that $S$, $T\in \mathcal {G}$ and that $\dist (S,T)=0$; that is, the closures of $S$ and $T$ intersect. Show that $\ell (S)\leq 4\ell (T)$ and that $\ell (T)\leq 4\ell (S)$.

(Problem 5380) If $S\in \mathcal {G}$, let $z_S$ be the midpoint of $S$. Let $A=\{z_S:S\in \mathcal {G}\}$.

Let $z\in \Omega $. Show that $z$ is not an accumulation point for $A$. Hint: if $z\in T\in \mathcal {G}$, then how many midpoints $z_S$ can appear in $D(z,\ell (T)/8)$?

(Problem 5390) Let $z\in \partial \Omega $. Show that $z$ is an accumulation point for $A$.

(Problem 5400) Prove Corollary 8.3.3. Hint: Let $f$ be the function holomorphic in $\Omega $ and such that $f(z)=0$ (with multiplicity one) if and only if $z\in A$ given by Theorem 8.3.1. Show that the domain of existence of $f$ is $\Omega $; that is, if $\widetilde f=f$ in $\Omega $ and $\widetilde f$ is holomorphic on some open set $\Psi \supseteq \Omega $, then $\Psi =\Omega $.

9.1. Jensen’s Formula and an Introduction to Blaschke Products

Recall [Theorem 8.3.1]: If $\{a_n\}_{n=1}^\infty \subset \D $ and no subsequence converges to a point in $\D $, then there is a holomorphic function $f:\D \to \C $ such that $\{z\in \Omega :f(z)=0\}=\{a_n:n\in \N \}$ and such that the multiplicity $\mult _f(a_n)$ of the zero of $f$ at $a_n$ is equal to $\#\{k:a_k=a_n\}$.

Theorem 9.1.4. Suppose that $f:\D \to \C $ is a bounded nonconstant holomorphic function. Let $\{a_k\}_{k=1}^\infty $ be the zeroes of $f$ (with multiplicity). Then

(Problem 5410) Give an example of a sequence $\{a_k\}_{k=1}^\infty \subset \D $ such that no subsequence converges to a point in $\D $ and such that $\sum _{k=1}^\infty (1-|a_k|)=\infty $. Give an example of a function holomorphic in $\D $ that satisfies $\{z\in \D :f(z)=0\}=\{a_k:k\in \N \}$.

then $\phi _a$ is a holomorphic bijection from $\D $ to itself, a continuous bijection from $\partial \D $ to itself, and a continuous bijection from $\overline \D $ to itself.

Proposition 9.1.1. $\phi _a$ is holomorphic on an open neighborhood of $\overline \D $. $\phi _a(z)=0$ if and only if $z=a$ and the zero at $a$ is simple. Finally, $|\phi _a(z)|=1$ if $|z|=1$.

Theorem 9.1.2. (Jensen’s formula.) Let $f$ be holomorphic in a neighborhood of $\overline D(0,r)$ and suppose $f(0)\neq 0$. Let $a_1,a_2,\dots ,a_n$ be the zeros of $f$ in $D(0,r)$ counted with multiplicity. Assume that $f$ has no zeroes on $\partial D(0,r)$.

\[\log |f(0)|+\sum _{k=1}^n \log \biggl |\frac {r}{a_k}\biggr |=\frac {1}{2\pi } \int _0^{2\pi } \log |f(re^{i\theta })|\,d\theta .\]

(Problem 5420) Show that Theorem 9.1.2 is valid in the following two special cases:

(Problem 5430) Justify the (implicit) claim in Theorem 9.1.2 that $f$ has at most finitely many zeroes in $\overline D(0,r)$. Then prove Theorem 9.1.2.

(Problem 5440) Suppose that $f$ has a zero of multiplicity $m\geq 1$ at $0$. What does Jensen’s formula tell you about $\log |\lim _{z\to 0} \frac {f(z)}{z^m}|$?

Theorem 9.1.5. Suppose that $m\in \N _0$, $\{a_k\}_{k=1}^\infty \subset \D \setminus \{0\}$, and that $\sum _{k=1}^\infty (1-|a_k|)<\infty $. Then there is a bounded holomorphic function $f:\D \to \D $ such that $f$ has a zero of multiplicity $m$ at zero (or $f(0)\neq 0$ if $m=0$), $\{z\in \D \setminus \{0\}:f(z)=0\}=\{a_n:n\in \N \}$, and such that the multiplicity $\mult _f(a_n)$ of the zero of $f$ at $a_n$ is equal to $\#\{k:a_k=a_n\}$. Furthermore, one such $f$ is given by Problem 5470 below.

(Problem 5452) Show that $\phi _a(0)=-a$ for all $a\in \D $ and thus, if $w\in \partial \D $, then $\lim _{\substack {a\to w\\a\in \D }} \phi _a(0)=-w$.

for any $z\in \D $, and that the convergence is uniform for $z$ in any compact subset of $\D $.

where $m\geq 0$ is an integer (written $m\in \N _0$) and where $a_k\in \D \setminus \{0\}$ for all $k$. (If $\sum _{k=1}^\infty (1-|a_k|)<\infty $, then the Blaschke product converges to a holomorphic function on $\D $.)

Corollary 9.1.6. If $f:\D \to \C $ is a bounded holomorphic function with a zero of multiplicity $m\in \N _0$ at $0$ (including the case $m=0$ where $f(0)\neq 0$), and if $\{a_k\}_{k=1}^N$, $N\in \N _0\cup \{\infty \}$, is the list of the other zeroes of $f$ counted with multiplicity, then there is a holomorphic function $g:\D \to \D $ such that $\re g$ is bounded above (meaning $e^g$ is bounded in modulus) and such that

(Problem 5490) Prove that $\sup _{\D } |f|=\sup _{\D }|e^g|$. This completes the proof of Corollary 9.1.6.

9.2. The Hadamard Gap Theorem

Please see Professor Barton’s video lecture (posted to Blackboard) for material concerning the Hadamard gap theorem.

9.3. Entire Functions of Finite Order

Lemma 9.3.1. Let $f$ be an entire function with $f(0)=1$. If $r>0$ and $b>1$, then

where $n(r)$ denotes the number of zeroes of $f$ (with multiplicity) in $D(0,r)$.

Recall [Theorem 3.4.4]: If $f$ is entire and there is a constant $C\in \R $ and a $k\in \N _0$ such that $|f(z)|\leq C+C|z|^k$ for all $z\in \C $, then $f$ is a polynomial of degree at most $k$, and so by Theorem 3.4.5 $f$ has exactly $k$ zeroes counted with multiplicity.

[Definition: Order of an entire function] If $f:\C \to \C $ is entire and there are positive real constants $a$ and $r$ such that

(Exercise 5502) Let $f$ be a function of finite order and let $p$ be a polynomial. Show that $f+p$ is a function of finite order and that its order is equal to that of $f$.

(Exercise 5503) Let $f$ be a function of finite order and let $p$ be a polynomial. Show that $fp$ is a function of finite order and that its order is equal to that of $f$.

Theorem 9.3.2. Suppose that $f$ is an entire function of finite order $\lambda \geq 0$, with $f(0)=1$ and with infinitely many zeroes. If the zeroes of $f$ (with multiplicity) are $\{a_k\}_{k=1}^\infty $, and if $\varepsilon >0$, then

(Problem 5520) Rewrite and prove Theorem 9.3.2 without the assumption $f(0)=1$.

Theorem 9.3.7. (Simplified.) Suppose that $f$ is an entire function of finite order and that $f$ has finitely many zeroes.

Then $f(z)=p(z)e^{q(z)}$, where $p$ is a polynomial and $q$ is a polynomial whose degree is equal to the order of $f$.

Theorem 9.3.9. If $c\in \C $ and $f$ is an entire function of finite order $\lambda \notin \Z $, then the equation $f(z)=c$ has infinitely many solutions.

Theorem 9.3.10. If $f$ is an entire function of finite order, then $\C \setminus f(\C )$ can contain at most one point.

Lemma 9.3.4. Suppose that $f$ is an entire function of finite order $\lambda $ and that $f(0)=1$. Suppose that $z\in \C $ and that $p\in \Z $ with $p>\lambda -1$. Then

\[\lim _{r\to \infty } \frac {1}{2\pi }\int _0^{2\pi } 2re^{i\theta } (re^{i\theta }-z)^{-p-2} \log |f(re^{i\theta })| \,d\theta = 0.\]

[Chapter 9, Problem 1] If $f$ is holomorphic in a neighborhood of $\overline D(0,r)$ and $z_0\in D(0,r)$, and if $f$ has no zeroes in $\overline D(0,r)$, then

\[\log |f(z_0)| = \frac {1}{2\pi } \int _0^{2\pi } \re \left (\frac {re^{i\theta }+z_0}{re^{i\theta }-z_0}\right ) \log |f(re^{i\theta })|\,d\theta .\]

Proposition 9.3.5. (Simplified.) Suppose that $g$ is a nonconstant entire function and that $h=e^g$ is a function of finite order $\lambda $. If $p>\lambda -1$ is an integer, then

10.1. Definition of an analytic function element

(Problem 5571) Let $\Psi \subsetneq \Omega \subseteq \C $, where $\Psi $ is open and nonempty and $\Omega $ is open and connected. Suppose that $f$ is holomorphic in $\Psi $. Show that there is at most one function $F$ that is holomorphic in $\Omega $ and such that $F=f$ in $\Psi $.

(Problem 5580) Suppose that $\Omega $, $W$ are connected open sets with $D(1,1)\subsetneq \Omega \subset \C $ and $D(1,1)\subsetneq W\subset \C $. Suppose that $F:\Omega \to \C $ and $G: W\to \C $ are holomorphic and that $G(z)=F(z)=\ln z = \ln z=\sum _{k=0}^\infty \frac {(-1)^k}{k}(z-1)^k$ for all $z\in D(1,1)$.

If $U$ is a connected component of $\Omega \cap W$, show that there is a $n\in \Z $ such that $F(z)=G(z)+2\pi i n$ for all $z\in U$. Give an example to show that $n$ may not equal zero.

(Problem 5590) Suppose that $\Omega $, $W$ are connected open sets with $D(1,1)\subsetneq \Omega \subset \C $ and $D(1,1)\subsetneq W\subset \C $. Suppose that $F:\Omega \to \C $ and $G: W\to \C $ are holomorphic and that $G(z)=F(z)=\sqrt {z}$ for all $z\in D(1,1)$. (Here $\sqrt {z}$ is the unique function continuous on $D(1,1)$ such that $\sqrt {z}^2=z$ and $\sqrt {1}=1$.)

If $U$ is a connected component of $\Omega \cap W$, show that either $F(z)=G(z)$ for all $z\in U$ or $F(z)=-G(z)$ for all $z\in U$. Give an example to show that the case $F(z)=-G(z)$ can occur.

Definition 10.1.4. A function element is an ordered pair $(f,D(P,r))$ where $P\in \C $, $r>0$ and $f$ is a holomorphic function defined on $D(P,r)$.

Definition 10.1.5. If $(f,D(P,r))$ and $(g,D(Q,s))$ are function elements, if $D(P,r)\cap D(Q,s)\neq \emptyset $, and if $f=g$ on $D(P,r)\cap D(Q,s)$, we say that $(g,D(Q,s))$ is a direct analytic continuation of $(f,D(P,r))$.

[Definition: Analytic continuation] Suppose that we have a finite sequence of function elements $\{(f_j,D(P_j,r_j))\}_{j=1}^k$ such that $(f_j,D(P_j,r_j))$ is a direct analytic continuation of $(f_{j-1},D(P_{j-1},r_{j-1}))$ for all $1<j\leq k$. Then $(f_k,D(P_k,r_k))$ is an analytic continuation of $(f_1,D(P_1,r_1))$.

(Problem 5600) Find a function element $(f,D(P,r))$ and two distinct function elements $(g,D(Q,s))$ and $(\tilde g,D(Q,s))$, with the same disc $D(Q,s)$, such that $(g,D(Q,s))$ and $(\tilde g,D(Q,s))$ are both analytic continuations of $(f,D(P,r))$. Can you do this for a direct analytic continuation?

10.2. Analytic continuation along a curve

Definition 10.2.1. Let $\gamma :[0,1]\to \C $ be a continuous function (we will call $\gamma $ a curve). Let $r>0$, let $D=D(\gamma (0),r)$ and let $(f, D)$ be a function element. An analytic continuation of $(f, D)$ along $\gamma $ is a collection of function elements $\{(f_t,D_t)\}_{0\leq t\leq 1}$ such that:

Proposition 10.2.2. Let $\gamma :[0,1]\to \C $ be a curve and let $(f,D)$ be a funcion element with $D=D(\gamma (0),r)$ for some $r>0$. Let $\{(g_t,D_t)\}_{0\leq t\leq 1}$ and $\{(h_t,B_t)\}_{0\leq t\leq 1}$ be two analytic continuations of $(f,D)$ along $\gamma $.

(Problem 5601) Let $S=\{t\in [0,1]:g_t=h_t$ in $D_t\cap B_t\}$. Begin the proof of Proposition 10.2.2 by showing that $S$ is relatively open in $[0,1]$.

(Problem 5610) Complete the proof of Proposition 10.2.2 by showing that $S$ is closed.

(Problem 5620) Suppose that $\gamma :[0,1]\to \C $ is a closed curve (so $\gamma (1)=\gamma (0)$). Let $\{(f_t,D(\gamma (t),r_t))\}_{0\leq t\leq 1}$ be an analytic continuation of $(f, D(\gamma (0),r))$ along $\gamma $. Is it necessarily true that $f_1=f_0$ on $D(\gamma (0),\min (r_0,r_1))$?

(Exercise 5621) Let $\gamma (t)=e^{it}$, $0\leq t\leq 6\pi $. Let $(f,D(P,r))=(\log z, D(1,1/2))$ be a function element. Let $\{(f_t,D(\gamma (t),r_t))\}_{0\leq t\leq 6\pi }$ be an analytic continuation of $(\log z, D(1,1/2))$ along $\gamma $.

(Exercise 5622) Let $\gamma (t)=e^{it}$, $0\leq t\leq 6\pi $. Let $(g,D(P,r))=(\sqrt {z}, D(1,1/2))$ be a function element. Let $\{(g_t,D(\gamma (t),r_t))\}_{0\leq t\leq 6\pi }$ be an analytic continuation of $(\sqrt {z}, D(1,1/2))$ along $\gamma $.

10.3. The Monodromy Theorem

Definition 10.3.1. Let $a<b$, $c<d$. Let $\Omega \subseteq \C $ be open and connected. Let $\gamma _c$, $\gamma _d:[a,b]\to \Omega $ be two continuous4 curves with the same endpoints (so $\gamma _c(a)=\gamma _d(a)$, $\gamma _c(b)=\gamma _d(b)$).

We say that $\gamma _c$ and $\gamma _d$ are homotopic in $\Omega $ if there is a function $\Gamma $ such that:

Definition 10.3.2. Let $\Omega \subseteq \C $ be open and connected, $D=D(P,r)\subseteq \Omega $, and let $(f,D)$ be a function element. We say that $(f,D)$ admits unrestricted continuation in $\Omega $ if, for every continuous curve $\gamma :[0,1]\to \Omega $ with $\gamma (0)=P$, there is an analytic continuation of $(f,D)$ along $\gamma $.

(Exercise 5623) Prove directly (without Theorem 10.3.3 or Corollary 10.3.4) that $(\ln ,D(1,1/2))$ does not admit unrestricted continuation in $\C $.

Theorem 10.3.3. [The monodromy theorem]. Let $\Omega \subseteq \C $ be open and connected, $D=D(P,r)\subseteq \Omega $, and let $(f,D)$ be a function element. Assume that $(f,D)$ admits unrestricted continuation in $\Omega $.

Let $\gamma _0$, $\gamma _1:[0,1]\to \Omega $ be homotopic curves in $\Omega $ with $\gamma _0(0)=\gamma _1(0)=P$. If $s\in [0,1]$, let $\{(f_{t,s},D_{t,s})\}_{0\leq t\leq 1}$ be an analytic continuation of $(f,D(P,r))$ along $\gamma _s$.

Then $f_{1,s}=f_{1,\sigma }$ in $D_{1,s}\cap D_{1,\sigma }$. for all $s$, $\sigma \in [0,1]$. In particular, $f_{1,0}=f_{1,1}$ in $D_{1,0}\cap D_{1,1}$.

(Problem 5630) Suppose that $(f,D)$ is a function element, $D=D(P,r)$, $\gamma :[0,1]\to \C $ is a curve with $\gamma (0)=P$, and that there exists an analytic continuation $\{(f_t,D(\gamma (t),r_t))\}_{t\in [0,1]}$ of $(f,D)$ along $\gamma $.

Show that there is also an analytic continuation along $\gamma $ such that the radius $r_t$ is a constant. Can you do this in such a way that the $\varepsilon =\varepsilon _t$ in Definition 10.2.1 is also a constant?

(Proposition 5631) Let $\gamma :[0,1]\to \C $ be a curve. Let $D=D(\gamma (0),r)$, let $(f,D)$ be a function element, and let $\{(g_t,D(\gamma (t),r))\}_{t\in [0,1]}$ be an analytic continuation of $(f,D)$ along $\gamma $ such that the discs in the definition of analytic continuation all have the same radii.

Let $\eta :[0,1]\to \C $ be a curve. Suppose that $|\eta (t)-\gamma (t)|<r$ for all $t\in [0,1]$. Suppose that $\eta (0)=\gamma (0)$ and that $\{(h_t,D(\eta (t),\varrho ))\}_{t\in [0,1]}$ is an analytic continuation of $(f,D)$ along $\eta $ (possibly with a different radius for the discs in the definition of analytic continuation).

Then $(h_t,D(\eta (t),\varrho ))$ is a direct analytic continuation of $(g_t,D(\gamma (t),r))$ for all $t$. In particular, if $\gamma (t)=\eta (t)$ then $g_t=h_t$ in $D(\eta (t),\min (r,\varrho ))$.

(Problem 5640) Begin the proof of Proposition 5631 as follows. Let $S=\{t\in [0,1]:g_t=h_t$ in $D(\gamma (t),r)\cap D(\eta (t),\varrho )\}$. Show that $S$ is relatively open in $[0,1]$.

(Problem 5650) Complete the proof of Proposition 5631 by showing that $S$ is closed.

Corollary 10.3.4. Let $\Omega \subseteq \C $ be open and simply connected and let $(f,D(P,r))$ be a function element with $D(P,r)\subseteq \Omega $. Assume that $(f,D(P,r))$ admits unrestricted continuation in $\Omega $. Then there exists a unique function $F:\Omega \to \C $ that is holomorphic in $\Omega $ and satisfies $F=f$ in $D(P,r)$.

10.4. Topology

[Definition: Covering space] Let $W$, $\Omega $ be two topological spaces. Suppose that there is a continuous function $\pi :W\to \Omega $ such that, if $z\in \Omega $, then there is a connected open set $U$ with $x\in U\subset \Omega $ and such that, if $V$ is a connected component of $\pi ^{-1}(U)$, then $\pi :V\to U$ is a homeomorphism. Then we say that $W$ is a covering space for $\Omega $.

(Problem 5661) $\R $ is a covering space for $S^1=\{(x,y)\in \R ^2:|(x,y)|=1\}$ under the mapping $\pi (t)=(\cos t,\sin t)$.

(Bonus Problem 5662) If $\Omega $ is path connected and also simply connected, show that $\pi $ must be a homeomorphism from $W$ to $\Omega $.

(Problem 5663) Let $\gamma :[0,1]\to \C $ be a $C^1$ curve. Show that $\ell (\gamma )\geq |\gamma (1)-\gamma (0)|$ and that, if $\ell (\gamma )=|\gamma (1)-\gamma (0)|$, then $\gamma $ must be a parameterization of the straight line segment from $\gamma (0)$ to $\gamma (1)$.

(Problem 5664) Let $\Omega \subset \C $ be open and connected. If we define ${d}(z,w)=\inf \{\ell (\gamma )\mid \gamma :[0,1]\to \Omega $ is $C^1,\gamma (0)=z,\gamma (1)=w\}$, show that $(\Omega ,{d})$ is a metric space.

(Problem 5670) Let $d$ and $\Omega $ be as in the previous problem. Show that if $D(z,r)\subset \Omega $, then $|z-w|<r$ if and only if ${d}(z,w)<r$, and ${d}(w_1,w_2)=|w_1-w_2|$ for all $w_1$, $w_2\in D(z,r)$.

(Problem 5671) Let $\Omega \subset \C $ be open and connected and let $d$ be as in Problem 5664.

where $\gamma \sim \eta $ if $\gamma (1)=\eta (1)$ and $\gamma $ and $\eta $ are homotopic.

If $\gamma _1\in \widetilde \gamma _1$, $\eta \in \widetilde \eta \in W$, let

\[\delta (\widetilde \gamma _1,\widetilde \eta )=\inf \{\ell (\gamma _2):\gamma _2(0)=\gamma _1(1),\gamma _2(1)=\eta (1),\gamma _1*\gamma _2\text { is homotopic to~}\eta \},\]

where $\gamma _1*\gamma _2=\gamma _3$ is given from $\gamma _1$ and $\gamma _2$ by Problem 1050.

(Problem 5672) Define $\pi :W\to \Omega $ by $\pi (\widetilde \gamma )=\gamma (1)$ for some (hence any $\gamma \in \widetilde \gamma $. Show that if $\widetilde \eta $, $\widetilde \gamma \in W$, then $|\pi (\widetilde \eta )-\pi (\widetilde \gamma )|\leq \delta (\widetilde \eta ,\widetilde \gamma )$.

(Problem 5690) Suppose that $D(z,r)\subset \Omega $. Show that if $\pi (\widetilde \gamma )\in D(z,r)$ and $\pi (\widetilde \eta )\in D(z,r)$, then either $\delta (\widetilde \gamma ,\widetilde \eta )=|\pi (\widetilde \gamma )-\pi (\widetilde \eta )|$ or $\delta (\widetilde \gamma ,\widetilde \eta )\geq 2r-|z-\pi (\widetilde \gamma )|-|z-\pi (\widetilde \eta )|$.

(Problem 5680) Suppose $\gamma \in \widetilde \gamma \in W$ and that $D(\pi (\widetilde \gamma ),r)\subset \Omega $. Show that $\pi $ is an isomorphism of metric spaces from $B(\widetilde \gamma ,r)$ to $D(\pi \widetilde (\gamma ),r)$, that is, that $\pi (B(\widetilde \gamma ,r))=D(\pi (\widetilde \gamma ),r)$ and that $\delta (\widetilde \zeta , \widetilde \eta )=|\pi (\widetilde \zeta )-\pi (\widetilde \eta )|$ for all $\widetilde \zeta $, $\widetilde \eta \in B(\widetilde \gamma ,r)$.

10.4. The Idea of a Riemann Surface

(Problem 5700) Let $\Omega \subset \C $ be open. Let $D\subset \Omega $ and let $(f,D)$ be a function element that admits unrestricted continuation in $\Omega $.

where $\gamma \sim \eta $ if $\eta (1)=\gamma (1)$ and the analytic continuations $\{g_t,D(\gamma (t),r_t)\}_{t\in [0,1]}$ and $\{h_t,D(\eta (t),q_t)\}_{t\in [0,1]}$ of $(f,D)$ along $\gamma $ and $\eta $, respectively, satisfy $g_t=h_t$ in $D(\gamma (1),r_1)\cap D(\eta (1),q_1)$.

Show that if $\gamma $ and $\eta $ are homotopic then $\gamma \sim \eta $. Give an example to show that the reverse may not be true.

(Problem 5711) Show that $W$ is a covering of $\Psi $ and that $\Psi $ is a covering of $\Omega $.

10.5. Picard’s Theorem

(Problem 5720) Let $f:\C \to \C $ be entire and not constant. Show that $f(\C )$ is dense in $\C $.

Theorem 10.5.5. Let $f:\C \to \C $ be entire and not constant. Then $\C \setminus f(\C )$ contains at most one point.

Recall [Problem 3620]: Let $f:\H \to \H $ be a function. Then $f$ is a biholomorphic self-map if and only if $f(z)=\frac {az+b}{cz+d}$ for some real numbers $a$, $b$, $c$, and $d$ that satisfy $ad-bc>0$.

(Problem 5730) Let $G$ be the set of all fractional linear transformations that may be written $f(z)=\frac {az+b}{cz+d}$ where $a$, $b$, $c$, and $d$ are integers that satisfy $ad-bc=1$. Show that if $f$, $g\in G$ then $f\circ g\in G$ and $f^{-1}\in G$. (Thus $G$ is a group under function composition.)

Theorem 10.5.4. There is a function $\lambda :\H \to \C $ (called the modular function) and a nontrivial subgroup $\Gamma $ of $G$ with the following properties.

(Problem 5740) Assume Theorem 10.5.4 is correct. Let $f:\C \to \C $ be entire and suppose that $0$, $1\notin f(\C )$.

Suppose that $z\in \C $ and $w\in \H $ satisfy $f(z)=\lambda (w)$. Show that there is a $\varrho =\varrho _z>0$ and a holomorphic function $k=k_{z,w}:D(z,r)\to \H $ such that $k(z)=w$ and $f(\zeta )=\lambda (k(\zeta ))$ for all $z\in D(z,\varrho )$.

(Problem 5750) Let $z$, $\zeta \in \C $, and let $f(z)=\lambda (w)$, $f(\zeta )=\lambda (\zeta )$. Suppose that $D(z,\varrho _z)\cap D(\zeta ,\varrho _\zeta )\neq \emptyset $. Show that there is a $h\in \Gamma $ such that $h\circ k_{z,w}=k_{\zeta ,\omega }$ in $D(z,\varrho _z)\cap D(\zeta ,\varrho _\zeta )$.

(Problem 5760) Let $D=D(0,\varrho _0)$. Let $w\in \lambda ^{-1}(f(0))$. Show that $(k_{0,w},D)$ admits unrestricted continuation in $\C $, and that every function element $(\tilde k,\widetilde D)$ in the analytic continuation satisfies $\tilde k(\widetilde D)\subseteq \H $.

10.5. The Elliptic Modular Group

Recall [Problem 5730]: The modular group $G$ is the set of all fractional linear transformations that may be written $f(z)=\frac {az+b}{cz+d}$ where $a$, $b$, $c$, and $d$ are integers that satisfy $ad-bc=1$.

Recall [Theorem 10.5.4]: There is a nontrivial subgroup $\Gamma $ of $G$ with the following property.

[Chapter 10, Problem 16] Let $\mu (z)=\frac {z}{2z+1}$, $\omega (z)=z+2$. Let

\[\Gamma =\{h:\H \to \C \mid h(z)=\frac {az+b}{cz+d}, a, b, c, d\in \Z , \>ad-bc=1,\> a, d\text { odd},\>b,c\text { even}\}.\]

Then $\mu $, $\omega \in \Gamma $, $\Gamma $ is a group, and $\mu $ and $\omega $ are a set of generators for $\Gamma $, that is, every $h\in \gamma $ may be written as a composition of finitely many copies of $\mu $, $\omega $, $\mu ^{-1}$, $\omega ^{-1}$, in some order.

(Problem 5780) We now begin the proof of Theorem 10.5.4. If $k\in \Z $, let $L_k=\{k+it:0<t<\infty \}$ be the vertical line segment with one end at $k$.

(Problem 5790) Show that if $h_1$, $h_2\in \Gamma $, then either $h_1(L_0\cup L_1)\cap h_2(L_0\cup L_1)=\emptyset $ or $h_1=h_2$.

(Problem 5800) Show that $\bigcup _{h\in \Gamma } h(L_0\cup L_1)$ is relatively closed in $\H $.

(Problem 5810) Suppose that $U$ is a connected component of $\H \setminus \bigcup _{h\in \Gamma } h(L_0\cup L_1)$. If $g\in \Gamma $, show that $g(U)$ is also a connected component of $\H \setminus \bigcup _{h\in \Gamma } h(L_0\cup L_1)$.

(Problem 5820) Let $W$ be the indicated blue region with the indicated rays and semicircles as its boundary. Show that $W$ is a connected component of $\H \setminus \bigcup _{h\in \Gamma } h(L_0\cup L_1)$.

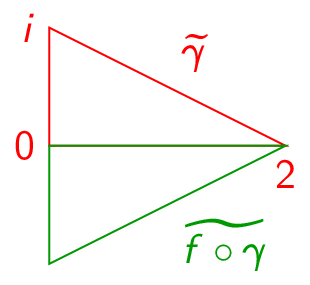
(Problem 5830) Let $V$ be the translation of $W$ leftward by one unit. Show that $V=h(W)$ for some $h\in \Gamma $.

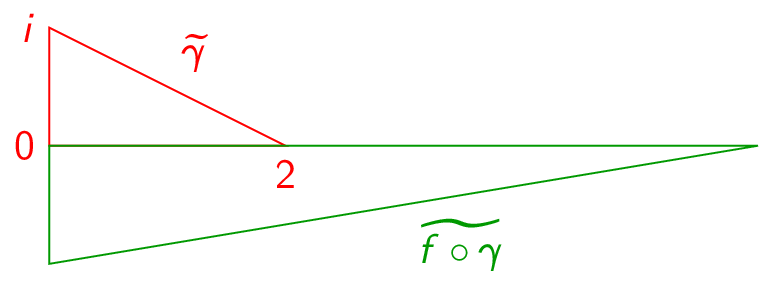
(Problem 5840) Let $U$ be a connected component of $\H \setminus \bigcup _{h\in \Gamma } h(L_0\cup L_1)$. Show that $U=h(W)$ for some $h\in \Gamma $.

(Problem 5850) Suppose that $h\in \Gamma $ and that $h(W)=W$. Show that $h$ must be the identity.

10.5. The Elliptic Modular Function

Recall [Theorem 10.5.4]: There is a function $\lambda :\H \to \C $ (called the modular function) and a nontrivial subgroup $\Gamma $ of $G$ with the following properties.

Theorem 13.2.3. (Carthéodory). Let $\gamma :[0,1]\to \C $ be a simple closed curves. Let $\Omega $ be the bounded component of $\C \setminus \gamma ([0,1])$; by the Jordan curve theorem, there is exactly one such connected component. Clearly $\Omega $ is a simply connected nonempty open proper subset of $\C $.

Then any Riemann map $\Phi :\Omega \to \D $ extends continuously to a bijection from $\overline \Omega $ to $\overline \D $.

(Problem 5870) Let $\Omega $ be the open right half of $W$. Show that there is a continuous bijection $\varphi :\overline \Omega \to \overline \H $ such that $\varphi \big \vert _\Omega $ is a holomorphic bijection $\varphi :\Omega \to \H $. Show that we may furthermore require that $\varphi (1/2)=0$ and $\varphi (1)=1$.

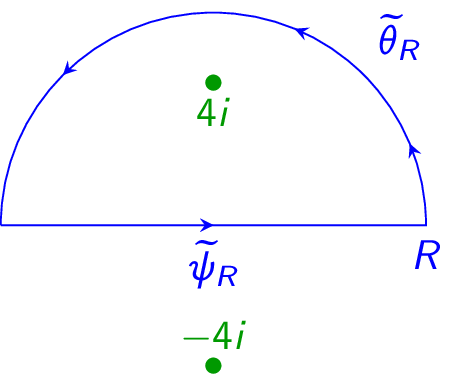
(Problem 5880) Show that there is a continuous function $\psi :\overline W\to \C $, holomorphic in $W$, such that $\psi (z)=\varphi (z)$ for all $z\in \Omega $. Show that $\psi $ is a holomorphic bijection from $W$ to $\C \setminus [0,\infty )$ and that $\psi (\H \cap \overline W)=\C \setminus \{0,1\}$.

(Problem 5890) Let $z$, $w\in \overline W$. Show that $\psi (z)=\psi (w)$ if and only if $h(z)=w$ for some $h\in \Gamma $.

(Problem 5900) Define $\lambda (z)=\psi (h(z))$, where $h\in \Gamma $ satisfies $h(z)\in \overline W$. Show that $\lambda $ is well defined and continuous on $\H $ and prove parts (b) and (f) of Theorem 10.5.4.

[Chapter 3, Problem 6] If $f$ is continuous on $D(P,r)$ and is holomorphic in $D(P,r)\setminus S$, where $S$ is a line or circle passing through $P$, then $f$ is holomorphic on all of $S$.

(Problem 5910) Prove part (d) of Theorem 10.5.4; that is, show that $\lambda $ is holomorphic on $\H $.

(Problem 5911) Prove part (c) of Theorem 10.5.4; that is, show that if $\lambda (z)=\lambda (w)$ then $z=h(w)$ for some $f\in \Gamma $.

Contents

1.1. Elementary Properties of the Complex Numbers

1.2. Real Analysis

1.2. Further Properties of the Complex Numbers

1.3. Real Analysis

1.3. Complex Polynomials

1.3. The complex derivatives \(\p {z}\) and \(\p {\bar z}\)

1.4. Holomorphic Functions, the Cauchy-Riemann Equations, and Harmonic Functions

1.5. Real Analysis

1.5. Real and Holomorphic Antiderivatives

2.1. Real Analysis

2.1. Real and Complex Line Integrals

2.2. Real Analysis

2.2. Complex Differentiability and Conformality

2.3. Real Analysis

2.3. Antiderivatives Revisited

2.4. Real Analysis

2.4. The Cauchy Integral Formula and the Cauchy Integral Theorem

2.5. The Cauchy Integral Formula: Some Examples

2.4. The Cauchy Integral Formula and the Cauchy Integral Theorem

Coda: Change of variables

2.6. An Introduction to the Cauchy Integral Theorem and the Cauchy Integral Formula for More General Curves

3.1. Differentiability Properties of Holomorphic Functions

Notes on Homework 5

3.1. Real Analysis

3.1. Morera’s theorem

3.2. Real Analysis

3.2. Complex Power Series

3.3. The Power Series Expansion for a Holomorphic Function

3.4. The Cauchy Estimates and Liouville’s Theorem

3.5. Uniform Limits of Holomorphic Functions

3.6. Real Analysis

3.6. The Zeros of a Holomorphic Function

4.1. The Behavior of a Holomorphic Function Near an Isolated Singularity

4.2. Convergence of Laurent series

4.3. Existence of Laurent Expansions

4.3. The Laurent series near an isolated singularity

4.4. Examples of Laurent Expansions

4.5. Real Analysis

4.5. The index of a curve around a point

4.5. The Calculus of Residues

4.6. Applications of the Calculus of Residues to the Calculation of Definite Integrals and Sums

4.6. Calculation of Sums

4.7. Real analysis

4.7. Meromorphic Functions

4.7. Singularities at Infinity

5.1. Counting Zeros and Poles

5.2. The Local Geometry of Holomorphic Functions

5.2. Real Analysis

5.2. The Open Mapping Theorem

5.2. Simple points, multiple points, and inverses

5.3. Further Results on the Zeros of Holomorphic Functions: Rouché’s theorem

5.4. The Maximum Modulus Principle

5.3. Further Results on the Zeros of Holomorphic Functions: Hurwitz’s theorem

5.5. The Schwarz Lemma

5.5. Möbius transformations

5.5. The Schwarz-Pick lemma

6.3. Linear Fractional Transformations

6. Holomorphic functions as Geometric Mappings

6.1. Biholomorphic self-maps of \(\C \)

6.2. Real analysis

6.2. Biholomorphic self-maps of \(\D \)

6.3. Bimeromorphic self-maps of \(\C \cup \{\infty \}\)

6.4. The Riemann Mapping Theorem

6.5. Real Analysis

6.5. Normal Families

6.7. The Proof of the Analytic Form of the Riemann Mapping Theorem

7.1. Basic Properties of Harmonic Functions

7.2. The Maximum Principle

7.2. The Mean Value Property

7.3. The Poisson Integral Formula

7.4. Real Analysis

7.4. Regularity of Harmonic Functions

7.5. The Schwarz Reflection Principle

7.6. Real Analysis

7.6. Harnack’s Principle

7.7. Real Analysis

7.7. Subharmonic Functions

7.7. The Dirichlet Problem

7.8. Real Analysis